论文阅读笔记四十七:Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression(CVPR2019)

论文原址:https://arxiv.org/pdf/1902.09630.pdf
github:https://github.com/generalized-iou
摘要
在目标检测的评测体系中,IoU是最流行的评价准则。然而,在对边界框的参数进行优化时,常用到距离损失,而按照IOU的标准则是取其最大值,二者之间是有一定差别的。对一个标准进行优化的目标函数是其标准本身。比如,对于2D的坐标对齐的边界框,可以直接使用IoU作为回归损失。然而,该方法存在一个弊端,就是当两个边界框不发生重叠时,IoU对损失的贡献度为0。本文通过定义了一个广义新的损失及评价标准来解决IoU上述问题的不足,即generalized IoU(GIoU),将GIoU潜入当前较好的目标检测模型中作为损失,在Pascal VOC及MS COCO数据集上有了较大的提升。
介绍
在2D/3D的计算机视觉任务中,边界框回归时最基本的一个组件。像目标定位,多目标检测,目标追踪及实例分割等都依赖于准确的边界框回归。该领域趋于通过利用较好的backbone或者更好的策略来提取局部特征的深度学习网络来提升其性能,然而,有一点被人们所忽略的是可以用基于IoU的评价计算机制替换常规的L1,L2损失函数。
IoU也称做Jaccard index,是比较两个任意形状物体相似度最常用的评价标准。IoU编码比较两个边界框的像宽度,长度及位置等形状属性为局部属性,然后,基于正则化机制来关注二者的区域。IoU具有尺寸不变性,基于此机制可以进行目标检测,分割及追踪等。
然而,在2D/3D空间上定义两个边界框参数表示的常规损失如Ln等使其值最小与通过优化来提高IoU的值,二者之间的并没有太大的关联,如下图所示。黑色的框为预测的框,绿色框为ground truth,每个框由一对角点(左上角及右下角)确定,本文固定这两个边界框中的一个角点之间的距离,比如两个框的左下角的角点之间的L2距离固定,则若预测框的第二个角点总是位于以ground truth第二个角点为圆心的圆上,则二者之间的距离是相同的,但是反观IoU,其值的变化范围还是很大的。
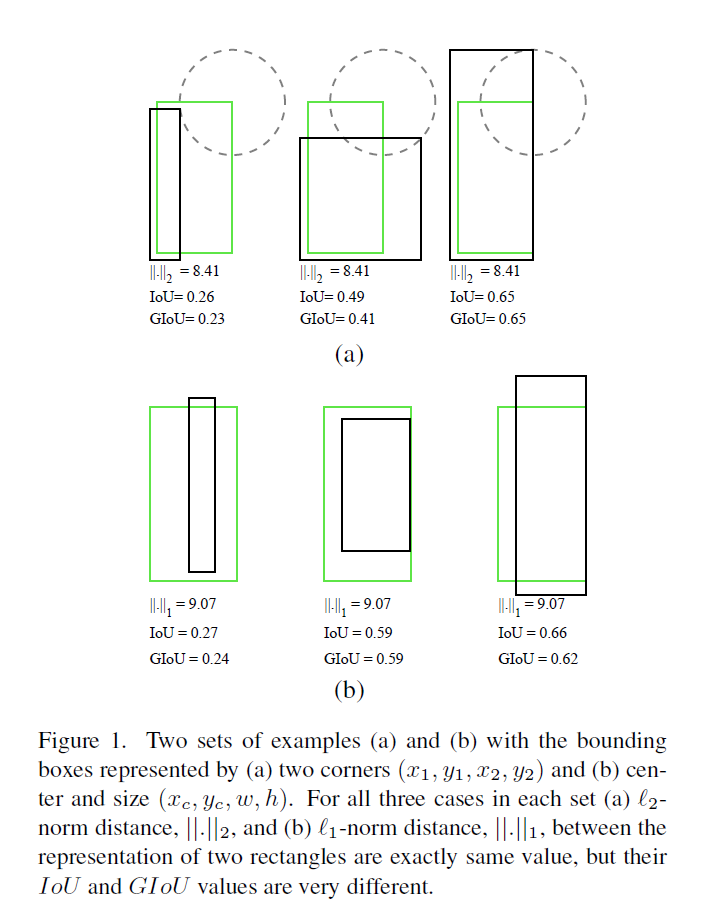
一种直观上的感受就是,找到了像损失这样的局部最优解对与IoU的局部最优并不产生任何影响。同时,与IoU不同的是,ln-norm目标的构建是基于对于问题的尺寸问题敏感的参数表示。比如,一系列框中具有相同层次的重叠率但由于角度问题形成不同的尺寸,进而得到不同的目标值。另外,不同类型参数表示之间存在正则化上的不足。比如,增加参数或者引入新的维度会增加模型的复杂度,因此一些经典的检测方法引入anchor这种先验猜想,同时定义了一个非线性表示来弥补尺寸的变化。虽然有了上述的改进,但IoU与回归损失二者的优化仍存在较大的差别。
本文研究了两个轴对齐框的IoU的计算,提出了IoU可以进行反向传播,并用于目标函数的优化。IoU同时作为标准及损失存在两个问题:
(1)如果两个目标物未发生重叠,则IoU的值为0,也就无法反应出二者之间的形状差异,同时,IoU作为损失,其梯度将变为0,进而无法进行优化。
(2)IoU无法正确区分不同对齐方式的两个目标为,换言之,不同方位的两个目标物,其IoU的值可能会是相同的,如下图,因此,IoU的值无法反应两个目标物实际的重叠度。
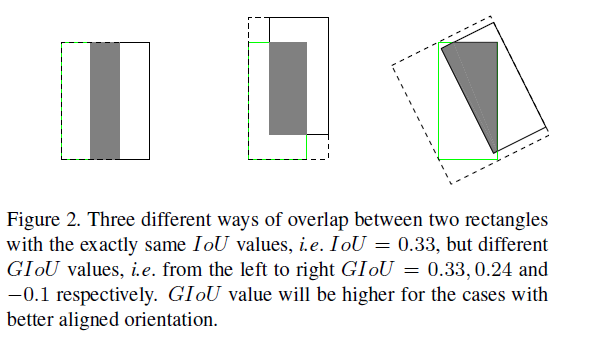
本文通过将IoU扩展至非重叠的情形。主要概括如下:
(a)遵从IoU相同的定义,将两个边界框的尺寸信息进行编码作为区域属性。
(b)保持IoU的尺寸不变性。
(c)增加重叠目标物下二者IoU的相关度。
相关工作
目标检测准确率的评估:IoU在目标检测中用于判断预测出的框是正样本还是负样本。当用于准确率的评估时,必须选择一个值作为阈值,比如VOC中的mAP需要固定IoU的值比如为0.5 。然而,对于不同的方法,IoU值的任意选择并不会完全影响定位效果。当IoU的值超过一定的值后,定位的准确率是相同的。为了降低对IoU阈值的敏感性,MS COCO取不同阈值IoU下mAP的均值。
边界框的表示及其损失:在2D目标检测任务中,边界框参数的学习是至关重要的。YOLOv1通过预测边界框大小的开方来对边界框进行回归从而弥补尺寸的敏感性。R-CNN通过对基于Selective Search方法得到的先验框位置预测及偏移量大小的预测来对边界框进行参数化表示。进而通过对偏移量进行log-space变换来减弱尺寸对表示的敏感性。基于L2-norm的目标函数如MSE损失,作为优化目标。Fast R-CNN提出用L1-smooth损失来学习更鲁棒的外形信息。后来又引入了anchor等先验框,但其存在明显的类别不平衡问题,因此,很难进行训练,因此引入了Focal Loss来进行弥补。
基于近似值来对IoU进行优化:在语义分割中,基于近似函数或者surrogate loss来对IoU进行优化。在目标检测中存在不重叠情形下IoU的优化问题,本文提出的G-IoU将IoU直接作为目标检测任务中损失函数的一部分进行优化。
Generalized Intersection over Union
IoU定义如下

IoU的两个优点:
(1)IoU作为距离,![]() 其值满足metric的所有属性,比如非负性,不可区分性,对称性及三角不等式。
其值满足metric的所有属性,比如非负性,不可区分性,对称性及三角不等式。
(1)IoU对于问题的尺寸具有不变性。任意形状的两个物体A,B之间的相似性与其尺寸无关。
IoU的两个缺点:
(1)如果两个物体A,B不发生重叠,IoU不起任何作用。
(2)只要两个不同的轴对齐框的相交区域相同,IoU的值相同的,因此,IoU并不反映两个框重叠的方式,如上图2所示。
G-IoU:首先对于任意的两个形状A,B,找到可以包含A,B的最小凸区域C。为了比较两个形状确定的几何体,C的类型可以是相同的,比如A,B都为椭圆,则C可以为包含A,B的最小椭圆。然后,计算抛除A,B后C剩余区域与C整个区域的比值。该方法可以更多的关注A,B之间的空白区域。最后,G-IoU可以有IoU减去前面的值得到。算法如下:

GIou作为一个新的metric有如下特性:
1. 与IoU相似,作为距离,![]()
![]() 保留前文IoU的所有距离性质。
保留前文IoU的所有距离性质。
2. GIoU对于尺寸具有不变性。
3. GIoU总是IoU的一个下界,![]() 当A,B之间相似度很高时,取等号。
当A,B之间相似度很高时,取等号。
![]()
![]()

5. 与IoU不同的是,GIoU不只是关注重叠区域,而且更关注两个区域是如何重叠的。
GIoU as Loss for Bounding Box Regression
在目标检测中,所有的框都为矩形框,因此,可以为计算最小包含区域提供了可行性,利用其坐标的最小及最大函数进行求取。在包含不相交情形的所有情况,GIoU都是存在梯度值的,此外,在较高的IoU下GIoU与IoU具有强烈的相关性,如下图所示。
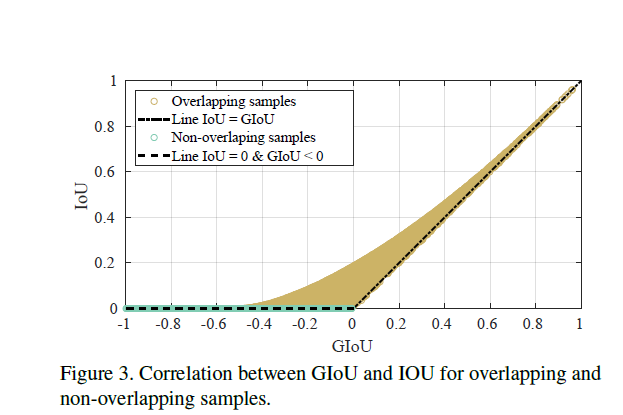
Loss Stability: 本文研究对于预测的输出,是否存在极端情况使损失不稳定或者不存在定义。
ground truth的边界管Bg是大于0的,同理,Ag也大于0,下列算法中的(1),(4)分别保证了预测的区域及相交区域均为大于0的。因此,对于任意的预测值![]() ,保证IoU的分母不为0.同时,union总比相交区域大。
,保证IoU的分母不为0.同时,union总比相交区域大。

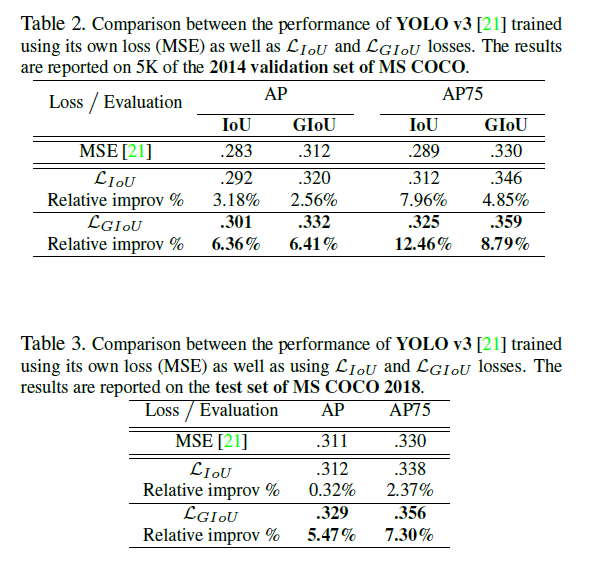
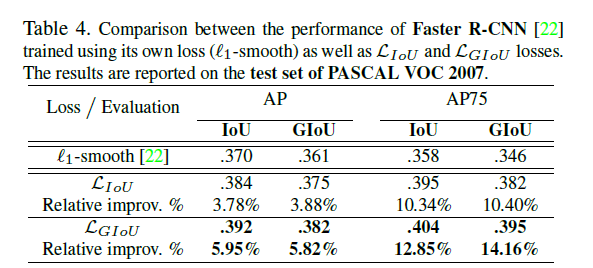
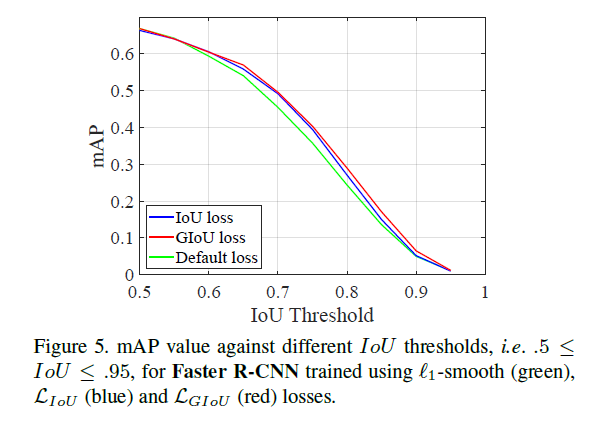
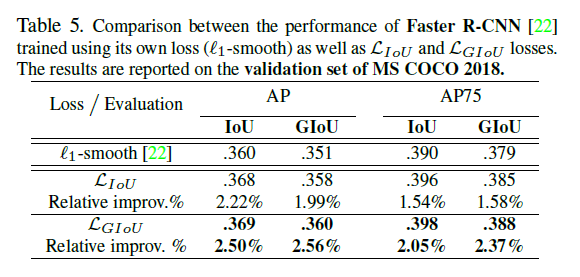
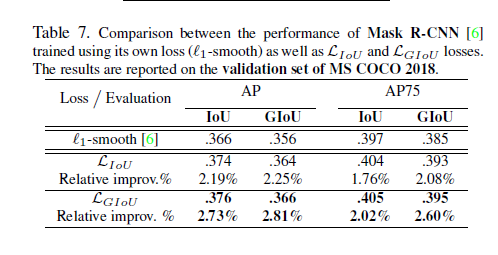
实验
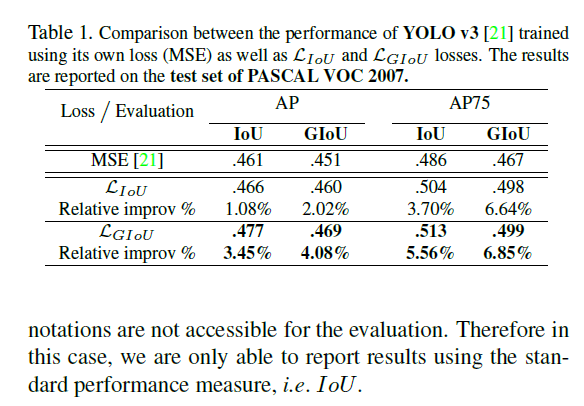


Reference
[1] H. Alhaija, S. Mustikovela, L. Mescheder, A. Geiger, and C. Rother. Augmented reality meets computer vision: Efficient
data generation for urban driving scenes. International Journal of Computer Vision (IJCV), 2018. 1
[2] M. Cordts, M. Omran, S. Ramos, T. Rehfeld, M. Enzweiler,R. Benenson, U. Franke, S. Roth, and B. Schiele. The
cityscapes dataset for semantic urban scene understanding.In Proc. of the IEEE Conference on Computer Vision and
Pattern Recognition (CVPR), 2016. 1
[3] J. Dai, Y. Li, K. He, and J. Sun. R-fcn: Object detection via region-based fully convolutional networks. In Advances
in neural information processing systems, pages 379–387,2016. 3
[4] M. Everingham, L. Van Gool, C. K. I.Williams, J.Winn, and A. Zisserman. The pascal visual object classes (voc) challenge.International Journal of Computer Vision, 88(2):303–338, June 2010. 1, 2, 5



 浙公网安备 33010602011771号
浙公网安备 33010602011771号