查找算法之插值查找

参考

1. 七大查找算法 | 博客园

 

主要思想

二分查找算法是傻瓜式的将待查找序列一分为二进行查找，直到找到或者查找失败。插值查找算法，是针对待查找序列均匀分布特点、结合二分查找算法进行改进的一种自适应查找算法。

一般的，二分查找范围一个很重要的点

middle = (left + right)/2

而插值查找，可根据目标元素在待查找序列中的到边界值的大小来估算到边界的距离，通过估算的距离快速缩小目标所在序列的范围，即

middle = left + (target - a[left]) / (a[right] - a[left]) * (right - left)， 当然有前提条件left < right, 不能取等号。

 

先决条件

与二分查找算法先决条件一样，可以理解为二分查找算法的优化

1. 待查存储在顺序表中（数组，而非链表）；

2. 待查顺序表有序（递增，递减都可以，相邻元素相等也可以）

 

例程

 递增序列a = [3, 6, 9, 12, 20, 25, 30 ,36]，

1. 待查找目标t=25 ，正常结果是返回5

2. 待查找目标t=11，正常结果是查找失败（返回-1）

 

 

 

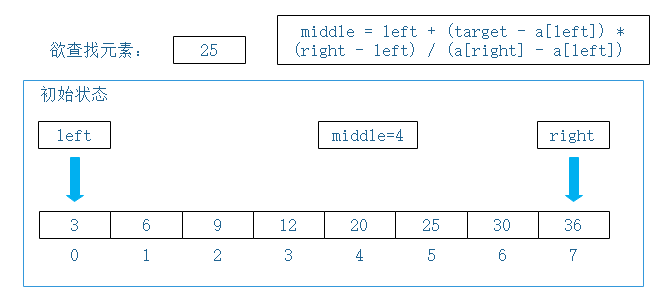
网上流行的代码：乍一看是没什么问题，实际上，初始情况或者中间计算过程可能存在mid < left或者mid>right的情况。这显然不合理，因为没有在left~right正常范围进行查找。

#error realization
def interpolation_search(a, target):
    left = 0
    right = len(a) - 1

    print 'left = %d, right = %d'%(left, right)

    while left < right:
        middle = left + (target - a[left]) * (right - left) / (a[right] - a[left])

        print 'left=%d, middle=%d, right=%d'%(left, middle, right)
        if a[middle] < target:
            left = middle + 1
        elif a[middle] > target:
            right = middle - 1
        else:
            print 'sucess to find out the target'
            return middle

    if left == right:
        middle = left
        if a[middle]  == target:
            print 'sucess to find out the target'
            return middle

    print 'fail to find out the target'
    return -1


data = [3, 6, 9, 12, 20, 25, 30,36]
print interpolation_search(data, 25)
print interpolation_search(data, 11) #result in endless loop

 

 如何解决middle超界限的问题？

假设第n步，出现middle(n) < left(n)，也就意味着a[middle(n)] < a[left(n)]（因为a是递增序列）；

那么在前一步，a[middle(n-1)] > a[left(n-1)] ， 导致left_n=middle(n-1) + 1 > middle(n-1)，

进而重复到middle(n) = left(n) + (target - a[left(n)]) / (a[right(n)] - a[left(n)]) * (right(n) - left(n)) < left(n)；

 

 不妨在第n步，添加对middle(n), left(n)的判断，如果发现middle(n) < left(n)及时终止循环，返回查找失败状态。

#modified realization
def interpolation_search(a, target):
    left = 0
    right = len(a) - 1

    print 'left = %d, right = %d'%(left, right)

    while left < right:
        middle = left + (target - a[left]) * (right - left) / (a[right] - a[left])

        print 'left=%d, middle=%d, right=%d'%(left, middle, right)

        if middle >= left and middle <= right:
            if a[middle] < target:
                left = middle + 1
            elif a[middle] > target:
                right = middle - 1
            else:
                print 'sucess to find out the target'
                return middle
        else:
            print 'fail to find out the target'
            return -1

    if left == right:
        middle = left
        if a[middle]  == target:
            print 'sucess to find out the target'
            return middle

    print 'fail to find out the target'
    return -1


data = [3, 6, 9, 12, 20, 25, 30,36]
print interpolation_search(data, 25)
print interpolation_search(data, 11)

 

运行结果：

left = 0, right = 7
left=0, middle=4, right=7
left=5, middle=5, right=7
sucess to find out the target
5
left = 0, right = 7
left=0, middle=1, right=7
left=2, middle=2, right=7
left=3, middle=2, right=7
fail to find out the target
-1