计算机图形:三角形光栅化
三角形光栅化
光栅化:将几何数据经一系列变换,最终转换为像素,而在屏幕上显示的过程.
直线光栅化:在2D屏幕上,对两端点间插值,绘制一条直线(段). 常用中点算法和Bresenham算法,Bresensham算法参见Bresenham画直线算法(所有斜率).
类似地,视口变换后,要在2D屏幕上绘制\(\Delta \bm{abc}\),顶点坐标\(a(x_0,y_0),b(x_1,y_1),c(x_2,y_2)\). 三角形的绘制,需要用顶点颜色或其他属性插值,即重心坐标插值(详见计算机图形:三角形及重心空间).
假设三顶点颜色\(\bm{c_0,c_1,c_2}\),那么三角形中任一点\(p(x,y)\)重心插值坐标为\((α,β,γ)\),颜色为:
tips: Gouraud明暗处理中,用这种方法对光强进行插值.
绘制三角形轮廓
可用中点算法(midpoint algorithm)绘制三角形轮廓.
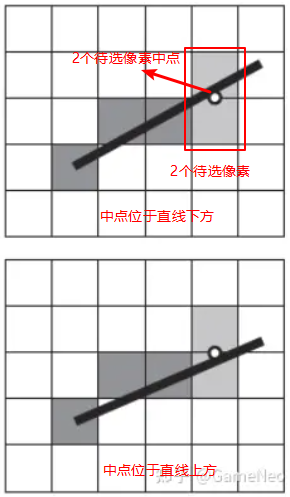
图片from 计算机是怎么画线的?中点算法与Bresenham算法
中点算法思想:以斜率>0为例,画直线要确定下一像素时,将位于右侧和右上侧的2个待选像素中心点的中点代入直线方程,根据中点位于该直线的上方 or 下方决定下个像素. 当中点位于上侧,说明直线靠近右侧像素;反之,说明直线靠近右上侧像素.
直线公式推导
\(△abc\)中,直线\(ab,bc,ac\)方程:
\[\begin{aligned} f_{ab}(x,y)&=(y_a-y_b)x+(x_b-x_a)y+x_ay_b-x_by_a\\ f_{bc}(x,y)&=(y_b-y_c)x+(x_c-x_b)y+x_by_c-x_cy_b\\ f_{ac}(x,y)&=(y_c-y_a)x+(x_a-x_c)y+x_cy_a-x_ay_c \end{aligned} \]
以求直线\(bc\)方程\(f_{bc}\)为例.
证:设\(bc:f_{bc}(x,y)=Ax+By+C=0\)
有
∴\((A,B)⊥(x_c-x_b,y_c-y_b)\)
又\((y_b-y_c,x_c-x_b)⊥(x_c-x_b,y_c-y_b)\)
不妨取\((A,B)=(y_b-y_c,x_c-x_b)\),于是
\(f_{bc}(x,y)=(y_b-y_c)x+(x_c-x_b)y+C=0\)
∵\(f_{bc}\)过\(b(x_b,y_b)\)
∴\(f_{bc}(x_b,y_b)=(y_b-y_c)x_b+(x_c-x_b)y_b+C=0\)
∴\(C=x_by_c-x_cy_b\)
∴\(f_{bc}(x,y)=(y_b-y_c)x+(x_c-x_b)y+x_by_c-x_cy_b=0\)
填充三角形内部
总流程:重心坐标 \(\xrightarrow{α,β,γ\in (0,1)?}\) 是否像素绘制\(\xrightarrow{顶点插值颜色}\)像素颜色
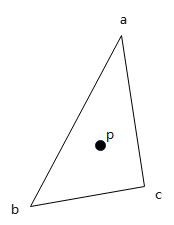
平面上任一点\(p(x,y)\),都能用以三角形三顶点\(\bm{a,b,c}\)为基础的重心坐标表示.
其中,\(A_a,A_b,A_c,A\)分别表示三角形\(pbc,pac,pab,abc\)面积. 由于都是三角形面积比值,可以换算成同底不同高的比值.
该公式可用于颜色等属性插值.
如何判断像素是否位于三角形内?
方法一:通过重心坐标判断.
当像素点的重心坐标\(α,β,γ\in(0,1)\)时,认为像素中心位于三角形内,而避免顺序问题、消除孔洞.
方法二:通过叉积判断.
前面针对平面多边形的奇偶规则和非零环绕数,也适用(见计算机图形:输出图元). 不过,针对三角形,还有更简单的办法.
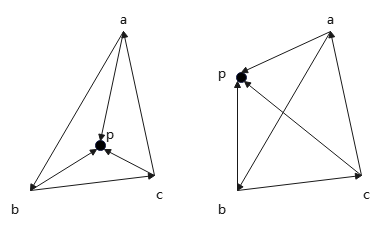
如上图,以逆时针顺序建立\(△abc\).
平面上一点p位于三角形内部时,则叉积\(\overrightarrow{ab}\times \overrightarrow{ap}\)垂直平面向外(+z轴方向),同样地,\(\overrightarrow{bc}\times \overrightarrow{bp}, \overrightarrow{ca}\times \overrightarrow{cp}\)也是+z轴方向.
p位于三角形外部时,\(\overrightarrow{ab}\times \overrightarrow{ap}\)为-z轴方向,\(\overrightarrow{bc}\times \overrightarrow{bp}, \overrightarrow{ca}\times \overrightarrow{cp}\)为+z轴方向.
i.e. 可通过叉积判断点p是否在三角形内部:
1)当\(\overrightarrow{ab}\times \overrightarrow{ap}, \overrightarrow{bc}\times \overrightarrow{bp}, \overrightarrow{ca}\times \overrightarrow{cp}\)符号相同时,p在内部;否则,在外部.
2)当符号为0时,p在对应的三角形边上.
三角形内部像素的颜色插值
如何利用重心插值,填充三角形内部像素?
遍历屏幕所有像素点,当点位于三角形内部时,通过颜色插值进行绘制. 实践中,为减少要遍历的像素点,可用三顶点构造一个边界矩形,将检索范围限制在矩形内.
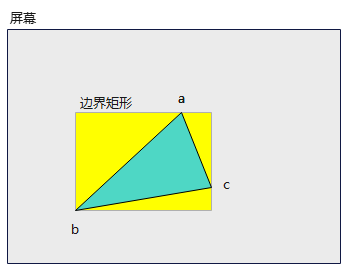
算法如下:
// a(xa,ya),b(xb,yb),c(xc,yc) consits of a 2D triangle, including color property
xmin = floor(x[i]); // 向下取整
xmax = ceiling(x[i]); // 向上取整
ymin = floor(y[i]);
ymax = ceiling(y[i]);
for (y = ymin; y <= ymax; y++) {
for (x = xmin ; x <= xmax; x++) {
alpha = f_bc(x, y) / f_bc(xa, ya);
beta = f_ac(x, y) / f_ac(xb, yb);
gamma = f_ab(x, y) / f_ab(xc, yc);
if (alpha > 0 && beta > 0 && gamma > 0) {
color = alpha * a + beta * b + gamma * c; // color of pixel(x,y)
drawpixel(x, y, color);
}
}
}
\(f_{ab},f_{bc},f_{ac}\)分别表示直线\(ab,bc,ac\),对应方程:
为什么\(α=f_{bc}(x_p,y_p)/f_{bc}(x_a,y_a)\)?
∵\(p(x_p,y_p)\)在\(△abc\)中的重心坐标:
其中,\(A,B,C\)是\(△abc\)三个顶点.
而
同理,可得
重心坐标及点到直线距离(\(d_{p,bc},d_{a,bc}\)),推导可参见计算机图形:三角形及重心空间
问题: 为什么循环体内只测试\(α,β,γ>0\),而不是验证\(\in (0,1)\)?
因为\(α+β+γ=1\),如果3者都>0,那么都位于区间\((0,1)\).
- 增量法节省计算量
绘制直线时,考虑到相邻像素,有以下关系:
如此,只需1次加法,就能求出\(f(x,y+1),f(x+1,y)\),从而减少求\(α.β,γ\)时间.
处理公共边界
如果一个像素中心位于2个三角形的公共边,该如何处理?
有3种策略:
-
下策:不绘制该像素,但是会在2个三角形之间形成孔洞.
-
中策:2个三角形都绘制该像素,但如果三角形是透明的,会造成双重着色.
-
上侧:属于哪个三角形不重要,选择明确即可.
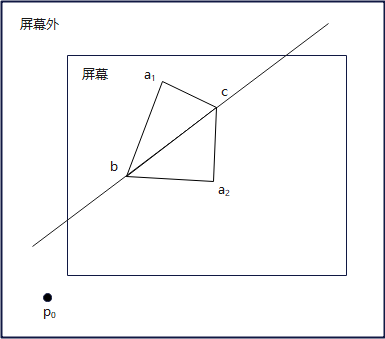
一种简单的选择方法,是找一个屏幕外的点,比如\(p_0(-1,-1)\),通常认为屏幕外的点不在直线上.
\(f_{bc}(\bm{p_0})\cdot f_{bc}(\bm{{a_1}})<0\),表明\(\bm{p_0},\bm{a_1}\)在直线bc不同侧;
\(f_{bc}(\bm{p_0})\cdot f_{bc}(\bm{{a_2}})<0\),表明\(\bm{p_0},\bm{a_2}\)在直线bc同侧;
那么,选择\(△a_2bc\)绘制公共边bc.
当\(α=0\)时, \(f_{bc}(x,y)=0\),代表p在bc上;
当\(β=0\)时, \(f_{ac}(x,y)=0\),代表p在ac上;
当\(γ=0\)时, \(f_{ab}(x,y)=0\),代表p在ab上.
算法如下:
// a(xa,ya),b(xb,yb),c(xc,yc) consits of a 2D triangle, including color property
xmin = floor(x[i]);
xmax = ceiling(x[i]);
ymin = floor(y[i]);
ymax = ceiling(y[i]);
p0 = (-1, -1);
f_alpha = f_bc(xa, ya);
f_beta = f_ac(xb, yb);
f_gamma = f_ab(xc, yc);
for (y = ymin; y <= ymax; y++) {
for (x = xmin ; x <= xmax; x++) {
alpha = f_bc(x, y) / f_alpha;
beta = f_ac(x, y) / f_beta;
gamma = f_ab(x, y) / f_gamma;
if (alpha >= 0 && belta >= 0 && gamma >= 0 ) {
if ((alpha > 0 || f_alpha * f_bc(p0.x, p0.y))
&& (beta > 0 || f_beta * f_ac(p0.x, p0.y))
&& (gamma > 0 || f_gamma * f_ab(p0.x, p0.y))
) {
color = alpha * a + beta * b + gamma * c; // color of pixel(x,y)
drawpixel(x, y, color);
}
}
}
}
这样做的好处:只需在当前三角形,判断每个顶点是否与\(p_0\)一样,在对边的同侧,而无需知道是否有公共边.
当然,也存在缺点:\(p_0\)可能在三角形某条边所在直线,从而无法判定该边应在哪个三角形中绘制. 不过,大多数情况,\(p_0\)都能起到作用.
待解决疑问:有没有一种可能性,边bc不是公共边,因为\(\bm{a},\bm{p_0}\)不在同侧,因此不算在当前三角形内绘制,从而导致没有绘制?
异常处理
对于退化三角形,三角形退化为一条直线,如\(f_α=0\),即a到bc距离为0,即a在bc上. 此时,求α的除数为0,显然不行.
如何处理?
阻止异常数据. 在算法作除法前,先测试是否为退化三角形,如果是,就当成直线绘制;如果不是,就继续. 当然,浮点数的计算误差也应该考虑在内.
裁剪
简单将图元变换到屏幕空间,并且对其光栅化并不能完全工作,因为图元可能中观察体(view volume)外,特别是在眼睛后面的图元,被光栅化后可能导致错误结果. 因此,需要进行裁剪.
裁剪(clipping),就是用一个几何体剪切另一个,剔除掉观察体以外的部分. 例如,用平面\(x=0\)剪切三角形,如果三角形顶点的x坐标符号不完全相同,那么平面会将三角形切成2个部分.
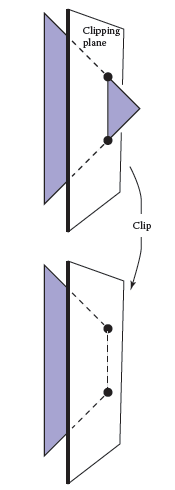
两种最常用的裁剪方法:
1)世界坐标系中,用视锥体的6个平面(近、远、左、右、上、下裁剪面);
2)在齐次除法之前的4D变换空间(即Clip Space)中.
对于每个三角形,以下方法均可有效实现这两种可能(J.Blinn, 1996):
for each of six plances do
if (triangle entirely outside of plane) then
break (triangle is not visible)
else if (triangle spans plane) then
clip triangle
if (quadrilateral is left) then
break into two triangles
下面描述这2个方法:
变换前裁剪
对于1),重要的是6个平面方程. 6个平面方程是什么?
因为方程对于单个图像中渲染的所有三角形都是一样的,所以不需要非常高效地计算. 观察体的8个顶点:
于是,可从观察体8个顶点得出6个平面方程.
注意:没有指明一定是表面垂直于坐标轴的对称棱台观察体.
齐次坐标中裁剪
对于2),通常在齐次除法之前的齐次空间(Clip Space)中进行裁剪. 这里,视锥体是4D的,由3D体积(超平面)界定. 这些超平面是:
平面方程很简单,效率优于1). 通过将视锥体\([l,r]\times [b,t]\times [f,n]\)变换到\([-1,1]^3\),仍然可进一步提高效率.
裁剪平面
不论选择1),还是2),都必须裁剪平面. 通过点\(q\)、法向量\(\bm{n}\)的平面的隐式方程:
常写作:
假如我们有线段\(ab\),测试点\(a,b\)以确定它们是否位于平面\(f(\bm{p})\)的两侧,方法:检查\(f(\bm{a}),f(\bm{b})\)符号是否不同. \(f(\bm{p})<0\)定义为“平面内部”;\(f(\bm{p})>0\)定义为“平面外部”.
如果线段与平面相交,可通过代入参数方程求交点. 直线\(ab\)上一点p的参数方程:
代入平面方程\(f(\bm{p})=0\),得
这样,就能求出线段\(ab\)与平面交点,并进一步缩短线段.
参考
[1] Marschner S , Shirley P , Ashikhmin M ,et al.Fundamentals of computer graphics, fourth edition[J].A. K. Peters, Ltd. 2015.
[2] 计算机图形学——三角形光栅化



 浙公网安备 33010602011771号
浙公网安备 33010602011771号