导数、偏导数、方向导数与梯度

目录

• 导数
• 偏导数
• 全微分
• 方向导数
• 梯度
• 参考

导数

导数是一元函数的概念.

函数\(y=f(x)\)在点\(x_0\)的某个邻域内有定义，自变量\(x\)在\(x_0\)处每取得\(\Delta x\)增量，因变量\(y\)取得\(\Delta y=f(x_0+\Delta x)-f(x_0)\)增量.

如果\(\Delta x\to 0\)时，极限\(\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}\)存在，则称\(y=f(x)\)在\(x_0\)处可导，该极限称为\(f(x)\)在\(x_0\)处导数，记为\(f'(x_0),y'\mid_{x=x_0}\)或\(\frac{df(x)}{dx}\mid_{x=x_0}\).

\[f'(x_0)=\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \]

另2种等价写法：

\[\begin{aligned} f'(x_0)&=\lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}\\ f'(x_0)&=\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} \end{aligned} \]

如果\(y=f(x)\)在定义域内都可导，则可记：

\[f'(x),y', \space or \space \frac{df(x)}{dx} \]

导数几何意义：函数的变化率、切线斜率.

偏导数

偏导数是多元函数的概念. 定义偏导数时，只有1个自变量变化，固定其他自变量，进而研究因变量的变化.

以二元函数\(z=f(x,y)\)为例：
设函数\(z=f(x,y)\)在点\((x_0,y_0)\)的某一邻域内有定义，\(y\)固定在\(y_0\)、\(x\)在\(x_0\)处增量\(\Delta x\)，那么函数增量：

\[\Delta z = f(x_0+\Delta x, y_0)-f(x_0, y_0) \]

如果极限

\[\lim\limits_{\Delta x\to 0}\frac{\Delta z}{\Delta x}=\lim\limits_{\Delta x\to 0}\frac{f(x_0+\Delta x, y_0)-f(x_0, y_0)}{\Delta x} \]

存在，则称该极限为\(z=f(x,y)\)在点\((x_0,y_0)\)处对\(x\)的偏导数.

该偏导数3种记法：

\[\frac{\partial z}{\partial x}\mid_{\begin{aligned}x=x_0\\y=y_0\end{aligned}}, \frac{\partial f}{\partial x}\mid_{\begin{aligned}x=x_0\\y=y_0\end{aligned}}\space or \space f_x(x_0,y_0) \]

类似，\(z=f(x,y)\)在点\((x_0,y_0)\)处对y的偏导数：

\[f_y(x_0,y_0)=\lim\limits_{\Delta y\to 0}\frac{\Delta z}{\Delta y}=\lim\limits_{\Delta y\to 0}\frac{f(x_0, y_0+\Delta y)-f(x_0, y_0)}{\Delta y} \]

如果\(z=f(x,y)\)在定义域内对\(x\)的偏导数都存在，则可写作：

\[\frac{\partial z}{\partial x},\frac{\partial f}{\partial x}\space or \space f_x(x,y) \]

简写：\(f_x\)

如果\(z=f(x,y)\)在定义域内对\(y\)的偏导数都存在，则可写作：

\[\frac{\partial z}{\partial y},\frac{\partial f}{\partial y}\space or \space f_y(x,y) \]

简写：\(f_y\)

偏导数的几何意义：函数沿着坐标轴方向的变化率.

全微分

偏导数只让一个自变量变化，固定其他自变量，从而得到变化率；全微分是让所有自变量同时变化，从而得到因变量增量.

以二元函数\(z=f(x,y)\)为例，

\[\begin{aligned} f(x+\Delta x,y)-f(x,y)≈f_x(x,y)\Delta x\\ f(x,y+\Delta y)-f(x,y)≈f_y(x,y)\Delta x\\ \end{aligned} \]

左边叫二元函数对x、y的偏增量，右边叫对x、y的偏微分.

对应自变量x、y变化，可得到全增量：

\[\Delta z = f(x+\Delta x, y+\Delta y)-f(x,y) \]

直接计算全增量\(\Delta z\)较为复杂，故用\(\Delta x, \Delta y\)的线性函数近似替代. 如果\(\Delta z\)能表示成：

\[\Delta z = A\Delta x + B\Delta y + o(ρ) \]

其中，A、B不依赖\(\Delta x, \Delta y\)且仅与x、y有关，\(ρ=\sqrt{(\Delta x)^2+(\Delta y)^2}\)，则称\(z=f(x,y)\)在点\((x,y)\)处可微分，线性函数\(A\Delta x+B\Delta y\)为z在\((x,y)\)处的全微分，记作\(dz\).

\[dz=A\Delta x+B\Delta y \]

如果z在区域D内所有点处都可微分，则称z在D内可微分.

\(z=f(x,y)\)在\((x,y)\)处可微分，则在\((x,y)\)处一定连续.

证：

∵\(\lim\limits_{ρ\to 0}\Delta z = \lim\limits_{ρ\to 0}[A\Delta x + B\Delta y + o(ρ)]= \lim\limits_{(\Delta x,\Delta y)\to 0} [A\Delta x+B\Delta y]+\lim\limits_{ρ\to 0}o(ρ)=0\)

∴\(\lim\limits_{ρ\to 0}[f(x+\Delta x, y+\Delta y)]=\lim\limits_{ρ\to 0}[\Delta z+f(x,y)]=\lim\limits_{ρ\to 0}\Delta z + \lim\limits_{ρ\to 0}f(x,y) = f(x, y)\)

∴\(z=f(x,y)\)在\((x,y)\)处连续

• 全微分与偏导数

定理（必要） 如果\(z=f(x,y)\)在点\((x,y)\)可微分，则\(z=f(x,y)\)在该点处偏导数\(\frac{\partial z}{\partial x}、\frac{\partial z}{\partial y}\)存在，且全微分为：

\[dz=\frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y \]

证：
\(P(x,y)\)处可微分 => P的某个邻域内任一点\(P'(x+\Delta x,y+\Delta y)\)，都有\(\Delta z = A\Delta x + B\Delta y + o(ρ)\)成立

令\(\Delta y=0\)，即\(P'(x+\Delta x,y)\)也成立

∴

\[\begin{aligned} \Delta z &= A\Delta x + o(|\Delta x|)\\ f(x+\Delta x, y)-f(x,y)&=A\Delta x+o(|\Delta x|)\\ \lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x, y)-f(x,y)}{\Delta x}&=A=\frac{\partial z}{\partial x} \end{aligned} \]

同理，

\[B=\frac{\partial z}{\partial y} \]

故

\[dz=A\Delta x + B\Delta y=\frac{\partial z}{\partial x}\Delta x+\frac{\partial z}{\partial y}\Delta y \]

定理（充分） 如果函数\(z=f(x,y)\)的偏导数\(\frac{\partial z}{\partial x}、\frac{\partial z}{\partial y}\)在点\((x,y)\)处连续，则函数在该点可微分.

证：

\[\begin{aligned} \Delta z &= f(x+\Delta x, y+\Delta y)-f(x,y)\\ &=[f(x+\Delta x,y+\Delta y)-f(x,y+\Delta y)]+[f(x,y+\Delta y)-f(x,y)] \end{aligned} \]

由拉格朗日中值定理：如果\(f(x)\)在\([a,b]\)上连续，在\((a,b)\)上可导，那么在\((a,b)\)内至少存在一点\(ξ\)，使得\(f'(ξ)=\frac{f(b)-f(a)}{b-a}\)成立.

而\(z=f(x,y)\)在\((x,y)\)处偏导数存在且连续

∴存在\(θ_1,θ_2\in(0,1)\)使得下式成立：

\[\begin{aligned} f(x+\Delta x,y+\Delta y)-f(x,y+\Delta y)&=f_x(x+θ_1\Delta x,y+\Delta y)\Delta x\\ f(x,y+\Delta y)-f(x,y)&=f_y(x,y+θ_2\Delta y)\Delta y \end{aligned} \]

又

\[\begin{aligned} \lim\limits_{\Delta x\to 0,\Delta y\to 0}\frac{f(x+\Delta x,y+\Delta y)-f(x,y+\Delta y)}{\Delta x} &=f_x(x,y)\\ \implies f(x+\Delta x,y+\Delta y)-f(x,y+\Delta y) &=f_x(x,y)\Delta x+ε_1\Delta x\\ \lim\limits_{\Delta y\to 0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}&=f_y(x,y)\\ \implies f(x,y+\Delta y)-f(x,y)&=f_y(x,y)\Delta y+ε_2\Delta y \end{aligned} \]

其中，\(ε_1\)为\(\Delta x,\Delta y\)的函数，当\(\Delta x\to 0,\Delta y\to 0\)时，\(ε_1\to 0\)；\(ε_2\)为\(\Delta y\)的函数，当\(\Delta y\to 0\)时，\(ε_2\to 0\).

∴

\[\Delta z = f_x(x,y)\Delta x+f_y(x,y)\Delta y+ε_1\Delta x+ε_2\Delta y \]

而

\[|\frac{ε_1\Delta x+ε_2\Delta y}{ρ}|=|\frac{ε_1\Delta x+ε_2\Delta y}{\sqrt{x^2+y^2}}|\le |\frac{ε_1\Delta x}{\sqrt{x^2+y^2}}|+|\frac{ε_2\Delta y}{\sqrt{x^2+y^2}}|\le |ε_1|+|ε_2| \]

i.e. \((\Delta x,\Delta y)\to (0,0)\)时，\(ρ\to 0\)，\(ε_1\Delta x+ε_2\Delta y\to 0\)

综上，\(z=f(x,y)\)在\((x,y)\)处可微分.

方向导数

偏导数是函数沿着坐标轴方向的变化率，但有时，需要沿着任意方向的变化率，这就要用到方向导数.

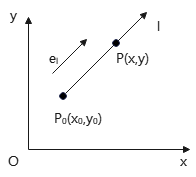
设\(l\)是xOy平面上的一条射线，起点\(P_0(x_0,y_0)\)，同向单位向量\(\bm{e_l}=(\cos α,\cos β)\). 则\(l\)参数方程：

\[\begin{aligned} x&=x_0+t\cos α,\\ y&=y_0+t\cos β,t\ge 0 \end{aligned} \]

设函数\(z=f(x,y)\)在点\(P_0\)的某个邻域\(U(P_0)\)内有定义，该邻域内点\(P(x_0+t\cos α,y_0+t\cos β)\)是\(l\)上一点，那么\(|PP_0|=t\)，函数增量：
\(\Delta z =f(x,y)-f(x_0,y_0)=f(x_0+t\cos α,y_0+t\cos β)-f(x_0,y_0)\)

如果\(P\to P_0(t\to 0^+)\)时，极限：

\[\lim\limits_{t\to 0^+}\frac{\Delta z}{t} \]

存在，则该极限称为函数\(f(x,y)\)在点\(P_0\)沿方向\(l\)的方向导数，即

\[\frac{\partial f}{\partial l}\mid_{(x_0,y_0)}=\lim\limits_{t\to 0^+}\frac{\Delta z}{t} \]

方向导数几何意义：函数在\(P_0\)点处沿着\(l\)方向的变化率.

• 方向导数与偏导数

如果函数在\(P_0\)处偏导数存在，那么函数在\(P_0\)沿着\(\bm{e_l}=(1,0)=(\cos α,\cos β)\)方向的方向导数：

\[\frac{\partial f}{\partial l}\mid_{(x_0,y_0)}=\lim\limits_{t\to 0^+}\frac{\Delta z}{t}=\lim\limits_{t\to 0^+}\frac{f(x_0+t,y_0)-f(x_0,y_0)}{t}=f_x(x_0,y_0) \]

同理，沿着\(\bm{e_l}=(0,1)=(\cos α,\cos β)\)方向的方向导数：

\[\frac{\partial f}{\partial l}\mid_{(x_0,y_0)}=f_y(x_0,y_0) \]

i.e. 偏导数存在时，沿着对应坐标轴方向的方向导数一定存在；反过来，不一定成立.

• 方向导数与全微分

定理 如果函数\(f(x,y)\)在点\(P_0(x_0,y_0)\)可微分，那么函数在该点的方向导数存在，记作\(\frac{\partial f}{\partial l}\mid_{(x_0,y_0)}\)，且有

\[\frac{\partial f}{\partial l}\mid_{(x_0,y_0)}=f_x(x_0,y_0)\cos \alpha + f_y(x_0,y_0)\cos \beta \]

其中，\(\cos \alpha, \cos \beta\)是\(l\)的方向余弦.

tips: 方向余弦：向量\(\bm{e_l}=(\cos \alpha, \cos \beta)\)是\(l\)与同方向的单位向量

证：\(z=f(x,y)\)在\(P_0(x_0,y_0)\)可微分

∴偏导数\(f_x(x_0,y_0),f_y(x_0,y_0)\)存在
∴有

\[\begin{aligned} \Delta z &= A\Delta x+B\Delta y+o(ρ)\\ &=f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+o(\sqrt{(\Delta x)^2+(\Delta y)^2}) \end{aligned} \]

沿着\(l\)方向，

\[\Delta x = t\cos α,\Delta y = t\cos β \]

∴\(ρ=t\)
∴\(\Delta z = f_xt\cos α+f_yt\cos β\)

\[\begin{aligned} \frac{\partial f}{\partial l}\mid_{(x_0,y_0)}&=\lim\limits_{t\to 0^+}\frac{\Delta z}{t}\\ &=\lim\limits_{t\to 0^+}\frac{f_xt\cos α+f_yt\cos β+o(t)}{t}\\ &=f_x(x_0,y_0)\cos α+f_y(x_0,y_0)\cos β \end{aligned} \]

梯度

方向导数是沿着某个方向的变化率，梯度是方向导数中变化率最大的那个方向向量.

设\(f(x,y)\)在平面区域D内具有一阶连续偏导数，对于任一点\(P_0(x_0,y_0)\in D\)，向量

\[f_x(x_0,y_0)\bm{i}+f_y(x_0,y_0)\bm{j} \]

称为\(f(x,y)\)在点\(P_0\)的梯度. 写作：

\[\bm{grad} \space f(x_0,y_0)=▽f(x_0,y_0)=f_x(x_0,y_0)\bm{i}+f_y(x_0,y_0)\bm{j} \]

其中，\(▽=\frac{\partial}{\partial x}\bm{i}+\frac{\partial}{\partial y}\bm{j}\)称为（二维）向量微分算子或Nabla算子，\(▽f=\frac{\partial f}{\partial x}\bm{i}+\frac{\partial f}{\partial y}\bm{j}\). \(\bm{i,j}\)是直角坐标系\(x,y\)轴单位向量

• 梯度与方向导数

如果\(f(x,y)\)在\(P_0(x_0,y_0)\)处可微分，射线\(l\)的方向向量\(\bm{e_l}=(\cos α,\cos β)\)，根据方向导数与全微分关系，有

\[\begin{aligned} \frac{\partial f}{\partial l}\mid_{(x_0,y_0)}&=f_x(x_0,y_0)\cos α+f_y(x_0,y_0)\cos β\\ &=(f_x,f_y)(\cos α,\cos β)\\ &=(f_x,f_y)\cdot \bm{e_l}\\ &=\bm{grad}\space f(x_0,y_0)\cdot \bm{e_l}\\ &=|\bm{grad}\space f(x_0,y_0)|\cos θ \end{aligned} \]

其中，\(θ\)是梯度\(\bm{grad}\space f(x_0,y_0)\)与\(\bm{e_l}\)的夹角.

∵\(f_x(x_0,y_0),f_y(x_0,y_0)\)是确定的
∴\(|\bm{grad}\space f(x_0,y_0)|\)大小确定
∴方向导数\(\frac{\partial f}{\partial l}\mid_{(x_0,y_0)}\)大小取决于\(θ\)大小

1. \(θ=0\)时，即\(\bm{e_l}\)与\(\bm{grad}\space f(x_0,y_0)\)同向，\(f(x,y)\)增加最快，函数在该方向的方向导数达到最大值\(|\bm{grad}\space f(x_0,y_0)|\).

2. \(θ=π\)时，反向，\(f(x,y)\)减少最快，方向导数达到最小值\(-|\bm{grad}\space f(x_0,y_0)|\).

3. \(θ=\frac{π}{2}\)时，垂直，变化率=0，方向导数为0

参考

[1] 同济大学数学系.高等数学(第六版 下册)[M].高等教育出版社,2007.

[2] 简谈：导数、偏导数、方向导数、梯度向量