计算机图形：法向量变换

目录

• 法向量变换推导
• 法向量变换的应用
  • 何时进行法向量变换
  • Phong明暗处理与法向量变换
• 参考

法向量变换推导

计算机图形：mvp变换（模型、视图、投影变换）描述了对物体的几何图形进行模型、视图、投影变换. 实际应用中，同时需对法向量变换. 切线的变换与图形的几何变换相同，但法向量变换却不同.

法向量变换原则：变换前后，始终与物体表面（切线）垂直.

设物体表面某一点法向量\(\bm{n}\)，切向量\(\bm{t}\). 该点经变换M后得到\(\bm{n'}, \bm{t'}\). 有

\[t'=Mt \]

∵\(\bm{n}⊥\bm{t}\)

∴写成矩阵形式：

\[\tag{1} \begin{aligned} n^Tt&=0\\ \therefore n^TIt&=n^TM^{-1}Mt=(n^TM^{-1})(Mt)=(n^TM^{-1})t'=0 \end{aligned} \]

其中，\(t'\)是所有切向量\(t\)经变换\(M\)得到的向量.

∴\(n^TM^{-1}⊥t_M\)

在3D空间中，能垂直所有变换后的切向量\(t'\)的，只能是一个方向\(n_N^T\)：

\[\tag{2} n_N^T=n^TM^{-1} \]

由(2)

\[\tag{3} n_N=(M)^{-1}n \]

∴\((M)^{-1}\)是\(n\to n_N\)的变换，\(n_N\)是变换后的法向量.

法向量变换的应用

何时进行法向量变换

下图是物体由原始坐标变换到屏幕空间过程示意：

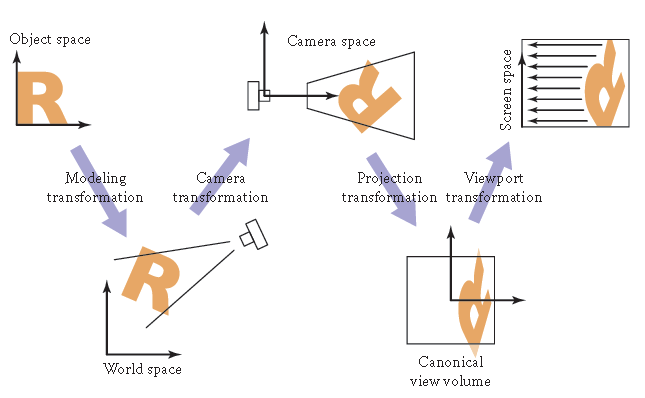
由于法向量主要应用于光照计算，而投影变换会改变法向量大小、方向，所以我们需要在视图空间（/相机空间）中完成光照计算. i.e. 模型变换、相机变换时，需要对法向量进行变换，而投影变换、视口变换则不需要.

Phong明暗处理与法向量变换

Phong明暗处理（见计算机图形：明暗处理）中，我们用双线性插值求法向量，即用三角形顶点的法向量，对三角形内部的点（投影变换、规范化、视口变换后与扫描线相交）的法向量进行线性插值，并没有在屏幕空间利用顶点求法向量，因此不会改变视图空间中得到的法向量方向.

参考

[1] Page127, Shirley P .Fundamentals of Computer Graphics[M]. 2015.

[2] OpenGL Normal Vector Transformation

[3] 图形学基础 - 变换 - 矩阵变换基础

[4] 法向量变换