计算机图形:三维观察之投影变换
投影变换
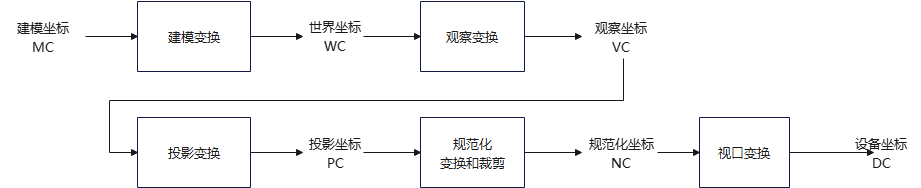
将对象描述从世界坐标系变换到观察坐标系后,要将其投影到观察平面 —— 投影变换。有2种投影方式:
-
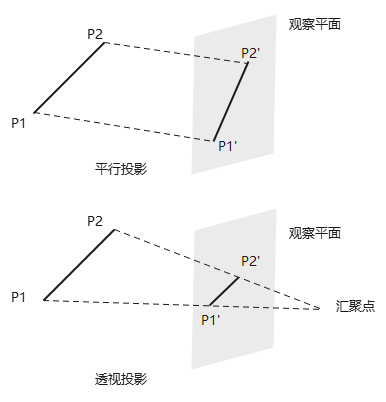
平行投影(parallel projection),坐标位置沿平行线变换到观察平面。保持对象的比例不变,常用于辅助绘图、设计生成工程图。获取对象平行视图的方法有2种:1)正投影:沿垂直于观察平面的直线投影;2)斜投影:沿某倾斜角度投影到观察平面。
-
透视投影(perspective projection),对象位置沿会聚到观察平面后的一点(即投影参考点/投影中心)的直线,变换到投影坐标系。透视投影不会保持对象比例,但真实感更好。
注意:概念上,投影变换指将对象变换到观察平面;实际应用中,投影变换 = 将对象变换到观察平面 + 规范化变换。
线段\(P_1P_2\)的平行投影、透视投影示意:
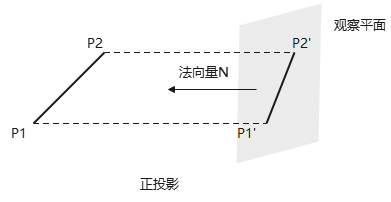
正投影
对象沿与投影平面法向量N平行的方向,到投影平面上的变换N称为正投影(orthogonal projection)或正交投影(orthographic projection)。
正投影:特殊的平行投影,投影线//投影平面法向量N。常用于生成对象的前视图、侧视图、顶视图,可用于建筑和工程绘图。
正交投影分为两步:
1)将点投影到观察平面;
2)规范化变换.
轴测、等轴测正投影
轴测正投影:
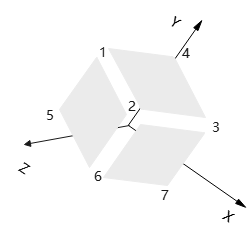
生成显示对象多个侧面的正投影,这些视图称为轴测(axonometric)正投影。
等轴测投影:
等轴测(isometric)投影是特殊轴测投影,其投影平面与每个坐标轴的交点到原点距离相等。
常见等轴测投影:多个投影平面形成一个立方体,立方体8个顶点分布在观察坐标系的8分象限。
正投影坐标系
观察坐标系\(x_{view}y_{view}z_{view}\)下,如果投影方向//\(z_{view}\)轴,则任意点\((x,y,z)\)的投影坐标\((x_p,y_p,z_p)\):
其中,\(z_{vp}\)为观察平面位置(观察平面⊥\(z_{view}\)轴)。\(z_p\)值被保存,用于可见性检测。
任意点到观察平面的正交投影:
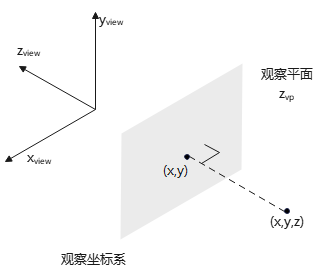
裁剪窗口、正投影观察体
裁剪窗口
常用矩形窗口模拟照相机的镜头,用于确定有多少场景要显示,该矩形称为裁剪窗口。
OpenGL中,裁剪窗口位于观察平面上,位置、大小由矩形左下角+右上角确定,边与观察坐标系\(x_{view}, y_{view}\)轴平行,即\(x_{view}y_{view}\)平面的正则矩形。裁剪窗口边界限定了要显示的场景内容的x、y范围。
观察平面上用观察坐标指定裁剪窗口:
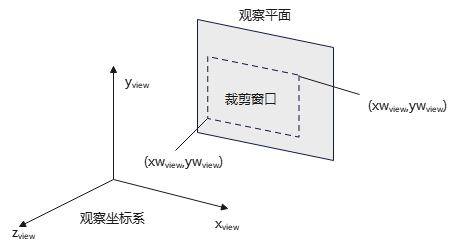
∵正投影的投影线⊥观察平面,裁剪窗口位于观察平面
∴裁剪窗口的4个边界的投影线⊥观察平面
此时,裁剪窗口的4个边界的投影线形成一个无限的裁剪区域,即没有头尾的长方体,如下图:
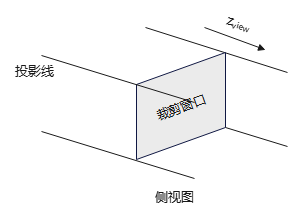
正投影观察体
选择1或2个边界平面(//观察平面),为该(无限裁剪)区域\(z_{view}\)方向限定边界,该区域称为正交观察体(orthographic view volume)或正投影观察体,这2个平面称为近-远裁剪平面(near-far clipping plane)或前-后裁剪平面(front-back clipping plane)。正交观察体外的场景对象会被排除,不会显示。观察方向沿\(-z_{view}\)轴,\(z_{far} < z_{near}\)
由远、近裁剪平面形成的正交投影观察体:
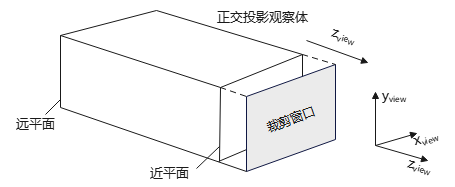
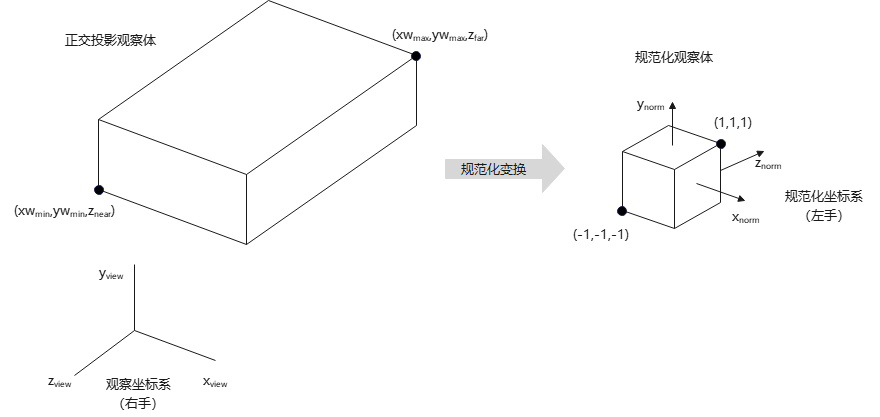
正投影的规范化变换
规范化观察体
观察坐标系下,任一点\((x,y,z)\)到观察平面的正交投影位置\((x,y)(z=n)\)。观察体内的对象,经规范化变换到一个特殊的轴对齐立方体,该立方体称为规范化观察体(normalized view volume/canonical view volume),其内部坐标称为规范化设备坐标(normalized device coordinates,简称NDC)。
规范化观察体有两类:
1)单位立方体:限制x、y、z范围为[0,1];
2)对称立方体:限制x、y、z范围为[-1,1],左手系。
OpenGL,DirectX采用方案
OpenGL采样第2)种规范化观察体.
DirectX与OpenGL不同:将z深度映射到[0,1]而非[-1,1].
为什么规范化观察体用左手系?
屏幕坐标系常用左手系。左手屏幕坐标系:
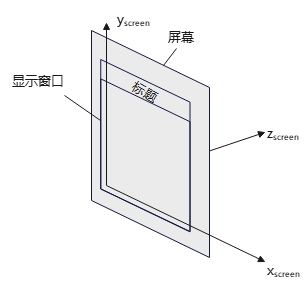
观察方向的正距离有什么含义?
代表视点到屏幕(观察平面)的距离。
规范化变换
设近平面\(z=z_{near}=near=n\)、远平面 \(z=z_{far}=far=f, z_{far}<z_{near}<0\);规范化变换:\((xw_{min},yw_{min},z_{near})\to(-1,-1,-1)\),\((xw_{max},yw_{max},z_{far})\to(1,1,1)\)
因为视线朝着\(-z\)方向,所以要求:\(n=z_{near}>f=z_{far}\).
正交投影的规范化变换示意图:
将变换分解为三步:
1)平移:将观察体中心\((\frac{xw_{min}+xw_{max}}{2},\frac{yw_{min}+yw_{max}}{2},\frac{z_{far}+z_{near}}{2})\)平移到规范化坐标系原点.
平移变换:\(\begin{aligned}
T&=T(-{xw_{min}+xw_{max}\over 2},-{yw_{min}+yw_{max}\over 2},-{z_{near}+z_{far}\over 2})
\end{aligned}\);
2)反射:以z轴为反射轴,将观察体反射,则观察体边界\((z_{near},z_{far})\to (-z_{near},-z_{far})\);
∵\(z_{norm}\)轴与\(z_{view}\)轴反向
∴反射变换(参见计算机图形:特殊几何变换):
3)缩放:将x、y、z坐标从\((xw_{min},xw_{max})、(yw_{min},yw_{max})、(-z_{near},-z_{far})\)放缩到-1~1范围.
放缩变换:
复合变换:
注意:有的文献,z轴变换有差异,因为\(z_{near},z_{far}\)含义不同,或者所采用的NDC不同(左手or右手).
斜投影
当平行投影的投影线与观察平面不平行时,该映射称为斜投影(oblique parallel projection)。
平行投影 = 正交投影 + 斜投影
斜平行投影
如下图,场景中一点\(P(x,y,z)\)在观察平面(\(z_{vp}\))正投影点\(P_1(x,y,z_{vp})\),斜投影点\(P_2(x_p,y_p,z_{vp})\),\(|P_1P_2|=L\)。
斜平行投影用2个角度描述:
1)α,斜平行投影线与\(P_1P_2\)的夹角;
2)φ,\(P_1P_2\)与\(x_{view}\)轴的夹角;
其中,\(α∈[0,π/2),φ∈[0,2π)\)
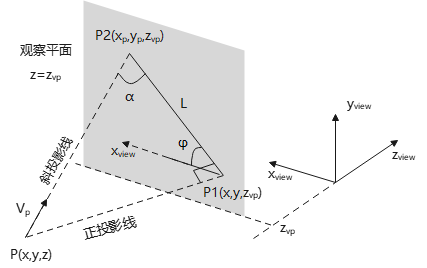
斜投影坐标:
\(\vartriangle PP_1P_2\)中,求L:
当\(z_{vp}-z=1\)时,\(L=\cot α\)
有,
\(α=π/2\)时,可得正投影。
- 斜平行投影向量
斜投影线的方向,称为斜平行向量(parallel-projection vector),用\(V_p\)表示。观察坐标系下,\(V_p=(V_{px},V_{py},V_{pz}), \tan φ={V_{py}\over V_{px}}\),
∵\(V_p//\overrightarrow{P_1P_2}\)
∴\(V_p,\overrightarrow{P_1P_2}\)在\(x_{view},y_{view},z_{view}\)轴分量比例相同(证明见下文),即
于是,斜平行投影可用正交投影向量表示成:
推论:三维空间下,平行向量\(\vec V_1(x_1,y_1,z_1),\vec V_2(x_2,y_2,z_2)\)的xyz坐标分量比例相同,即
\[{x_1\over y_1}={x_2\over y_2},{x_1\over z_1}={x_2\over z_2}, {y_1\over z_1}={y_2\over z_2} \]
证明:
假设\(\vec V_1(x_1,y_1,z_1)//\vec V_2(x_2,y_2,z_2)\),那么,
存在λ∈R且λ≠0,使得
即得证。
斜等测、斜二测平行投影
φ常用π/3(60°)、π/4(45°),显示对象前、侧、顶视图的组合(或前、侧、底)。
α常用值:
1)α=45°(tan α=1),获得视图称为斜等测(cavalier)投影图,垂直于投影平面的线条投影后长度不变。
2)α≈63.4°(tan α=2),获得视图称为斜二测(cabinet)投影图,垂直于投影平面的线条投影后长度为原来一半。真实感较1)更好。
斜平行投影变换
由式(10),可得斜平行投影变换矩阵:
透视投影
将对象沿会聚到投影参考点(projection reference point)或投影中心(center of projection)的路径投影到观察平面来逼近几何光学效果,称为透视投影。
透视投影示意图:
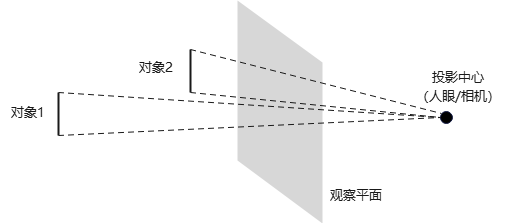
平行投影与透视投影区别
平行投影:保持对象相对比例;
透视投影:模仿人眼或照相机,具有近大远小的真实感。
投影参考点与观察原点
-
投影参考点是透视投影才有的概念;观察原点是基于观察坐标系的概念,所有投影都有。
-
有的图形软件包将投影参考点设在观察原点,即视点;有的将投影参考点作为另一观察参数来选择。i.e. 投影参考点可视作观察原点,也可不同,取决于具体环境,参见下文“特殊透视投影”部分。
坐标变换
场景中任一点\(P(x,y,z)\)到投影参考点\(P_{0}(x_{prp},y_{prp},z_{prp})\)的投影示意图:
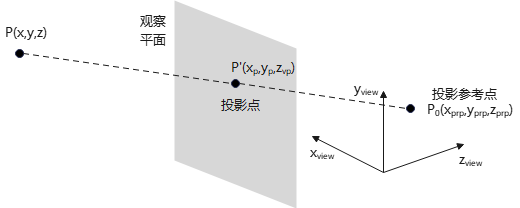
投影线与观察平面交点\(P'(x_p,y_p,z_{vp})\)。
投影线上任一点\((x',y',z')\)参数方程(证明见下面推论):
u=0时,代表点P(x,y,z);
u=1时,代表投影参考点\(P_0(x_{prp},y_{prp},z_{prp})\)。
参数方程写成点形式:
推论(线性插值公式):两点\(S_1(x_1,y_1,z_1)、S_2(x_2,y_2,z_2)\)确定直线段L,L上任一点\(S(x,y,z)\)坐标方程:
\[\begin{cases} x&=ux_1+(1-u)x_2\\ y&=uy_1+(1-u)y_2 & u\in [0,1]\\ z&=uz_1+(1-u)z_2 \end{cases} \]
证明:
∵S位于直线L
∴\(S_1S//S_2S\)
∴存在非0实数λ,使得\(x-x_1=λ(x-x_2)\)
∴\(x={1\over 1-λ}x_1-{λ\over 1-λ}x_2\)
令\(u={1\over 1-λ}\),有\(x=ux_1+(1-u)x_2\)
∵x在线段\(S_1S_2\)上,不妨设\(x_1\le x_2\)
∴\(x_1\le x\le x_2\)
∴\(x_1\le ux_1+(1-u)x_2\le x_2\)
∴\(0\le u\le 1\)
同理可证,y、z坐标也成立。故得证。
证明也可参见:数学基础:三角形重心坐标插值公式的证明
- 如何求投影变换公式?
要求投影变换公式,就需要求出P在观察平面\(z'=z_{vp}\)上的投影点\(P'\)。
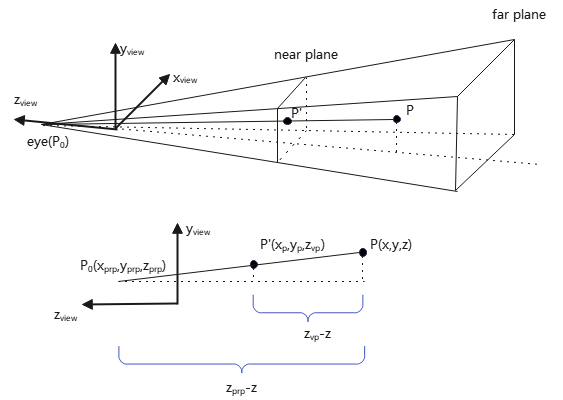
如上图,根据三角形相似性,可求出:
而根据线性插值公式,\(P'(x_p,y_p,z_p)\)坐标:
特殊透视投影
限制投影参考点或观察平面。
1)投影参考点限制在\(z_{view}\)轴,即\(x_{prp}=y_{prp}=0\)
2)将投影参考点固定在原点,即\((x_{prp},y_{prp},z_{prp})=(0,0,0)\)
3)观察平面是uv平面(uvn坐标系),对投影参考点位置不限制,即\(z_{vp}=0\)
tips:uvn坐标系下,\(u,v,n\)分别代表\(x_{view},y_{view},z_{view}\)。参见uvn观察坐标系。
4)观察平面是uv平面,投影参考点在\(z_{view}\)轴,即\(z_{vp}=0,x_{prp}=y_{prp}=0\)
注意:投影参考点不能位于观察平面\(z_{prp}\neq z_{vp}\),否则所有对象投影到观察平面上一点。
灭点
当一个场景使用透视投影到观察平面上时,平行于观察平面的线条投影后仍然平行。但任何与观察平面不平行的平行线组投影后,会成为一组会聚线条。一组投影平行线会聚的点,称为灭点(vanishing point)。每组平行线都有自己的灭点。
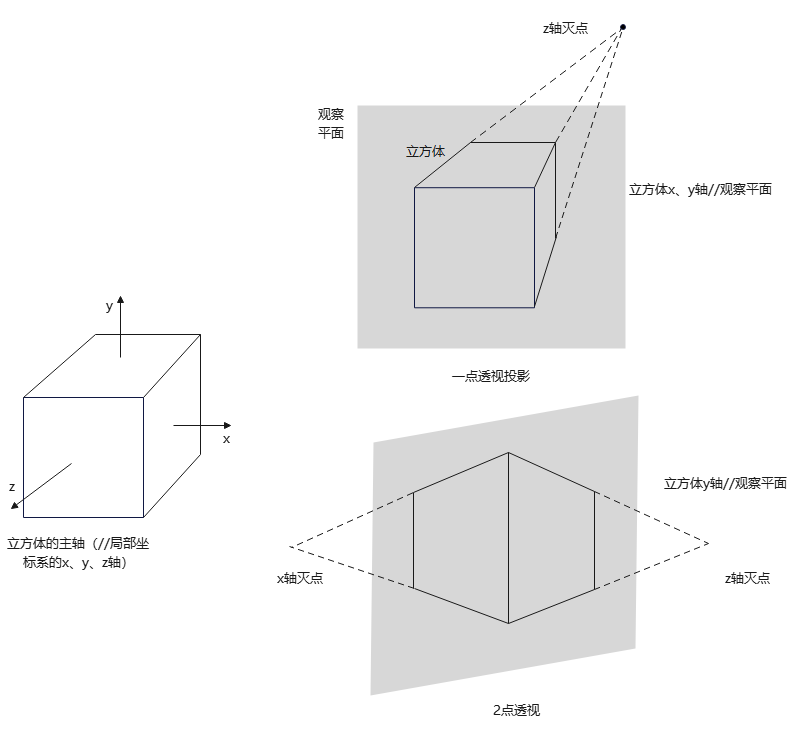
主灭点(principal vanishing point):对象上平行于一个主轴的一组平行线的灭点。坐标轴有3个,所以主灭点最多有3个。
通过投影平面的方向,可以控制主灭点的数量(1,2或3),对应透视投影分为一点、两点或三点投影。
e.g. 立方体的一点、两点透视投影:
灭点与投影参考点
不同点:
- 是否能修改
投影参考点模拟人眼或摄像机,一旦选定,不能随意修改;灭点会随着对象的几何变换而改变位置。
- 针对对象
灭点针对对象的一组平行线,可能有0个或多个;投影参考点针对所有透视投影,只有1个点。i.e. 透视投影一定存在投影参考点,而平行于观察平面的线组不存在灭点。
透视投影观察体
在观察平面上指定一个矩形裁剪窗口,可得到透视投影观察体(perspective projection view volumes),称为视觉棱锥体(pyramid of vision)。棱锥体外的所有对象,都会被裁剪子程序消除。
视觉棱锥体:
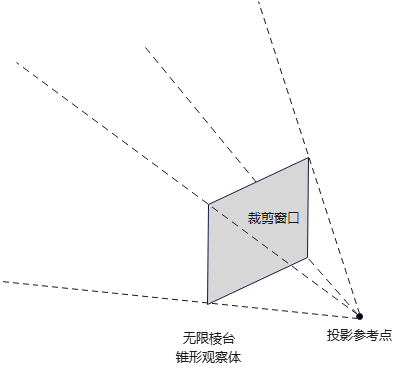
注: 投影中心也是投影参考点。
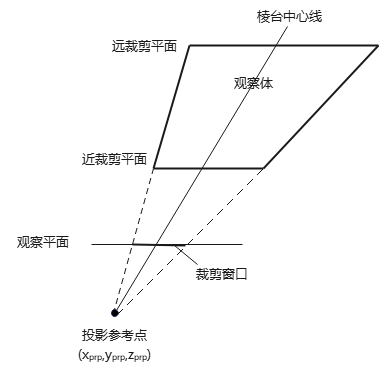
添加垂直于\(z_{view}\)的远、近平面,可得到棱台观察体(frustum view volumes)。通常,远、近平面位于投影参考点同侧(简化版人眼/相机观察模型),且远平面距投影参考点更远。
棱台观察体:
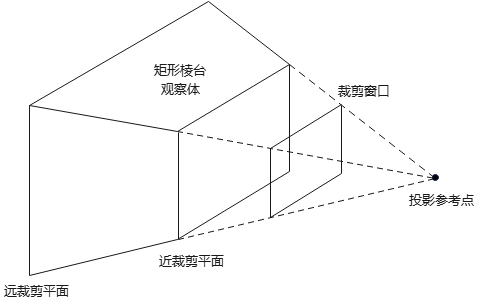
注:有些应用/模型为计算方便,将近裁剪平面设为与观察平面重合.
透视投影变换矩阵
式(14)给出透视投影变换的一般形式,但不能直接得到变换矩阵,因为x、y系数含z(非常数)。可将其转化成别的参数形式,然后再用三维齐次坐标表示:
其中,任一点\(P(x,y,z)\),P的投影点\(P'(x_p,y_p,z_p)\),投影参考点\(P_0(x_{prp},y_{prp},z_{prp})\),观察平面\(z=z_{vp}\)。
齐次参数:
\(x_h,y_h\):
用齐次坐标的矩阵变换表示透视变换:
其中,\(P_h=(x_h,y_h,z_h,h)^T,P=(x,y,z,1)^T\)
可得一种可能的透视投影变换矩阵:
其中,参数\(s_z,t_z\)是z坐标投影值规范化过程中的比例和平移因子,值依赖于棱台观察体范围和规范化范围。如果不放缩、平移,则默认值分别为1, 0。
特例:如果将投影参考点限制在观察原点,且不做规范化和平移即\(s_z=1,t_z=0\),则\((x_{prp},y_{prp},z_{prp})=(0,0,0)\). 那么,\(h=-z\)
对称透视投影椎体
两种描述方法:
1. 使用中心线
从投影参考点到裁剪窗口中心并穿过观察体的线条,是透视投影棱台的中心线。如下图,如果中心线⊥投影平面,则观察体为对称棱台(symmetric frustum)(相对于中心线)。
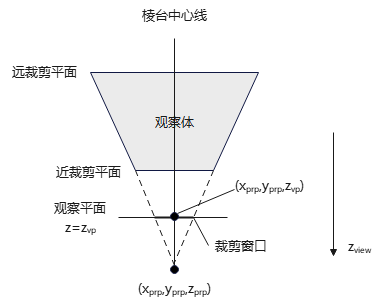
观察坐标系下,观察平面\(z=z_{vp}\),投影参考点\(P_{prp}(x_{prp},y_{prp},z_{prp})\),则中心线与观察平面交于\((x_{prp},y_{prp},z_{vp})\)。裁剪窗口宽、高分别为width、height,则裁剪窗口边界:
注意:\(xw/yw\)中的字母\(w\)指clipping window.
因此,对于对称透视投影锥体,可用裁剪窗口宽、高代替窗口坐标。
2. 使用视场角、裁剪窗口宽高比
视场角(field-of-view angle,简称FOV):棱台的上裁剪平面与下裁剪平面的夹角。对称棱台近似于照相机镜头捕获的场景视锥,可用于度量镜头的尺寸。
注:这里的视场角指垂直视场角(Vertical FOV),由top,bottom平面决定;实际上,还存在水平视场角(Horizontal FOV),有left, right平面决定..
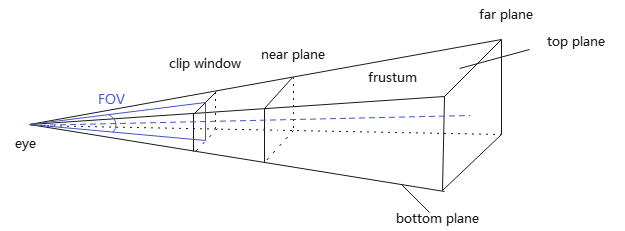
视场角(FOV)与裁剪窗口(clip window)关系:
∴
又裁剪窗口宽高比
对称棱台观察体经透视投影变换后,变成矩形平行管道观察体,变换后的点的范围限制在平行管道观察体内:
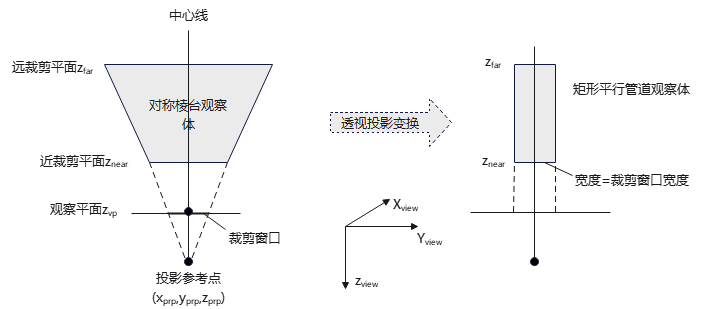
斜透视投影棱台
如果透视投影观察体的中心线不垂直于观察平面,则得到一个斜棱台(oblique frustum)。
斜透视投影 = 错切 + 透视变换
斜棱台顶视图:
斜棱台投影观察体,可通过相对于z轴的x方向、y方向错切(参见三维错切)变换成对称棱台。
为计算方便,将投影参考点设为观察原点,即\((x_{prp},y_{prp},z_{prp})=(0,0,0)\). 可设错切矩阵:
如果观察平面 = 近裁剪平面(即\(z_{vp}=z_{near}\)),则透视投影矩阵可进一步简化。
∵错切将裁剪窗口\((xw_{min},xw_{max},z_{near})\)中心移到观察平面原点\((0,0,z_{near})\)处
∴错切参数\(sh_{zx},sh_{zy}\)满足:
∴有
- 简化(对称)透视投影矩阵
当投影参考点位于观察原点,且近裁剪平面与观察平面重合(OpenGL默认)时,则透视投影变换矩阵(22)可简化为:
其中,z坐标缩放和平移参数\(s_z, t_z\)由规范化确定。\(h=z_{prp}-z=-z\)
- 简化斜透视投影矩阵
将简化后的透视矩阵(27)和错切矩阵(24)合并,可得到将场景中坐标转换为齐次正交坐标系的斜透视投影矩阵。该变换中,投影参考点是观察原点,近裁剪平面是观察平面:
如果裁剪窗口关于观察原点对称,即\(xw_{max}=-xw_{min},yw_{max}=-yw_{min}\),则棱台观察体是对称的,(28)可简化为(27)(无需错切,因为投影参考点位于观察原点)。
透视投影的规范化变换
透视投影最后一步:棱台观察体(矩形平行管道,坐标符合右手系)\(\xrightarrow{规范化}\)规范化观察体(对称立方体,坐标符合左手系)。
透视投影规范化 = 平行管道观察体的正交投影
规范化示意图(近裁剪平面作为观察平面):
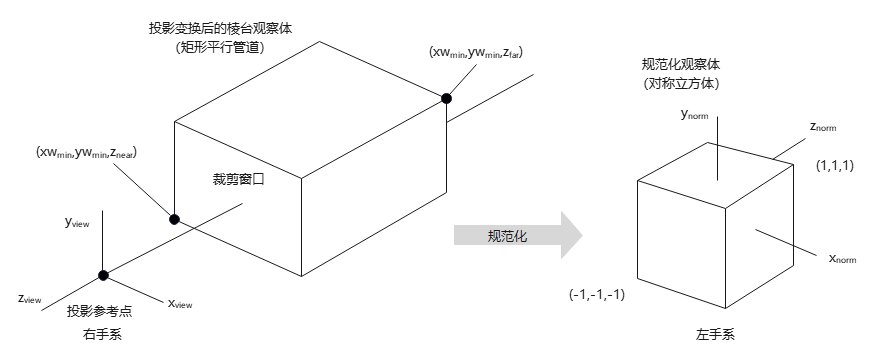
规范化变换中,矩形平行管道中心线\(z_{view}\),在x、y方向不再需要平移,只需要相对于原点的x、y缩放。xy规范化缩放矩阵:
将(28)(29)合并,生成透视投影变换的规范化矩阵:
(30)对应的规范化变换:
∴\(P(x,y,z)\)的投影坐标\(P'(x_p,y_p,z_p)\):
其中,\(h=-z\)
如何确定参数\(s_x,s_y,s_z,t_z\)?
坐标映射:\((xw_{min},yw_{min},z_{near})\xrightarrow{}(-1,-1,-1), (xw_{max},yw_{max},z_{far})\xrightarrow{}(1,1,1)\).
\(s_x,s_y\)分别将长度\(xw_{max}-xw_{min},yw_{max}-yw_{min}\)放缩为新长度2,2
∴
\(s_z,t_z\)将输入坐标\(z_{near},z_{far}\)分别转换为\(-1,1\)
∴需满足
∴有
∴代入(30)可得
这就是透视投影(包括规范化)矩阵.
注意:该投影矩阵对应模型与OpenGL约定一致,包括
1)观察坐标系为右手系统,规范化坐标系为左手系统;
2)投影参考点位于观察原点,观察平面位于近裁剪平面;
3)远、近裁剪平面关系:\(z_{far}<z_{near}<0\)(包含符号).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号