计算机图形：全局光照

目录

什么是全局光照

前面计算机图形：光照模型讲的是局部光照，通过对象表面和光源的入射光线实现表面绘制.

但真实的光照效果，还包括从其他对象反射的光线，也会产生明暗效果. 这种光照计算的模型，称为全局光照.

光线追踪方法

光线追踪（ray tracing，光线追踪）是一种全局光照方法，核心思想：沿着到达视点的光线的反方向，从视点出发经过图像平面每个像素，找出与视线相交的物体表面点\(P_0\)，继续跟踪，找出影响\(P_0\)点光强的所有光源，从而算出\(P_0\)点精确的光强.

优缺点：
能生成高度真实感图形，但对于表面光滑的对象，需要惊人的计算量.

img

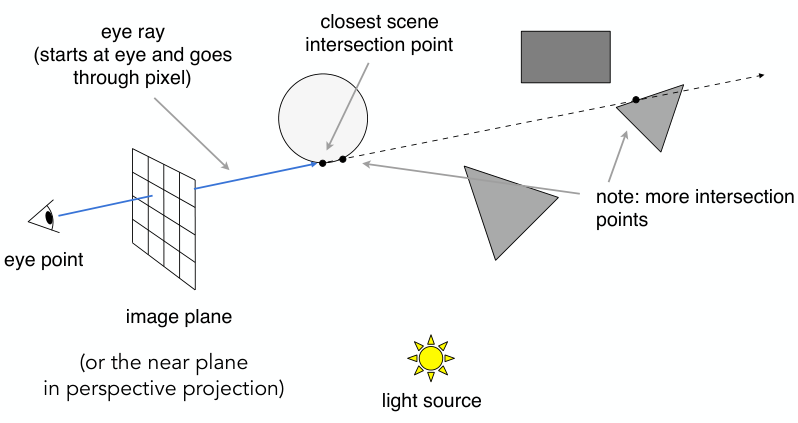
基本光线追踪算法

步骤：

  1. 建立参考坐标系
    投影参考点（视点）在z轴、像素位置在xy平面.

  2. 生成像素光线
    在该坐标系统中，描述场景的几何数据、生成像素光线.
    像素光线从投影参考点出发，穿过每个像素中心进入场景，并沿反射和透射（折射）路径形成各种光线分支.

  3. 计算光强贡献
    在表面交点（光线入射点）计算像素强度的贡献.

  4. 相交测试
    生成像素光线后，需测试场景中所有对象表面是否与之相交. 如果相交，则计算出交点到像素的距离.
    计算出所有表面与该光线的交点后，距离最小的交点，即代表该像素所对应的可见面.

  5. 确定反射、折射路径
    将该光线在该可见面上沿镜面反射路径（反射角=入射角）反射. 如果表面是透明的，还需考察折射光线.
    反射、折射光线，统称从属光线（secondary ray）.

  6. 递归处理从属光线
    对每条从属光线重复该光线处理过程. 如果有表面和其相交测试确定最近的相交表面，则递归地在沿从属光线方向最近的对象表面上生成下一条折射和反射光线.
    像素（发出的）光线在场景中被反射、折射时，逐个将相交表面加入到一个二叉光线追踪树（ray-tracing tree）. 树的做枝表示反射光线，右枝表示透射光线（折射）. 光线追踪的最大深度可由用户指定，或由存储容量决定.

  7. 递归结束
    当满足下列任一条件，就停止跟踪：
    (1) 该光线不与任何表面相交
    (2) 该光线与一个光源相交且该光源不是一个反射面
    (3) 该树到达最大允许深度

步骤3如何计算光强贡献？
在每一表面交点，引入基本光照模型确定表面强度的贡献. 强度值存放在像素树（光线追踪树？）的表面节点位置. 与非反射面光源（点光源？）相交的光线，可用该光源对强度赋值.

求从属反射、透射光线方向

  • 镜面反射

如下图所示，入射光线u由视点发出，射向物体表面得到反射光线R，物体表面单位法向量N，射向点光源的单位向量L，入射角为α，反射角β.

img

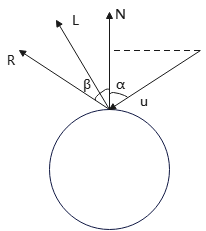
有
\((-\bm{u})\cdot \bm{N} = |-\bm{u}| |\bm{N}|\cos α=|-\bm{u}|\cos α\)

-u在N方向投影：\(-\bm{u_1}=(|-\bm{u}|\cos α)\bm{N}=((-\bm{u})\cdot \bm{N})\bm{N}=-(\bm{u}\cdot \bm{N})\bm{N}\)

由反射定律知，β=α，即N是R、-u的半角向量，有

\[\begin{aligned} &\bm{R}+(-\bm{u})=2(-\bm{u_1})\\ \implies &\bm{R}=\bm{u}-2(\bm{u}\cdot \bm{N})\bm{N} \end{aligned} \]

  • 折射（透明表面）

如下图，入射光线u由视点发出，折射光线T，物体表面单位法向量N，入射角\(θ_i\)，折射角\(θ_r\).

img

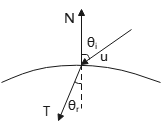
计算机图形：光照模型中有关折射率的部分，已经证明T可以用N、u表示：

\[\bm{T}=\frac{θ_i}{θ_r}\bm{u}-(\cos θ_r - \frac{\eta_i}{\eta_r}\cos θ_i)\bm{N} \]

其中，\(\eta_i\)和\(\eta_r\)分别表示入射材料和折射材料的折射率.
而折射角\(θ_r\)可由折射定律（Snell定律）得到：

\[\begin{aligned} &∵\eta_i\sin θ_i=\eta_r\sin θ_r\\ &∴\cos^2 θ_r=1-\sin^2 θ_r=1-(\frac{\eta_i}{\eta_r})^2\sin^2 θ_i=1-(\frac{\eta_i}{\eta_r})^2(1-\cos^2 θ_i)\\ &∵θ_r\in [0, \pi]\\ &∴\cos θ_r=\sqrt{1-(\frac{\eta_i}{\eta_r})^2(1-\cos^2 θ_i)} \end{aligned} \]

如何确定像素光线是否与对象表面相交？
这是接下来的内容.

光线与对象表面的求交

  • 光线方程

光线由起始点\(\bm{P_0}\)和方向向量\(\bm{u}\)表示. 对应光线方程（ray equation）：

\[\bm{P}: \bm{r}(s)=\bm{P_0}+s\bm{u}, 0\le s < ∞ \]

其中，\(\bm{P_0}\)是初始位置，初值可设为观察平面某个像素点\(\bm{P_{pix}}\)或投影参考点（即视点）. s是沿着\(\bm{u}\)方向到\(\bm{P_0}\)的距离，负值无意义. 初始\(\bm{u}\)可由投影参考点\(\bm{P_{prp}}\)和光线穿过的像素位置\(\bm{P_{pix}}\)得到：

\[\bm{u}=\frac{\bm{P_{pix}-\bm{P_{prp}}}}{|\bm{P_{pix}-\bm{P_{prp}}}|} \]

单位化\(\bm{u}\)能节省后续计算量.

光线方程写成向量形式：

\[\overrightarrow{P_0P}=s\bm{u}, 0\le s < ∞ \]

只需求出s，就能得到光线与对象表面交点\(\bm{P}\).

光线每次与表面相交，\(\bm{P_0},\bm{u}\)由交点处的从属光线更新，进而求出下一次迭代的从属光线：反射光线\(\bm{R}\)，折射光线\(\bm{T}\).

  • 求交点

光线方程，将光线与对象的求交，转化为求\(\bm{P_0}\)沿\(\bm{u}\)方向到对象表面距离s. 于是，可联立光线方程和描述表面的方程，求解s.

光线-平面求交

img

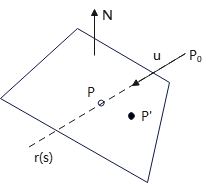
图中，\(\bm{P}\)是平面上任意一点，\(\bm{P'}\)是平面上一固定点，\(\bm{N}\)是平面法向量.

光线方程：

\[r(s)=\bm{P_0}+s\bm{u},0\le s < ∞ \]

平面方程（点法式）：

\[\bm{P}: (\bm{P}-\bm{P'})\cdot \bm{N}=0 \]

联立上面2个方程求交点，可得

\[\begin{aligned} &(\bm{P_0}+s\bm{u}-\bm{P'})\cdot \bm{N}=0\\ &s=\frac{(\bm{P'}-\bm{P_0})\cdot \bm{N}}{\bm{u}\cdot \bm{N}}, 0\le s<∞ \end{aligned} \]

光线-三角形求交：Möller-Trumbore算法

算法能快速求出光线与三角形的交点，而无需计算平面方程. 将光线\(\bm{r}(s)=\bm{P_0}+s\bm{u}\)与\(△A_0A_1A_2\)的交点，用重心坐标表示：

\[\tag{1} \bm{P_0}+s\bm{u}=α\bm{A_0}+β\bm{A_1}+γ\bm{A_2}, 0\le s, α+β+γ=1 \]

可解得：

\[\begin{aligned} \begin{bmatrix} s\\β\\γ \end{bmatrix}= \frac{1}{\bm{S_1\cdot \bm{e_1}}}\begin{bmatrix} \bm{S_2\cdot \bm{e_2}}\\ \bm{S_1\cdot \bm{S}}\\ \bm{S_2\cdot \bm{u}} \end{bmatrix},\\ \bm{e_1}=\bm{A_1}-\bm{A_0}, \bm{e_2}=\bm{A_2}-\bm{A_0},\\ \bm{S}=\bm{P_0}-\bm{A_0},\bm{S_1}=\bm{u}\times \bm{e_2},\bm{S_2}=\bm{S}\times \bm{e_1} \end{aligned} \]

证明：

\[\begin{aligned} &∵\bm{P_0}+s\bm{u}=α\bm{A_0}+β\bm{A_1}+γ\bm{A_2},α+β+γ=1\\ &∴\bm{P_0}+s\bm{u}=(1-β-γ)\bm{A_0}+β\bm{A_1}+γ\bm{A_2}\\ &∴\bm{P_0}-\bm{A_0}=β(\bm{A_1}-\bm{A_0})+γ(\bm{A_2}-\bm{A_0})-s\bm{u}\\ \end{aligned} \]

方程组写成矩阵形式：

\[\tag{2} \begin{bmatrix} -\bm{u}&\bm{e_1}&\bm{e_2} \end{bmatrix} \begin{bmatrix} s\\β\\γ \end{bmatrix}=\bm{S},\\\bm{e_1}=\bm{A_1}-\bm{A_0},\bm{e_2}=\bm{A_2}-\bm{A_0},\bm{S}=\bm{P_0}-\bm{A_0} \]

形如方程组\(Ax=b\). 由Cramer 法则（见高等代数笔记：克莱姆法则（Cramer's Rule））知，当\(|A|\neq 0\)时，方程组有唯一解：\((x_1,x_2,...,x_n)\). 其中，

\[x_j=\frac{|B_j|}{|A|},j=1,2,...,n \]

显然，\(\bm{e_1,e_2}\)位于三角形所在平面，而\(-\bm{u}\)是光线的反向
∴三者不同面（通常忽略共面的情况），即\(\begin{vmatrix}-\bm{u}&\bm{e_1}&\bm{e_2}\end{vmatrix}\neq 0\)
∴方程组(2)有唯一解\((s,β,γ)\).

\[s=\frac{|B_1|}{|A|}=\frac{\begin{vmatrix}\bm{S}&\bm{e_1}&\bm{e_2}\end{vmatrix}}{\begin{vmatrix}-\bm{u}&\bm{e_1}&\bm{e_2}\end{vmatrix}} \]

由混合积的坐标计算（见解析几何笔记：向量的外积定理3及常用性质）知，

\[\begin{aligned} s&=\frac{\begin{vmatrix}\bm{S}&\bm{e_1}&\bm{e_2}\end{vmatrix}}{\begin{vmatrix}-\bm{u}&\bm{e_1}&\bm{e_2}\end{vmatrix}}=\frac{\bm{S}\times \bm{e_1}\cdot \bm{e_2}}{\bm{-u}\times \bm{e_1}\cdot \bm{e_2}}\\ &=\frac{\bm{S}\times \bm{e_1}\cdot \bm{e_2}}{\bm{e_1}\times \bm{u}\cdot \bm{e_2}}=\frac{\bm{S}\times \bm{e_1}\cdot \bm{e_2}}{\bm{e_1}\cdot (\bm{u}\times \bm{e_2})}\\ &=\frac{\bm{S_2}\cdot \bm{e_2}}{\bm{e_1}\cdot \bm{S_1}}=\frac{\bm{S_2}\cdot \bm{e_2}}{\bm{S_1}\cdot \bm{e_1}} \end{aligned} \]

同理，

\[\begin{aligned} β&=\frac{|B_2|}{|A|}=\frac{\begin{vmatrix}\bm{-u}&\bm{S}&\bm{e_2}\end{vmatrix}}{\begin{vmatrix}-\bm{u}&\bm{e_1}&\bm{e_2}\end{vmatrix}}=\frac{\bm{-u}\times \bm{S}\cdot \bm{e_2}}{\bm{S_1}\cdot \bm{e_1}}\\ &=\frac{\bm{S}\times \bm{u}\cdot \bm{e_2}}{\bm{S_1}\cdot \bm{e_1}}=\frac{\bm{S}\cdot (\bm{u}\times \bm{e_2})}{\bm{S_1}\cdot \bm{e_1}}\\ &=\frac{\bm{S}\cdot \bm{S_1}}{\bm{S_1}\cdot \bm{e_1}}=\frac{\bm{S_1}\cdot \bm{S}}{\bm{S_1}\cdot \bm{e_1}}\\ γ&=\frac{|B_3|}{|A|}=\frac{\begin{vmatrix}\bm{-u}&\bm{e_1}&\bm{S}\end{vmatrix}}{\bm{S_1}\cdot \bm{e_1}}=\frac{\bm{-u}\times \bm{e_1}\cdot \bm{S}}{\bm{S_1}\cdot \bm{e_1}}\\ &=\frac{\bm{S}\cdot (\bm{e_1}\times \bm{u})}{\bm{S_1}\cdot \bm{e_1}}=\frac{\bm{S}\times \bm{e_1}\cdot \bm{u}}{\bm{S_1}\cdot \bm{e_1}} \end{aligned} \]

光线-球面求交

球体：光线追踪中最简单的对象.
给定半径r、中心\(P_c\)的球体，球面任意点P满足球面方程：

\[|\bm{P}-\bm{P_c}|^2-r^2=0 \]

img

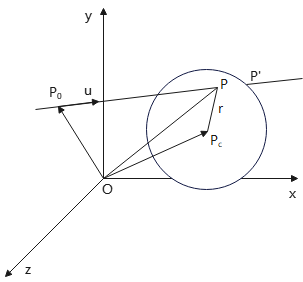
∵交点P在光线u上
∴P满足光线方程：

\[\bm{P}=\bm{P_0}+s\bm{u} \]

代入球面方程：

\[|\bm{P_0}+s\bm{u}-\bm{P_c}|^2-r^2=0 \]

令\(Δ\bm{P}=\bm{P_c}-\bm{P_0}\)，而\(|\bm{u}|=1\)，可得：

\[\begin{aligned} |Δ\bm{P}+s\bm{u}|^2-r^2&=0\\ s^2(|\bm{u}|^2)+2(Δ\bm{P}\cdot \bm{u})s+|Δ\bm{P}|^2-r^2&=0\\ s^2+2(Δ\bm{P}\cdot \bm{u})s+|Δ\bm{P}|^2-r^2&=0 \end{aligned} \]

利用一元二次方程（\(ax^2+bx+c=0\)）求根公式（\(x=\frac{b±\sqrt{b^2-4ac}}{-2a}\)），可解得：

\[s=\bm{u}\cdot Δ\bm{P}±\sqrt{(\bm{u}\cdot Δ\bm{P})^2-|Δ\bm{P}|^2+r^2} \]

以下两种情况，不再考虑该球面：
1）如果无（实数）解，即\(\sqrt{Δ}\)无意义，说明光线与球面不相交；
2）如果2个根均为负，说明球面在\(\bm{P_0}\)之后，即沿着\(\bm{u}\)反向.

如果2个根均为正，则取s为模更小的那个.

  • 优化

对于远离光束出发点的小球体，即\(r^2\ll|Δ\bm{P}|^2\)，求根近似运算时容易丢失\(r^2\)项.

此时，可重新计算s以消除误差：

\[s=\bm{u}\cdot Δ\bm{P}±\sqrt{r^2-|Δ\bm{P}-(\bm{u}\cdot Δ\bm{P})\bm{u}|^2} \]

证明：

\[\begin{aligned} Δ&=r^2-|Δ\bm{P}-(\bm{u}\cdot Δ\bm{P})\bm{u}|^2\\ \Leftrightarrow Δ&=r^2-|Δ\bm{P}|^2-(\bm{u}\cdot Δ\bm{P})^2+2(Δ\bm{P}(\bm{u}\cdotΔ\bm{P})\bm{u})\\ \Leftrightarrow Δ&=r^2-|Δ\bm{P}|^2+(\bm{u}\cdot Δ\bm{P})^2 \end{aligned} \]

即得证.

光线-多面体求交

多面体更复杂. 光线与多面体一般求交过程：

1）包围体求交

先用光线与包围体（如球、长方体等）进行求交测试，以提高效率. 如一个被球体包围的多面体，如果光线与球面无交点，则无需再对多面体进行测试.

2）剔除后表面

测试不等式：

\[\bm{u}\cdot \bm{N} < 0 \]

其中，u是光线方向，N是表面法向量.

如果该不等式，说明该面为前表面；否则，为后表面. 后表面需要剔除，无需进一步考虑.

3）联立方程求交点

如何求光线与前表面交点P？

思路：联立多面体表面方程与光线方程，得到参数s.

设前表面所在平面方程：
\(Ax+By+Cz+D=0\)

则法向量\(N=(A,B,C)\)，参数\(A,B,C,D\)可由前表面3个顶点确定（不共线三点确定一个平面）.

前表面任一点\(P(x_p,y_p,z_p)\)满足平面方程：

\[\bm{N}\cdot \bm{P}=(A,B,C)\cdot (x_p,y_p,z_p)=Ax_p+By_p+Cz_p=-D \]

将光束方程\(\bm{P}=\bm{P_0}+s\bm{u}\)代入上式：

\[\bm{N}\cdot(\bm{P_0}+s\bm{u})=-D \]

可得，

\[s=-\frac{D+\bm{N}\cdot \bm{P_0}}{\bm{N}\cdot \bm{u}} \]

其中，s代表光线初始位置\(P_0\)沿着光束方向\(\bm{u}\)到达多边形一个表面所在平面的距离.

4）光线与多边形相交测试（内-外测试）

多边形是一个有限区域（并非无限平面），因此还需确定光线是否与该表面相交，可对通过1）的表面进行内-外测试.
前面计算机图形：输出图元讲过，这里复习下. 内外测试法用于判断对象的内部区域，有2种常用方法：奇偶规则、非零环绕数规则.

奇偶规则：从任意位置P到对象坐标范围以外的远点画一条概念上的射线，统计该射线与各边的交点数目. 如果交点数目为奇数，则P是内部点；否则P是外部点.

非零环绕数规则：统计多边形以逆时针方向环绕某一特定点的次数，称为环绕数，初值0. 从任意位置P到对象坐标范围外的远点画一条射线，射线不能与多边形顶点相交. 当P沿着射线方向移动时，统计穿过该射线的边的方向. 当多边形从右到左穿过射线时，环绕数+1；从左到右时，环绕数-1. 所有穿过的边都已经计数后，环绕数最终值决定了P的相对位置：如果环绕数≠0，则P定义为内部点；否则，P是外部点.

减少求交计算/加速求交

光线追踪中，约95%时间用于光线与表面求交. 求交计算中，大部分时间用于计算沿光束方向不可见对象的求交.

如何减少求交计算时间？
3类方法：包围盒，空间划分（Spatial partitions），物体划分（Object partitions）.

包围盒

包围盒：将相邻对象用一个包围盒（盒或球）包起来. 如果光线未与包围盒相交，则肯定不与对象相交.

img

最常用的包围盒，是由3组平行对板构成的轴对齐包围盒（Axis-Aligned Bounding Box, 简称AABB），任意一侧平行于x,y或z轴.

img

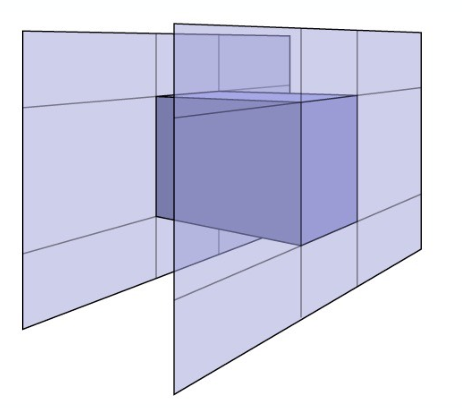
如何判断光线与AABB盒相交？

如下图，对于2D（3D类似）：

img
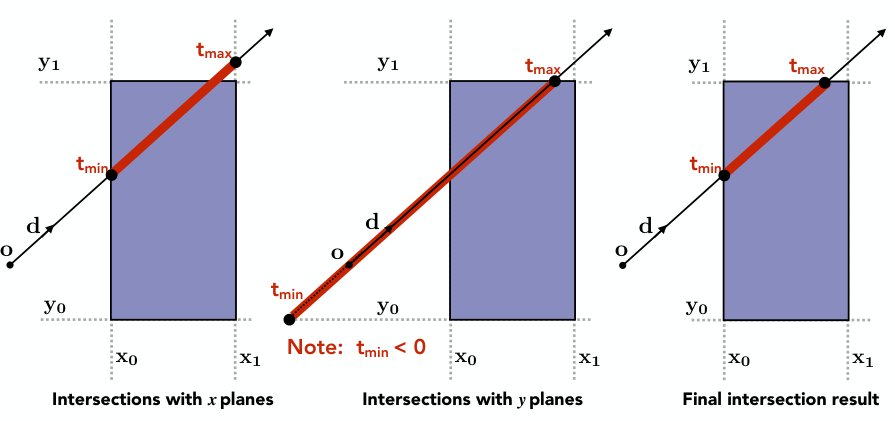
注：图中t与光线方程参数s含义相同.

射线与\(x_0x_1\)对板相交的线段，射线与\(y_0y_1\)对板相交的线段，这2个线段求交集得到射线与2D包围盒相交的线段.

i.e. 相交部分线段参数t满足：

\[t_{enter}=max\{t_{min}\},t_{exit}=min\{t_{max}\}, t_{enter} < t_{exit}\space and\space t_{exit}>=0 \]

为什么选用轴对齐包围盒（AABB），而不直接求光线与平面交点？

因为能极大减少计算量.
光线与平面求交：

img

\[s=\frac{(\bm{P'}-\bm{P_0})\cdot \bm{N}}{\bm{u\cdot N}} \]

每个x、y、z坐标都进行3次减法、2次乘法（内积），最后1次乘法.

光线与AABB包围盒的某一对板（轴对齐）求交：
以垂直于x轴对板为例，法向量为x轴，即\((1,0,0)\)，那么

\[s=\frac{p'_x-p_{0x}}{u_x} \]

1次减法，1次除法.

均匀网格(Uniform Grids)

思想：将空间（场景的AABB盒）划分为多个均匀的网格单元（cells），光线先与网格求交，如果光线与网格相交，再对光线与网格内物体求交；如果光线与网格不相交，那么光线肯定不与其内物体相交.

2D均匀网格

对于2D情形，如下图，
先构建均匀网格，将物体存放在单元格中（一个cell可能存放多个物体，一个物体可能位于多个cell中）：

img

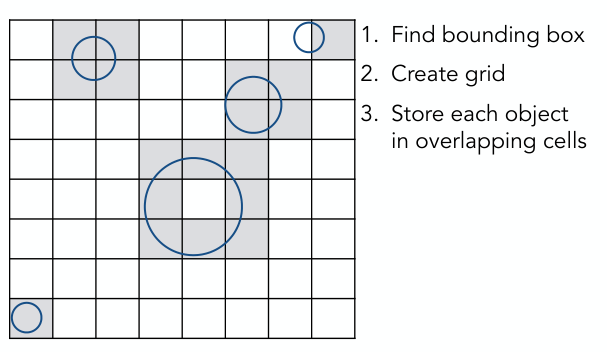
沿着光线方向，对与光线相交的每个网格cell，遍历包含在其中的所有物体，并与光线求交：

img

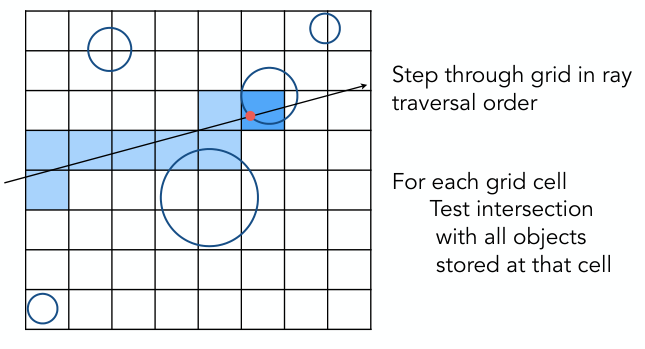
如何快速知道哪些cell与光线相交？

类似于Bresenham算法，从光线的起始cell开始，当光线斜率>=0时，下一个相交cell只可能是右边或右上的；当斜率<0时，下一个相交cell只可能是右边或右下的.

img

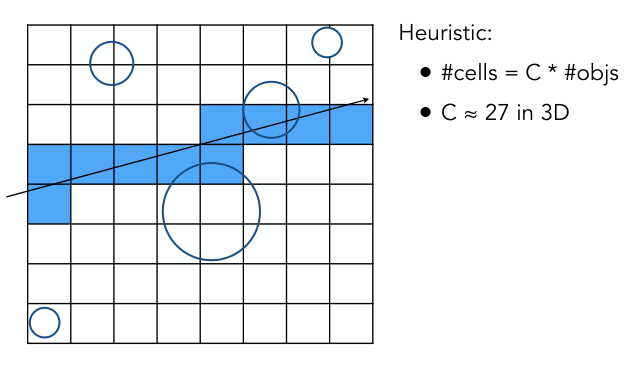
网格分辨率多少合适？

如果只有一个cell，那么起不到加速效果；
如果cell太多，遍历无关的cell反而导致效率降低；
经验值：cell数量 = C * 对象数量，常数C约为27.

3D均匀网格

将场景包围盒划分为若干个等大小的子立方体，然后将子立方体继续划分，直到每个子立方单元所包含的物体数量 ，称为体元（Voxel）.

img

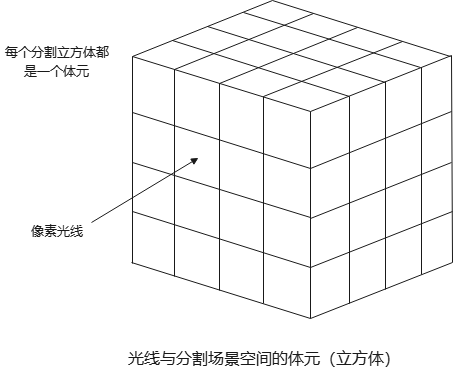
空间划分(Spatial Partitions)

空间划分：将整个场景包含在一个立方体中，然后将立方体逐次分割，直到每个子立方体（体元，Voxel）单元所包含的对象的表面或表面数目 ≤ 预设最大值.

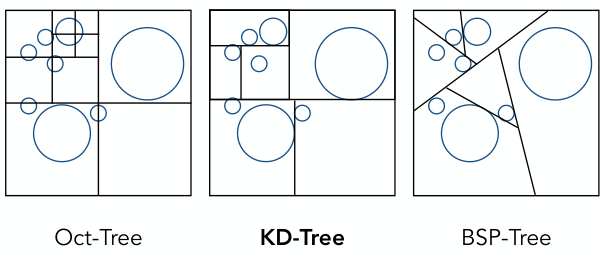
有3种常用算法：八叉树（Oct-Tree）、KD树（KD-Tree）、BSP树（BSP-Tree）. 都适用于2D、3D场景.

  • 八叉树：直接用一横、一竖将空间对半切. 在2D场景下，其实是4叉树（4个子块）；在3D场景下，才是八叉树（8个子块）；在线段情况下，其实是二叉树（2个子块）.

切到什么时候为止？
4个子块中，其他3个子块都与任何物体都不相交. 因此，复杂度为\(2^n\).

  • KD-Tree与Oct-Tree几乎完全相同，区别：KD-Tree每次总是沿着平行某个轴的方向，将空间切开. 有一种切分策略是取块内排号为中位数的物体，以使两侧子块内物体数量大致相等.

先水平切，再竖直切. 如此循环往复，能确保空间是大致均匀的划分.

  • BSP-Tree：对空间进行二分. 每次选一个方向，将所在空间分为2部分. 与KD-Tree区别在于：不是沿着某一个轴切的

img

KD树

KD树的构建：

1）初始时，用竖直线划分包围盒A，得到2个子块

img

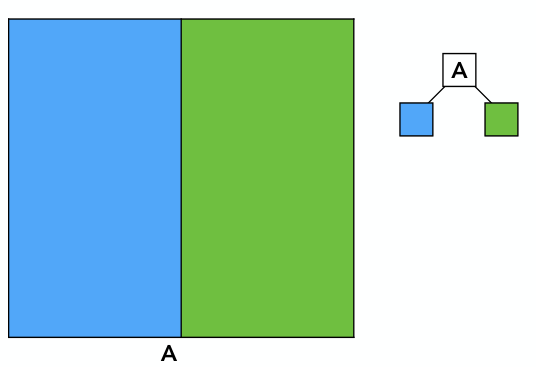
2）接着，继续对右孩子用水平线划分

img

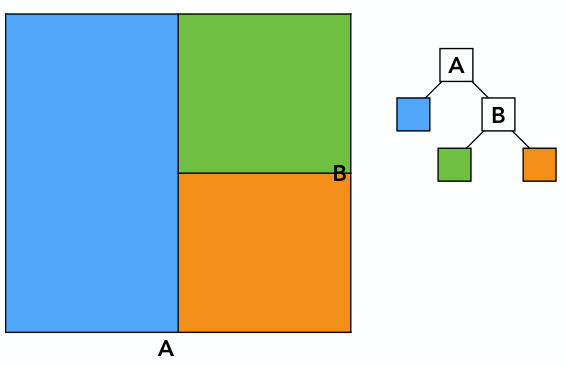
3）如此循环往复，最终得到如下图的划分，每个划分对应一种树形数据结构：

img

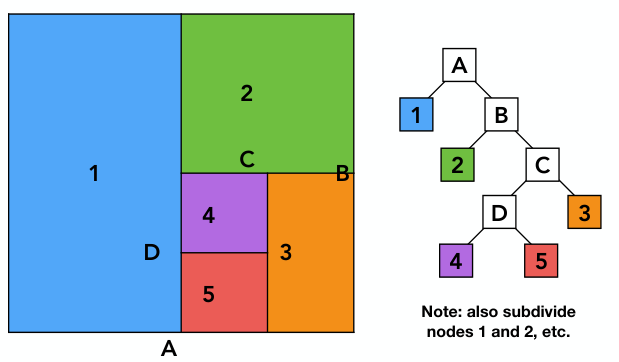
内部节点（非叶子节点）存储：

  • 划分轴：x/y/z轴
  • 划分位置：划分平面的位置
  • 孩子：指向所有孩子节点的指针
  • 不存储任何物体

叶子节点存储：

  • 物体列表

遍历KD树并求交：

某一束光线与KD树的相交情况如下，如何遍历KD树，并用它加速与物体求交？
思想：从根节点开始遍历KD树，光线与当前节点对应包围盒求交. 相交时，如果是内部节点，则需迭代光线与子节点求交；如果是叶子节点，则将光线与所包含所有物体求交. 不相交时，直接忽略.

光线与节点求交，是指求出光线与对应包围盒的入口点、出口点，分别记为\(t_{min}, t_{max}\)；光线与物体求交，则是前面提到的光线-对象表面的求交.

img

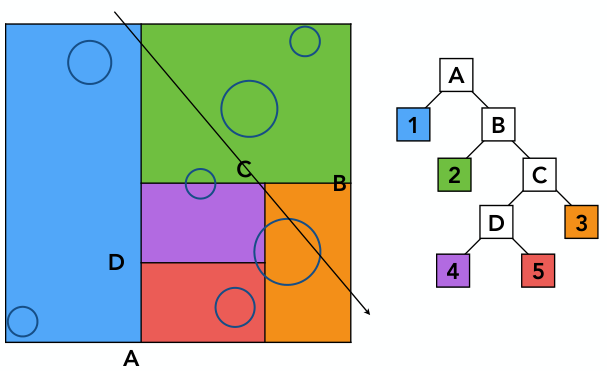
详细步骤：

1）光线与根节点A求交

img

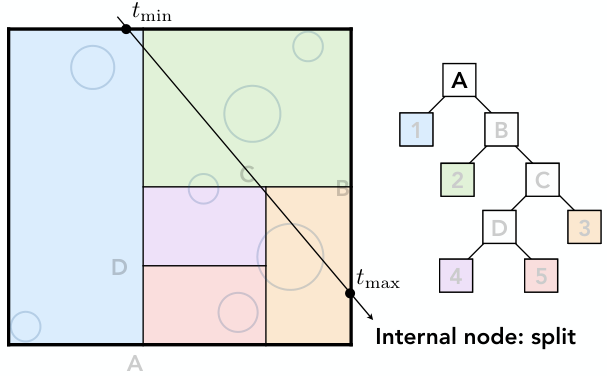
2）光线与A的左右孩子求交

左孩子1是叶节点，右孩子B是内部节点. 因此，光线与节点1内所有物体求交，与B孩子迭代求交

img

img

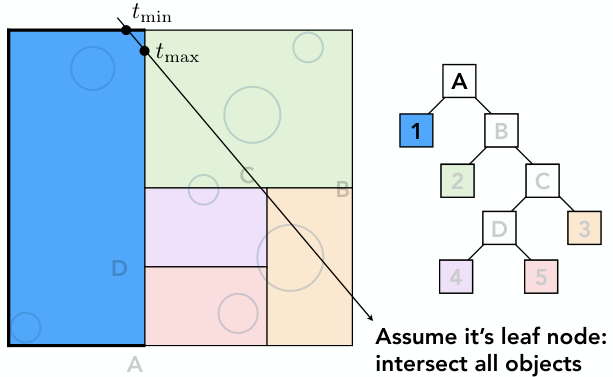
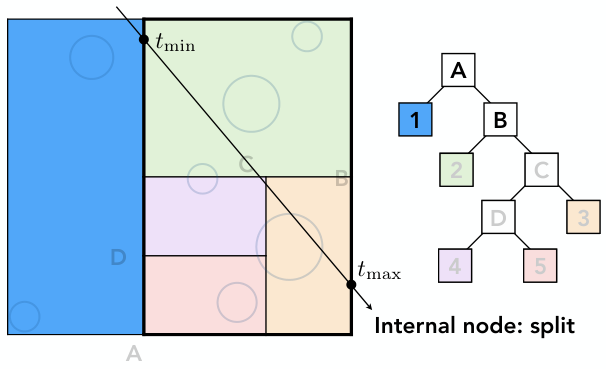
3）光线与B的左右孩子求交

左孩子2是叶节点，右孩子C是内部节点. 因此，光线与节点2内所有物体求交，与C孩子迭代求交

img

img

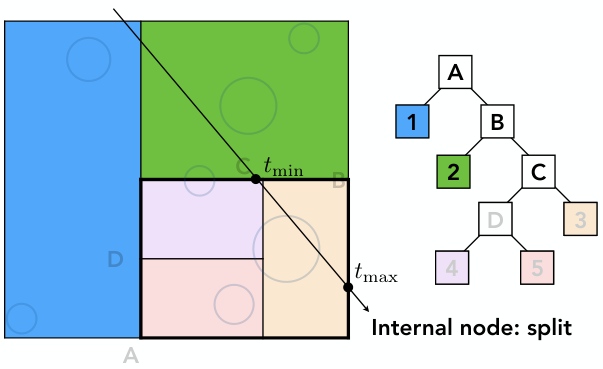
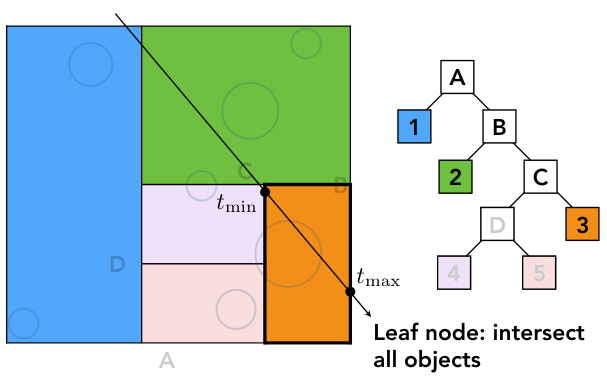
4）如此循环往复，直到遍历完所有树节点，进而求出光线与物体的所有交点.

物体划分(Object Partitions)

层次包围盒（BVH）

八叉树、KD树、BSP树都是按空间划分，一个物体可能存在多个子包围盒中，而造成光线与物体多次求交；盒子太小，也可能位于三角形内，从而难以求交.

于是，提出另一种基于分割算法 —— 层次包围盒（Bounding Volume Hierarchy, BVH），一个物体只存在于一个子包围盒中.

构建BVH步骤：

1）找到一个包围盒；
2）通过将包围盒内物体拆成2个部分，从而递归的将包围盒分成2个；
3）2个部分重新计算包围盒；
4）当子包围盒内物体/三角形数足够少时（例如设置阈值5），停止递归；
5）将物体存放到叶子节点中.

img

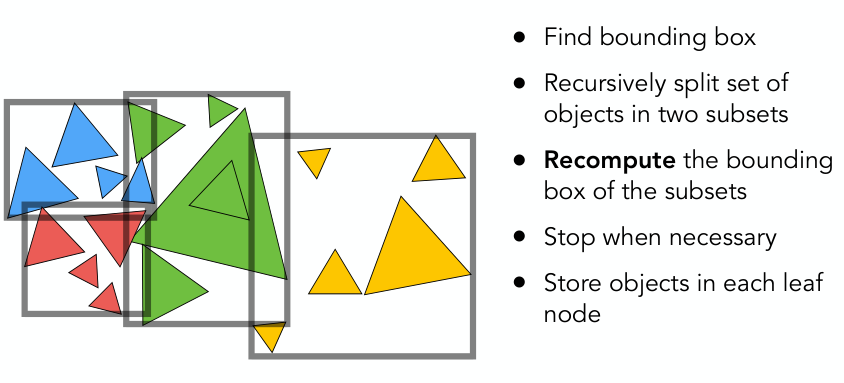
而怎么划分节点，当前有很多研究. 几个常见做法：
1）沿着最长的轴，将物体分为2部分，两边物体/三角形数尽量相等；
2）取中间物体（中位数）进行划分（偶数取较大中位数）；

内部节点存储：

  • 包围盒
  • 子节点：指向孩子节点的指针

叶子节点存储：

  • 包围盒
  • 物体列表

BVH遍历并求交伪代码：

// 遍历BVH并求交, 需要事先构建好BVH树
// 所得交点是光线与最近物体的交点
Intersect(Ray ray, BVH node) {
    if(ray misses node.bbox) return; // 光线与包围盒不相交

    // 此时, 当前光线与node代表的包围盒相交
    // 进一步与node内所有物体求交, 并返回最近的交点(参数t最小)
    if (node is a leaf node) {
        test intersection with all objs;
        return closest intersection;
    }

    // 内部节点, 递归求交光线与其交点
    hit1 = Intersect(ray, node.child1);
    hit2 = Intersect(ray, node.child2);
    // 返回2个子节点中最近的交点
    return the closer of hit1, hit2;
}

空间划分 vs 物体划分

空间划分（如KD树）

  • 因为是按空间划分，所以空间不会重叠
  • 一个物体可能被多个区域包含

物体划分（如BVH）

  • 一组对象划分为不相交的子集，一个物体只会被一个区域包含
  • 每组（子集）的边界可能在空间上重叠

模拟相机的聚焦效果

需要为投影平面前的凸透镜（或相机的光圈）指定聚焦长度、其他参数，使有些对象能聚焦而另一些对象在交点之外.

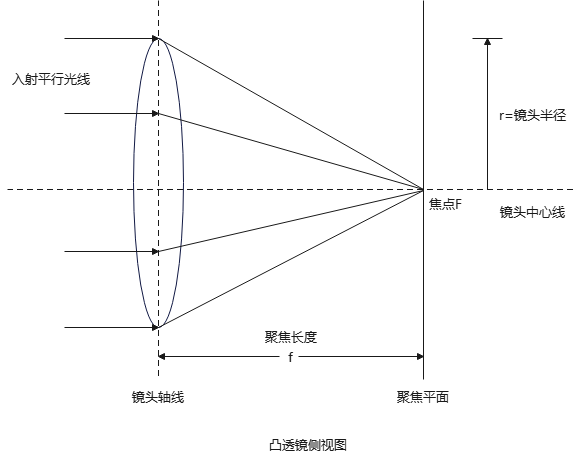
聚焦长度指从透镜中心到聚焦点F之间的距离，F是一组经过该透镜的平行线的汇聚点. 35mm相机的聚焦长度一般是50mm.

相机光圈常用参数n描述：

\[n=\frac{f}{2r} \]

其中，f称为f数或f刻度（光圈数），r是光圈半径.

典型的凸透镜侧视图：

img

光线追踪算法一般用薄透镜公式（thin-lens equation）：

\[\frac{1}{d}+\frac{1}{d_i}=\frac{1}{f} \]

其中，参数d是透视中心到一个对象的距离，\(d_i\)是透镜中心到聚焦该对象的图像平面的距离. 对象与其图像位于经过透镜中心的一条直线上、透镜的两侧，d>f.

也就是说，要讲距离透镜d的特定对象聚焦，可将像素平面置于透镜后\(d_i\)处.

img

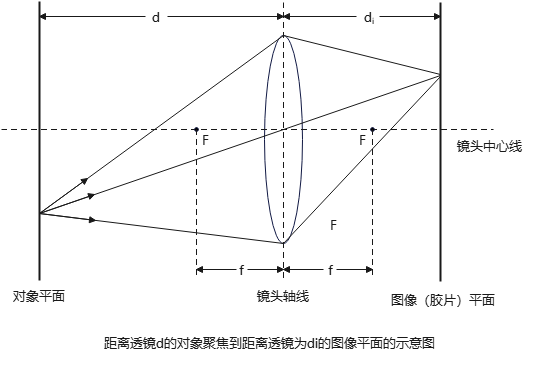
注意：透镜的焦点是平行光线垂直入射透镜后聚焦到一点，非垂直入射光线不一定落到焦点.

设场景中一对象距离透镜距离为d'，
如果d' ≠ d，则对象的投影点不会聚焦在图像平面；
如果d' > d，则该点聚焦到图像平面之前；
如果d' < d，则该点聚焦到图像平面之后.

位于d'的一个点（看作直径1）在图像平面上的投影近似一个小圆圈，称为模糊圆（the circle of confision），直径：

\[2r_c=\frac{|d'-d|f}{nd} \]

选择相机参数，使得一定距离范围内的模糊圆尺寸最小（\(2r_c\)最小），该距离范围称为相机的景深（depth of field）.

光线追踪反走样

走样：低频取样造成信息失真.

2种光线追踪反走样技术：过取样（super sampling）、适应性取样（adaptive sampling）.

  • 基本思想

将像素看成一个有限的正方形区域，而非单独的点.

1）过取样：在每个像素区域内，采用多束均匀排列的光线（取样点）；

2）适应性取样：在像素区域内，对一些部分采用不均匀排列的光线，也可用随机分布的光线.

当每个像素采用多束光线时，像素的光强通过区域内各束光线强度求平均得到.

一个简单的过取样示意图：

img

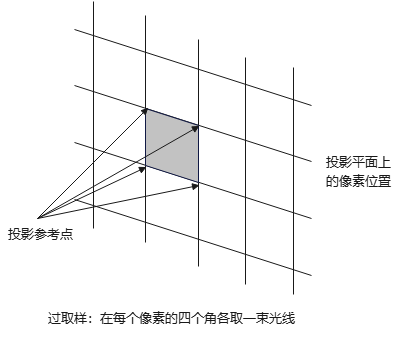
过取样在每个像素的4个角都生成一束光线，如果4束光线强度差异较大，或光线之间有小对象存在，则需将该像素区域进一步分割，并重复以上过程.

分割像素区域：比如可以用16束光线分割9个子区域，每束光线位于子像素的（4个）角点. 如下图：

img

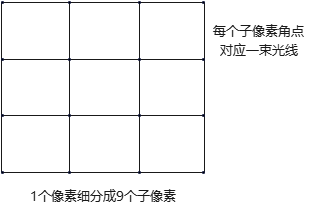
适应性取样对四角光束强度不相同（更严格）或有小对象的子像素进行细分，细分一直持续到每个子像素的光强近似相等或者每个像素中光束数达上限（如256）.

分布式光线追踪

分布式光线追踪（distributed ray tracing）：根据光照模型中多种参数随机分布光线的取样方法.

光照参数：像素区域、反射、折射方向、相机镜头区域、时间等.

分布式光线追踪，主要提供对物体表面光照准确描述时所需的多重积分的Monte Carlo（蒙特卡洛）估计值.

随机分布光线缺点：
像素平面随机分布光线，可实现像素区域，但完全随机的光线位置可能导致像素内部分区域出现密集光束，而另一部分却未经取样.

  • 像素区域抖动

解决办法：在规则子像素网格上，采用抖动（jitlering）技术，可获得像素区域内光束的较好的近似分布.

抖动：将一个像素区域划（单位正方形）分为16个子区域，在每个子区域内生成随机的抖动位置（jitler position）. 通过将每个子区域的中心坐标抖动一个小分量\(δ_x, δ_y(-0.5<δ_x, δ_y<0.5)\)来获得随机光线位置\((x+δ_x,y+δ_y)\)，将其作为中心坐标为(x,y)的单元内的光线位置.

img

  • 角域抖动

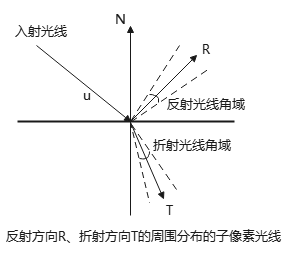
反射、透射（折射）路径也向空间范围分布. 为模拟表面光泽，对于不透明材质，可将在反射光线分布在理想反射方向R邻近区域. 将R的最大扩展区域分割为16个角域，每束反射光线在区域中心附近的抖动位置. Phong模型的\(\cos^{n_s}\phi\)可用来确定反射角度范围.

如果是透明材质，折射光线可沿着理想透视方向T进行抖动，从而得到分布式的折射光线.

img

小结

光线追踪技术，光学与各种物体表面求交.

基于包围盒的加速求交：空间划分，代表KD树；物体划分，代表BVH.

反走样技术：过取样、适应性取样.

分布式光线追踪利用像素区域抖动、角域抖动方法，解决随机分布光线存在的问题.

辐射度光照模型等其他全局光照技术，留待以后继续.

参考

GAMES101 Lecture13-14

算法（1）：KD树的原理与基本代码 | CSDN

posted @ 2024-01-10 18:03  明明1109  阅读(79)  评论(0)  编辑  收藏  举报