解析几何笔记：仿射坐标系

仿射坐标系
向量共线（共面）
空间直线和平面
参考

仿射坐标系

不共面向量

定理1 空间中任意给定三个不共面的向量\(\bm{e_1},\bm{e_2},\bm{e_3}\)，则任意一个向量\(\bm{m}\)可以唯一表示成\(\bm{e_1},\bm{e_2},\bm{e_3}\)的线性组合.

证明：
可表性.
取一点O，作\(\overrightarrow{OA_1},\overrightarrow{OA_2},\overrightarrow{OA_3}\)分别表示\(\bm{e_1},\bm{e_2},\bm{e_3},\bm{m}\). 过M作直线\(MN//\overrightarrow{OA_3}\)交平面\(OA_1A_2\)于点N，过N作直线\(NP//OA_1\)交\(OA_2\)于P.

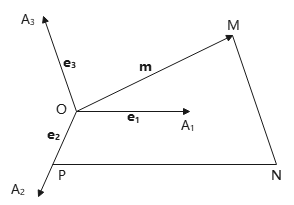
有，

\[\overrightarrow{OA_1}=\bm{e_1},\overrightarrow{OA_2}=\bm{e_2},\overrightarrow{OA_3}=\bm{e_3}, \\ \overrightarrow{OP}//\bm{e_1}, \overrightarrow{PN}//\bm{e_2}, \overrightarrow{NM}//\bm{e_3} \]

∴存在实数x,y,z使得

\[\overrightarrow{OP}=x\bm{e_1},\overrightarrow{PN}=y\bm{e_2},\overrightarrow{NM}=z\bm{e_3} \]

而

\[\bm{m}=\overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{PN}+\overrightarrow{NM}=x\bm{e_1}+y\bm{e_2}+z\bm{e_3} \]

唯一性. 如果存在另一组实数\(x_1,y_1,z_1\)，使得

\[m=\overrightarrow{OM}=x_1\bm{e_1}+y_1\bm{e_2}+z_1\bm{e_3} \]

则有，

\[(x-x_1)\bm{e_1}+(y-y_1)\bm{e_2}+(z-z_1)\bm{e_3}=0 \]

∵\(\bm{e_1},\bm{e_2},\bm{e_3}\)不共面
∴不存在非零实数\(\alpha,\beta,\gamma\)使得\(\alpha\bm{e_1}+\beta\bm{e_2}+\gamma\bm{e_3}=0\)成立
也就是说，\(\alpha=\beta=\gamma=0\)
∴\(x-x_1=y-y_1=z-z_1=0\)
∴\(x=x_1,y=y_1,z=z_1\)

基向量

定义1 空间中任意三个有次序的不共面的向量\(\bm{e_1},\bm{e_2},\bm{e_3}\)称为空间中的一组基. 对于空间中任一向量\(\bm{m}\)，若

\[\bm{m}=x\bm{e_1}+y\bm{e_2}+z\bm{e_3} \]

则把有序三元实数组(x,y,z)称为\(\bm{m}\)在基\(\bm{e_1},\bm{e_2},\bm{e_3}\)中的坐标.

如3D笛卡尔坐标系下，基向量可以是\(\bm{e_1}=(1,0,0),\bm{e_2}=(0,1,0)\bm{e_3}=(0,0,1)\). 空间中向量\(\bm{m}=10\bm{e_1}+20\bm{e_2}+30\bm{e_3}\)，可以用三元数组(10,20,30)来表示.

仿射标架（仿射坐标系）

定义2 空间中一个点O和一组基\(\bm{e_1},\bm{e_2},\bm{e_3}\)合在一起称为空间的一个仿射标架或仿射坐标系，记作\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)，其中O称为原点. 对于空间中任一点M，把它的定位向量\(\overrightarrow{OM}\)在基\(\bm{e_1},\bm{e_2},\bm{e_3}\)中的坐标称为点M在仿射标架\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)中的坐标.

简单说，原点 + 基 = 仿射标架（或仿射坐标系）

由定义知，点M在仿射坐标系\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)下坐标为(x,y,z)的充要条件：

\[\overrightarrow{OM}=x\bm{e_1}+y\bm{e_2}+z\bm{e_3} \]

\(\bm{m}\)在基\(\bm{e_1},\bm{e_2},\bm{e_3}\)中的坐标，也称为\(\bm{m}\)在仿射坐标系\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)中的坐标.

坐标轴

设\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)为一个仿射标架，过原点O且分别以\(\bm{e_1},\bm{e_2},\bm{e_3}\)为方向的有向直线分别称为x轴，y轴，z轴，它们统称坐标轴. 每2个坐标轴决定的平面称为坐标平面，分别是xOy, yOz, zOx平面. 坐标平面将空间分为8部分，称为八个挂限（注：2D平面是象限），每个挂限内，点的坐标符号不变.

直角标架（直角坐标系）

定义3 如果单位向量\(\bm{e_1},\bm{e_2},\bm{e_3}\)两两垂直，则\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)称为一个直角标架或直角坐标系.

注意：此时\(\bm{e_1},\bm{e_2},\bm{e_3}\)必不共面.

直角标架是一个特殊的仿射标架. 点或向量在直接坐标系中的坐标，称为直角坐标，在仿射坐标系中的坐标称为仿射坐标.

向量共线（共面）

注：由于仿射标架下很多结论证明依赖于这部分，因此将其加入本文.

向量的加法、数量乘法（向量乘以实数）统称线性运算.

设\(\bm{a_1,a_2,...,a_n}\)是一组向量，\(k_1,k_2,...,k_n\)是一组实数，则\(k_1\bm{a_1}+k_2\bm{a_2}+...+k_n\bm{a_n}\)是一个向量，称它为向量组\(\bm{a_1,a_2,...,a_n}\)的一个线性组合，称\(k_1,k_2,...,k_n\)是这个组合的系数.

定义4 向量组如果用同一起点的有向线段表示后，它们在一条直线（一个平面）上，则称这个向量组是共线（共面）的.

如果向量\(\bm{a}\)与\(\bm{b}\)共线，记作\(\bm{a}//\bm{b}\).

有以下结论：
1）\(\bm{0}\)向量与任意向量共线；
2）共线的向量组一定共面；
3）如果\(\bm{a}=\lambda\bm{b}\)，则\(\bm{a,b}\)共线.

两向量共线

命题1 如果\(\bm{a,b}\)共线，且\(\bm{a}\neq 0\)，则存在唯一实数使得\(\bm{b}=\lambda\bm{a}\).

证明：存在性.
如果\(\bm{a,b}\)同向，则对应单位向量\(\bm{b^0}=\bm{a^0}\)，进而由：

\[\bm{b}=|\bm{b}|\bm{b^0}=|\bm{b}|\bm{a^0}=|\bm{b}|(|\bm{a}|^{-1}\bm{a})=(|\bm{b}||\bm{a}|^{-1})\bm{a} \]

可取\(\lambda=|\bm{b}||\bm{a}|^{-1}\)，可得\(\bm{b}=\lambda\bm{a}\).
如果\(\bm{a,b}\)反向，则对应单位向量\(\bm{b^0}=-\bm{a^0}\)，也可得到类似结论.

唯一性.
假设\(\bm{b}=\lambda \bm{a}=\mu \bm{a}\)，则\((\lambda-\mu)\bm{a}=0\)
∵\(\bm{a}\neq 0\)
∴\(\lambda-\mu=0\)
∴\(\lambda=\mu\)

命题2 \(\bm{a,b}\)共线充要条件：存在不全为0的实数λ、μ，使得

\[\lambda \bm{a}+\mu \bm{b}=0 \]

证明：必要性.
设\(\bm{a,b}\)共线
如果\(\bm{a}=\bm{b}=0\)，可取\(\lambda=1,\mu=1\)，则\(1\bm{a}+1\bm{b}=0\).
如果\(\bm{a,b}\)不全为0，不妨设\(\bm{a}\neq 0\)，则存在实数λ使得\(\bm{b}=\lambda\bm{a}\). 有

\[\lambda \bm{a} + (-1)\bm{b}=0 \]

充分性.
如果有不全为0的实数λ、μ使得\(\lambda \bm{a}+\mu \bm{b}=0\)成立.
不妨设\(\bm{a}\neq 0\)，则\(\bm{a}=-\frac{\mu}{\lambda}\bm{b}\)
∴\(\bm{a,b}\)共线

推论1 \(\bm{a,b}\)不共线的充要条件：要使得式\(\lambda\bm{a}+\mu\bm{b}=0\)成立，则\(\lambda=\mu=0\).

证明：
必要性. 设\(\bm{a,b}\)不共线.
反证法：如果存在λ、μ不全为0，使得\(\lambda\bm{a}+\mu\bm{b}=0\)成立，那么上面定理，知\(\bm{a,b}\)共线. 这与假设茅盾，因此\(\lambda=\mu=0\).

充分性. 设\(\lambda\bm{a}+\mu\bm{b}=0\)成立时，必有\(\lambda=\mu=0\).
反证法：假设\(\bm{a,b}\)共线
当\(\bm{a}\)是0向量时，μ必为0，但λ可以是任意值，不符合必有\(\lambda=\mu=0\)的结论；
同理，当\(\bm{b}\)是0向量时，也不符合结论.
当\(\bm{a},\bm{b}\)都不是0向量时，那么存在实数γ，使得\(a=γb\)，即\(1\bm{a}+(-γ)\bm{b}=0\)，可取\(\lambda=1,\mu=-γ\)不符合结论.

因此，假设不成立，也就是\(\bm{a,b}\)不共线成立.

三向量共面

命题3 如果\(\bm{c}=\lambda\bm{a}+\mu\bm{b}\)，则\(\bm{a,b,c}\)共面.

证明：
如果\(\bm{a}\parallel\bm{b}\)，则\(\bm{a,b,c}\)共线，从而共面.
如果\(\bm{a}\nparallel\bm{b}\)，
当\(\lambda或\mu\)为0时，则\(\bm{c}\)必与\(\bm{b}或\bm{a}\)共线

当\(\lambda>0,\mu>0\)时，\(\bm{c}\)是以\(\lambda\bm{a}, \mu\bm{b}\)为邻边的平行四边形对角线
∴\(\bm{a,b,c}\)共面

当\(\lambda>0,\mu<0\)时，\(\bm{c}\)是以\(\lambda\bm{a}, (-\mu)(-\bm{b})\)为邻边的平行四边形对角线
∴\(\bm{a,b,c}\)共面
其他符号情况，可类似讨论.

命题4 如果\(\bm{a,b,c}\)共面，且\(\bm{a,b}\)不共线，则存在唯一实数对λ、μ，使得\(\bm{c}=\lambda \bm{a}+\mu \bm{b}\).

证明：
存在性.
从同一起点O作

\[\overrightarrow {OA}=\bm{a},\overrightarrow{OB}=\bm{b},\overrightarrow{OC}=\bm{c} \]

过点C作CD//OB交OA于D点.

∵\(\overrightarrow{OD}//\bm{a}\)
∴存在实数λ使得\(\overrightarrow{OD}=\lambda\bm{a}\)
同理，存在实数μ使得\(\overrightarrow{DC}=\mu\bm{b}\)
∴\(\bm{c}=\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{DC}=\lambda \bm{a}+\mu \bm{b}\).

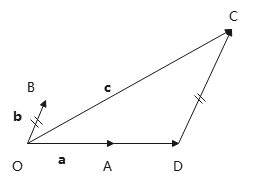
唯一性.
假设\(\bm{c}=\lambda\bm{a}+\mu\bm{b}=\lambda_1\bm{a}+\mu_1\bm{b}\)，则

\[(\lambda-\lambda_1)\bm{a}+(\mu-\mu_1)\bm{b}=0 \]

∵\(\bm{a,b}\)不共线
∴\(\lambda-\lambda_1=\mu-\mu_1=0\)
∴\(\lambda=\lambda_1,\mu=\mu_1\)

命题5 \(\bm{a,b,c}\)共面的充要条件：有不全为0的实数\(k_1,k_2,k_3\)，使得\(k_1\bm{a}+k_2\bm{b}+k_3\bm{c}=0\).

证明：充分性.
不妨设\(k_3\neq 0\)
有

\[\bm{c}=\frac{k_1}{k_3}\bm{a}+\frac{k_2}{k_3}\bm{b} \]

由命题3知，\(\bm{a,b,c}\)共面.

必要性.
如果\(\bm{a,b}\)共线，由命题2知，有不全为0的实数λ、μ，使得\(\lambda \bm{a}+\mu\bm{b}=0\)，那么\(\lambda \bm{a}+\mu\bm{b}+0 \bm{c}=0\).

如果\(\bm{a,b}\)不共线，由命题4知，存在唯一实数对λ、μ，使得\(c=\lambda \bm{a}+\mu\bm{b}\)，那么\(\lambda \bm{a}+\mu\bm{b}+(-1)\bm{c}=0\).（-1不等于0）

推论1 \(\bm{a,b,c}\)不共面的充要条件：从式\(k_1\bm{a}+k_2\bm{b}+k_3\bm{c}=0\)，可以推出\(k_1=k_2=k_3=0\).

证明：必要性. \(\bm{a,b,c}\)不共面.
反证法.
假设\(k_1,k_2,k_3\)不全为0时\(k_1\bm{a}+k_2\bm{b}+k_3\bm{c}=0\)成立，则由命题5，\(\bm{a,b,c}\)共面. 这与\(\bm{a,b,c}\)不共面条件茅盾，因此\(k_1,k_2,k_3\)必全为0.

充分性. \(k_1\bm{a}+k_2\bm{b}+k_3\bm{c}=0\)成立时，\(k_1=k_2=k_3=0\)
反证法.
假设\(\bm{a,b,c}\)共面，由命题5，\(k_1,k_2,k_3\)必不全为0. 这与\(k_1=k_2=k_3=0\)茅盾，因此\(\bm{a,b,c}\)必共面.

tips：该推论是命题5的逆否命题.

应用

例1 点M在线段AB上的充要条件：存在非负实数λ、μ使得\(\overrightarrow{OM}=\lambda \overrightarrow{OA}+\mu\overrightarrow{OB}且λ+μ=1\)，其中O是任意取的一点.

证明：必要性.
∵点M在线段AB上
∴\(\overrightarrow{AM},\overrightarrow{AB}\)同向
有\(\overrightarrow{AM}=k\overrightarrow{AB},0\le k \le 1\)
任取一点O，有

\[\overrightarrow{AM}=\overrightarrow{OM}-\overrightarrow{OA}=k\overrightarrow{AB}=k(\overrightarrow{OB}-\overrightarrow{OA})\\ \implies \overrightarrow{OM}=(1-k)\overrightarrow{OA}+k\overrightarrow{OB} \]

可取λ=1-k，μ=k，则λ+μ=1且λ≥0，μ≥0.

充分性.
如果存在非负实数λ、μ使得\(\overrightarrow{OM}=\lambda \overrightarrow{OA}+\mu\overrightarrow{OB}且λ+μ=1\)，其中O是任取的一点. 那么，有

\[\begin{aligned} \overrightarrow{AM}&=\overrightarrow{OM}-\overrightarrow{OA}\\ &=\lambda \overrightarrow{OA}+\mu \overrightarrow{OB}-\overrightarrow{OA}\\ &=(\lambda-1)\overrightarrow{OA}+\mu\overrightarrow{OB}\\ &=-\mu\overrightarrow{OA}+\mu\overrightarrow{OB}\\ &=\mu(\overrightarrow{OB}-\overrightarrow{OA})\\ &=\mu \overrightarrow{AB} \end{aligned} \]

∴\(\overrightarrow{AM},\overrightarrow{AB}\)共线，M在直线AB上
又\(0\le \mu \le 1\)
∴M在线段AB上

tips：该命题是线性坐标插值，坐标证明方式见数学基础：三角形重心坐标插值公式的证明

例2 A、B、C三点共线充要条件：存在不全为0的实数\(\lambda、\mu、\nu\)使得\(\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}+\nu\overrightarrow{OC}=0且\lambda+\mu+\nu=0\)，其中O是任取的一点.

证明：必要性.
设A、B、C共线.
则\(\overrightarrow{AB},\overrightarrow{AC}\)共线
∴存在不全为0的实数k,l使得\(k\overrightarrow{AB}+l\overrightarrow{AC}=0\)（命题2）
∴

\[k\overrightarrow{AB}+l\overrightarrow{AC}=k(\overrightarrow{OB}-\overrightarrow{OA})+l(\overrightarrow{OC}-\overrightarrow{OA})=-(k+l)\overrightarrow{OA}+k\overrightarrow{OB}+l\overrightarrow{OC} \]

可取\(\lambda=-(k+l),\mu=k,\nu=l\)，于是有

\[\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}+\nu\overrightarrow{OC}=0且\lambda+\mu+\nu=0 \]

充分性.
设存在不全为0的实数\(\lambda、\mu、\nu\)使得\(\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}+\nu\overrightarrow{OC}=0且\lambda+\mu+\nu=0\).
则有，

\[\begin{aligned} -(\mu+\nu)\overrightarrow{OA}+\mu\overrightarrow{OB}+\nu\overrightarrow{OC}&=0\\ \mu(\overrightarrow{OB}-\overrightarrow{OA})+\nu(\overrightarrow{OC}-\overrightarrow{OA})&=0\\ \mu \overrightarrow{AB}+\nu\overrightarrow{AC}&=0 \end{aligned} \]

∵\(\lambda,\mu,\nu\)不全为0且\(\lambda+\mu+\nu=0\)
∴\(\mu,\nu\)不全为0
∴\(\overrightarrow{AB},\overrightarrow{AC}\)共线
∴A、B、C三点共线.

仿射标架下的三点共线条件

定理2 在三个点A,B,C所在的平面上取一个仿射标架\([O;\bm{e_1,e_2}]\)，设A,B,C坐标分别为\((x_1,y_1),(x_2,y_2),(x_3,y_3)\)，则A、B、C三点共线充要条件：

\[\begin{vmatrix} x_1 & x_2 & x_3\\ y_1 & y_2 & y_3\\ 1 & 1 & 1 \end{vmatrix}=0 \]

证明：
行列式较为复杂，先将行列式简化下. 由于行列式将第i行（或列）乘以常数，然后再加到第j行（或列），行列式值不变，有

\[\begin{vmatrix} x_1 & x_2 & x_3\\ y_1 & y_2 & y_3\\ 1 & 1 & 1 \end{vmatrix} =\begin{vmatrix} x_1-x_3 & x_2-x_3 & x_3\\ y_1-y_3 & y_2-y_3 & y_3\\ 0 & 0 & 1 \end{vmatrix} =\begin{vmatrix} x_1-x_3 & x_2-x_3\\ y_1-y_3 & y_2-y_3 \end{vmatrix} \]

必要性.
设A、B、C三点共线.
则\(\overrightarrow{CA},\overrightarrow{CB}\)共线
∴存在不全为0的实数λ、μ使得\(\lambda \overrightarrow{CA}+\mu \overrightarrow{CB}=0\)
该式写成坐标形式：

\[\begin{cases} \lambda(x_1-x_3)+\mu(x_2-x_3)=0\\ \lambda(y_1-y_3)+\mu(y_2-y_3)=0 \end{cases} \]

关于x、y的齐次线性方程组：

\[\begin{cases} x(x_1-x_3)+y(x_2-x_3)=0\\ x(y_1-y_3)+y(y_2-y_3)=0 \end{cases} \]

有非零解\(x=\lambda,y=\mu\)的充要条件为系数矩阵的行列式为0（见余胜春编《线性代数》.2009 P102推论2），即

\[\begin{vmatrix} x_1-x_3 & x_2-x_3\\ y_1-y_3 & y_2-y_3 \end{vmatrix}=0 \]

充分性.
设行列式值为0，说明上面的齐次线性方程组有非零0解：\(x=\lambda,y=\mu\)，可使得\(\lambda \overrightarrow{CA}+\mu \overrightarrow{CB}=0\)
此时，A、B、C共线.

定理3 设向量\(\bm{a,b}\)在空间仿射标架\([O;\bm{e_1,e_2,e_3}]\)中坐标分别是\((a_1,a_2,a_3),(b_1,b_2,b_3)\). 则\(\bm{a,b}\)共线充要条件：

\[\begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix} =\begin{vmatrix} a_1 & b_1\\ a_3 & b_3 \end{vmatrix} =\begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix} =0 \]

证明：必要性.
设\(\bm{a,b}\)共线.
当\(\bm{a}=0\)时，结论显然成立.
当\(\bm{a}\neq 0\)时，存在实数λ使得\(\bm{b}=\lambda\bm{a}\)，有，

\[b_i=\lambda a_i,i=1,2,3 \]

进而有

\[\begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix} =\begin{vmatrix} a_1 & ka_1\\ a_2 & ka_2 \end{vmatrix}=0 \]

同理，

\[\begin{vmatrix} a_1 & b_1\\ a_3 & b_3 \end{vmatrix} =\begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix} =0 \]

充分性.
设行列式值为0. 有

\[\begin{cases} \begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix} =a_1b_2-a_2b_1=0\\ \begin{vmatrix} a_1 & b_1\\ a_3 & b_3 \end{vmatrix} =a_1b_3-a_3b_1=0\\ \begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix} =a_2b_3-a_3b_2=0 \end{cases} \]

如果\(\bm{a,b}\)中有一个为0，则\(\bm{a,b}\)显然共线；
如果\(\bm{a,b}\)都不是0，不妨设\(a_1\neq 0, b_1\neq 0\)（其他情况类似）

有

\[\begin{cases} b_2=\frac{b_1}{a_1}a_2\\ b_3=\frac{b_1}{a_1}a_3\\ a_2b_3=a_3b_2 \end{cases} \]

令\(k=\frac{b_1}{a_1}\)
∴\(\bm{b}=(b_1,b_2,b_3)=(b_1,\frac{b_1}{a_1}a_2,\frac{b_1}{a_1}a_3)=k(a_1,a_2,a_3)=k\bm{a}\)
∴\(\bm{a,b}\)共线.

线段的定比分点

这里从分点角度，对线性插值做了更详细描述，参见数学基础：三角形重心坐标插值公式的证明

对于线段AB（A≠B），如果点C满足\(\overrightarrow{AC}=\lambda \overrightarrow{CB}\)，则称点C分线段AB成定比λ.
当λ>0时，\(\overrightarrow{AC},\overrightarrow{CB}\)同向，点C是线段AB内部的点，称C为内分点；
当λ<0时，\(\overrightarrow{AC},\overrightarrow{CB}\)反向，C是线段AB外的一点，称C为外分点；
当λ=0时，C与A重合.
假如λ=-1，则\(\overrightarrow{AC}=-\overrightarrow{CB}\)，即\(\overrightarrow{AB}=0\)这与A≠B茅盾，因此λ≠-1.

命题6 设A、B坐标分别为\((x_1,y_1,z_1)、(x_2,y_2,z_2)\)，则分线段AB成定比λ（λ≠-1）的分点C坐标：

\[x=\frac{x_1+\lambda x_2}{1+\lambda},y=\frac{y_1+\lambda y_2}{1+\lambda},z=\frac{z_1+\lambda z_2}{1+\lambda} \]

证明：设C坐标(x,y,z)，则\(\overrightarrow{AC}=\lambda \overrightarrow{CB}\)，坐标形式：

\[\begin{cases} x-x_1=\lambda(x_2-x)\\ y-y_1=\lambda(y_2-y)\\ z-z_1=\lambda(z_2-z) \end{cases} \]

可得

\[x=\frac{x_1+\lambda x_2}{1+\lambda},y=\frac{y_1+\lambda y_2}{1+\lambda},z=\frac{z_1+\lambda z_2}{1+\lambda} \]

其中，\(\lambda=\frac{|\overrightarrow{AC}|}{|\overrightarrow{CB}|}\)

空间直线和平面

仿射坐标系中的平面

仿射坐标系下，如何表示一个平面？

我们知道，确定一个平面的条件（or）：
1）不在一条直线上的3个点；
2）一条直线+直线外一点；
3）2条相交直线；
4）2条平行直线.

为方便使用向量法，用1个点+2个不共线向量（相当于2条相交直线）确定一个平面.

问题转换为数学描述：
选定一个仿射标架\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\). 已知点\(M_0(x_0,y_0,z_0), \vec{v_1}=(X_1,Y_1,Z_1), \vec{v_2}=(X_2,Y_2,Z_2)\)，其中\(\vec{v_1},\vec{v_2}\)不共线. 现在要求点\(M_0\)和\(\vec{v_1},\vec{v_2}\)确定的平面π的方程.

点M(x,y,z)在平面π的充要条件：\(\overrightarrow{M_0M}\)与\(\bm{v_1}, \bm{v_2}\)共面.
∵\(\bm{v_1}\nparallel \bm{v_2}\)
∴\(\overrightarrow{M_0M},\bm{v_1},\bm{v_2}\)共面的充要条件为存在实数λ, μ使得：

\[\overrightarrow{M_0M}=\lambda v_1 + \mu v_2 \]

参数方程

用坐标形式（方程组）表示：

\[\begin{cases} x=x_0+\lambda X_1+\mu X_2, \\ y=y_0+\lambda Y_1+\mu Y_2, \\ z=z_0+\lambda Z_1+\mu Z_2 \end{cases} \]

上式称为平面π的参数方程，其中λ,μ称为参数，可以是任意实数.

tips：确定仿射标架后，再确定一个点M，如果它到原点的向量能用2个基向量线性表示，那么，该点M的集合就是基向量所确定的平面.

普通方程

由解析几何笔记：向量的外积中三向量共面条件知，向量\(\bm{a}(a_1,a_2,a_3),\bm{b}(b_1,b_2,b_3),\bm{c}(c_1,c_2,c_3)\)共面的充要条件混合积为0，即\(\bm{a}\times\bm{b}=\bm{c}\)，对应坐标表示：

\[\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}=0 \]

∴\(\overrightarrow{M_0M}\)与\(\bm{v_1}, \bm{v_2}\)共面的充要条件：

\[\begin{vmatrix} x-x_0 & X_1 & X_2\\ y-y_0 & Y_1 & Y_2\\ z-z_0 & Z_1 & Z_2 \end{vmatrix}=0 \]

按第1列展开后可得，

\[Ax+By+Cz+D=0 \]

其中，

\[A= \begin{vmatrix} Y_1 & Y_2\\ Z_1 & Z_2 \end{vmatrix}, B= -\begin{vmatrix} X_1 & X_2\\ Z_1 & Z_2 \end{vmatrix}, C= \begin{vmatrix} X_1 & X_2\\ Y_1 & Y_2 \end{vmatrix}, D=-(Ax_0+By_0+Cz_0) \]

上式称为平面的普通方程.

定理2 设平面π方程：\(Ax+By+Cz+D=0\)，则向量\(\bm{ω}(r,s,t)\)//π的充要条件：\(Ar+Bs+Ct=0\).

证明：
∵向量\(\bm{ω}\)//π, \(v_1,v_2\)位于平面π
∴\(\bm{ω,v_1,v_2}\)共面
根据三向量共面条件知，\(\bm{ω,v_1,v_2}\)共面充要条件：

\[\begin{vmatrix} r & X_1 & X_2\\ s & Y_1 & Y_2\\ t & Z_1 & Z_2 \end{vmatrix} \]

可得，

\[Ar+Bs+Ct=0 \]

思考：能否由平面π方程，得到平面上2个不共线向量？
答案是可以的. 下面进行推导.

平面π方程的方程中，A、B、C不能全为0，否则(x,y,z)可以任意取值，其集合就不是平面了. 不妨设A≠0，则有

\[r+\frac{B}{A}s+\frac{C}{A}t=0 \]

要求平面上2个不共线向量，也就是要得到2个不共线的向量\(\bm{ω_1,ω_2}\)满足上式.
不妨取\(\bm{ω_1}=(-\frac{B}{A},1,0),\bm{ω_2}=(-\frac{C}{A},0,1)\).

推论1 设平面π方程：\(Ax+By+Cz+D=0\)，则平面π//x轴（或y轴、z轴）的充要条件是A=0（或B=0、C=0）；平面π通过原点的充要条件是D=0.

证明：x轴+方向单位向量\(\bm{e_1}(1,0,0)\).
由定理2知，\(\bm{e_1}\)//平面π充要条件：

\[A\cdot 1+B\cdot 0+C\cdot 0=0\Leftrightarrow A=0 \]

同理，对于y轴（\(\bm{e_2}(0,1,0)\)）、z轴（\(\bm{e_3}(0,0,1)\)）也分别能得到类似结论：B=0、C=0.

下面证平面π通过原点的充要条件.
必要性：平面π通过原点\(O(0,0,0)\)
那么O必位于平面π方程，即\(A\cdot 0+B\cdot 0+C\cdot 0+D=0\implies D=0\)

充分性：D=0
有\(A\cdot 0+B\cdot 0+C\cdot 0+D=0\)
即原点\((0,0,0)\)位于平面π.

定理3 在空间中取定一个仿射坐标系，则平面的方程必定是三元一次方程；反之，任意一个三元一次方程表示一个平面.

证明：
前半部：
由前面平面的普通方程的推导，知平面的方程必定是形如\(Ax+By+Cz+D=0\)的三元一次方程.

后半部：
思路：用一个三元一次方程构造一个平面.
任意给定一个三元一次方程：\(A_1x+B_1y+C_1z+D_1=0\)，A、B、C不能同时为0，否则方程与x、y、z无关，就不是三元一次方程.

不妨设A≠0. 取点\(M_1(-\frac{D_1}{A_1},0,0)\)，取向量\(\bm{μ_1}(-\frac{B_1}{A_1},1,0),\bm{μ_2}(-\frac{C_1}{A_1},0,1)\).

显然，\(\bm{μ_1},\bm{μ_2}\)不共线（否则\(\bm{μ_1}//\bm{μ_2}\)）. 那么，由1点+2向量决定的平面方程为：

\[\begin{vmatrix} x-(-\frac{D_1}{A_1}) & -\frac{B_1}{A_1} & -\frac{C_1}{A_1}\\ y-0 & 1 & 0\\ z-0 & 0 & 1 \end{vmatrix}=0 \Leftrightarrow A_1x+B_1y+C_1z+D_1=0 \]

也就是说，方程\(A_1x+B_1y+C_1z+D_1=0\)对应由点\(M_1\)、向量\(\bm{μ_1},\bm{u_2}\)唯一决定的平面.

两平面的位置关系

两平面位置关系有3种：
1）相交于一条直线；
2）平行；
3）重合.ggggggggggggggg

已知平面方程，如何判定位置关系？

定理4 取定一个仿射标架，设2平面\(π_1,π_2\)方程分别为：

\[A_1x+B_1y+C_1z+D_1=0,\\ A_2x+B_2y+C_2z+D_2=0. \]

则
1）\(π_1,π_2\)相交的充要条件：方程的一次项系数不成比例；
2）\(π_1,π_2\)平行的充要条件：方程的一次项系数成比例，但常数项不与这些系数成比例；
3）\(π_1,π_2\)平行的充要条件：方程的所有系数成比例（包括常数项）.

证明：
充分性.
1）设\(π_1,π_2\)方程的一次项系数不成比例，则向量\(\bm{a_1}=(A_1,B_1,C_1),\bm{a_2}=(A_2,B_2,C_2)\)不共线.

因此，下面式子至少有一个成立

\[\begin{cases} \frac{A_1}{A_2}\neq \frac{B_1}{B_2}\\ \frac{A_1}{A_3}\neq \frac{B_1}{B_3}\\ \frac{A_2}{A_3}\neq \frac{B_2}{B_3} \end{cases} \]

写成行列式形式：

\[\begin{vmatrix} A_1 & B_1\\ A_2 & B_2 \end{vmatrix}\neq 0, \begin{vmatrix} A_2 & B_2\\ A_3 & B_3 \end{vmatrix}\neq 0, \begin{vmatrix} A_2 & B_2\\ A_3 & B_3 \end{vmatrix}\neq 0 \]

至少有一个行列式值不为0，否则\(\bm{a,b}\)共线（定理3）.

不妨设第一个行列式值不为0，则可令方程组z=0，可得到x、y的非齐次线性方程组：

\[\begin{cases} A_1x+B_1y+D_1=0\\ A_2x+B_2y+D_2=0 \end{cases} \]

线性方程组系数行列式不为0，即系数矩阵的秩R=2（R=n），则方程组有唯一解，设为\((x_0,y_0)\).
那么，\((x_0,y_0,0)\)就是\(π_1,π_2\)联立的方程组的解，这也是\(π_1,π_2\)在z=0时的唯一解.

z=0时，\(π_1\)方程变换为\(A_1x+B_1y+D_1=0\)，有无数个解（几何图形是一条直线），除了\((x_0,y_0,0)\)，其他点都不在\(π_2\)上，因此，两平面\(π_1,π_2\)既不是重合，又不是平行关系，只能是相交.

2）设方程组一次项系数成比例，但不包括常数项.
即存在实数λ≠0使得\((A_2,B_2,C_2)=\lambda(A_1,B_1,C_1)\)
代入\(π_1,π_2\)方程组：

\[\begin{cases} A_1x+B_1y+C_1z+D_1=0\\ \lambda A_1x+\lambda B_1y+\lambda C_1z+D_2=0 \end{cases} \]

可得

\[\frac{D_2}{\lambda}=D_1 \]

∵常数项不成比例
∴\(D_1\neq \frac{D_2}{\lambda}\)
∴方程组无解，即\(π_1,π_2\)平行

3）设方程组一次项系数成比例，包括常数项.
即存在实数λ≠0使得\((A_2,B_2,C_2,D_2)=\lambda(A_1,B_1,C_1,D_1)\)
代入\(π_1,π_2\)方程组：

\[\begin{cases} A_1x+B_1y+C_1z+D_1=0\\ \lambda (A_1x+B_1y+C_1z+D_1)=0 \end{cases} \]

可见两个方程的解完全相同，即\(π_1,π_2\)重合.

必要性. 反证法.
1）设\(π_1,π_2\)相交.
假设一次项系数成比例，则\(π_1,π_2\)平行或重合. 与条件矛盾，故只能相交.

2）3）证法类同.

三平面交于一点

命题7 设三个平面在仿射坐标系中方程分别为：

\[A_1x+B_1y+C_1z+D_1=0,\\ A_2x+B_2y+C_2z+D_2=0,\\ A_3x+B_3y+C_3z+D_3=0. \]

则三平面恰好交于一点的充要条件：

\[\begin{vmatrix} A_1 & B_1 & C_1\\ A_2 & B_2 & C_2\\ A_3 & B_3 & C_3 \end{vmatrix}\neq 0 \]

证明：
根据克拉默法则，方程组解有唯一解的充要条件是系数行列式不为零（见余胜春编《线性代数》.2009 P96），即