计算机图形：明暗处理

目录

• 多边形绘制算法
• 恒定强度的明暗处理
• Gouraud明暗处理
  • 概述
  • 线性插值公式
  • 增量法线性插值
• Phong明暗处理
  • 概述
  • 双线性插值求法向量
  • 增量法线性插值求法向量
• 快速Phong明暗处理
• OpenGL函数
• 小结
• 参考

多边形绘制算法

通常用多边形近似表示物体，多边形的表面绘制一般用扫描线实现. 而将光照模型应用于表面绘制，称为明暗处理. 明暗处理一般仅计算顶点的表面光强度，多边形面的其他位置通过插值得到. 因此，明暗处理又称为光亮度插值.

为解决多个平面近似表示的曲面物体的绘制物体问题，提出了不同的简便算法，典型有：Gouround光亮度插值、Phong向量插值.

恒定强度的明暗处理

恒定强度表面绘制（constant-intensity surface rendering）或平面绘制（flat surface rendering）：为所有投影点赋予相同的颜色 —— 将多边形表面一个顶点或中心点的光照模型应用于表面每个点，继而计算RGB三颜色分量.

已知平面上一点A的光强为\(I_A\)，恒定强度表面绘制模型下，平面上任一点B的光强\(I_B=I_A\).

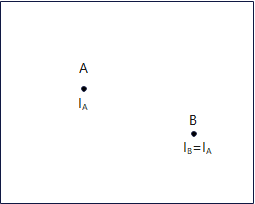
特点：快速、简单，快速生成一般曲面的大致外观. 但适用条件苛刻.

适用条件（and）：

1. 多边形是多面体的一个面，且不是一个近似表示曲面的多边形网的一部分；
2. 所有（照明该多边形的）光源离对象表面足够远，以至于N·L与衰减函数对于对象表面是各常数（见计算机图形：光照模型的Lambert漫反射模型、辐射强度衰减部分）；
3. 视点离该多边形足够远，以至于V·R对于多边形是一个常数.

注：N：物体表面单位法向量；L：入射点到光源的单位向量，N·L：入射角余弦值；V：入射点到视点的单位向量；R：反射光线的单位向量.

Gouraud明暗处理

概述

Gouraud表面绘制（Gouraud Surface rendering）又称光强度插值表面绘制（intensity-interpolation surface rendering）：将曲面表面的光亮度，取为近似表示该曲面的各个多边形顶点的双线性插值.

优点：光强度沿相邻多边形的公共边界均匀过渡，消除了在平面绘制中光强度不连续的现象.

缺点：表面高光有时会出现异常形状，如表面出现过亮或过暗的条纹，称为马赫带（Mach band）效应.

解决缺点的办法：1）使用更细小的多边形分割；2）使用其他明暗处理算法，如Phong明暗处理.

步骤：
1）确定每个多边形顶点处的平均单位法向量；
2）对每个顶点，应用光照模型计算光强度；
3）在多边形投影区域对顶点光强度进行线性插值；

对于1），求顶点单位法向量，常见空间曲线、曲面的法向量求解参见计算机图形：计算法向量.
例如，以A为公共顶点的4个相邻多边形的单位法向量分别为\(\bm{N_1、N_2、N_3、N_4}\)，则A点单位法向量：

\[\bm{N_A}=\frac{\bm{N_1+N_2+N_3+N_4}}{4} \]

tips: 计算顶点单位法向量前，需计算各多边形(面)法向量并单位化.

对于2），对顶点应用前面讲的光照模型，详见计算机图形：光照模型，计算光强.

对于3），在多边形绘制时，应用扫描线算法进行双线性插值：
例如，三角形\(V_1V_2V_3\)中，三顶点光强分别为\(I_1,I_2,I_3\). 一扫描线与三角形相交于A、B，P是投影于相应扫描线上一像素中心的多边形采样点，取A点光强\(I_A\)为\(I_1、I_2\)的线性插值，B点光强\(I_B\)为\(I_1、I_3\)的线性插值. 目的：求P点光强.

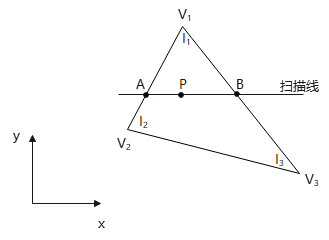
根据线段插值公式（参见数学基础：三角形重心坐标插值公式的证明），有，

\[\begin{cases} I_A=uI_1+(1-u)I_2, & u=\frac{AV_2}{V_1V_2}\\ I_B=vI_1+(1-v)I_3, & v=\frac{BV_2}{V_1V_3} \end{cases} \]

P点光强\(I_P\)为A、B两点的线性插值：

\[I_P=tI_A+(1-t)I_B, t=\frac{PB}{AB} \]

其中，u、v、t是插值参数.

为了计算u、v、t值，可先用y坐标算出A、B点对应的参数u、v，然后再用x坐标算出P点对应的参数t，即

\[u=\frac{y_A-y_2}{y_1-y_2},\\ v=\frac{y_B-y_3}{y_1-y_3},\\ t=\frac{x_B-x_P}{x_B-x_A} \]

tips: A、B位于同一条扫描线=>\(y_A=y_B\).

线性插值公式

公式证明见数学基础：三角形重心坐标插值公式的证明.

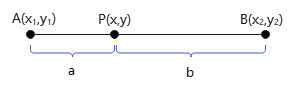
设点P是线段AB的插值点，\(|AP|=a,|BP|=b\)，有

\[P=uA+(1-u)B,u=\frac{b}{a+b} \]

写成坐标列向量形式：

\[\begin{pmatrix} x\\y \end{pmatrix} =u\begin{pmatrix} x_1\\y_1 \end{pmatrix} +(1-u)\begin{pmatrix} x_2\\y_2 \end{pmatrix},u=\frac{b}{a+b} \]

增量法线性插值

如果对扫描线上每个像素点都应用线性插值求光强，无疑带来大量运算. 可以用增量法，沿着扫描线从左到右计算线段AB上所有像素点的光强. 对每个像素点，仅用一次加法运算.

先说结论. 设\(I_A,I_B\)已确定，点\(P_1,P_2\)是扫描线上相邻2像素点，相邻像素的插值参数差为Δt，则\(P_2\)处光强\(I_{P2}\)与\(P_1\)处光强\(I_{P1}\)关系：

\[I_{P2}=I_{P1}+(I_A-I_B)Δt=I_{P1}+ΔI \]

其中，\(ΔI\)在同一条扫描线上为常数，即一条扫描线需计算一次.

下面证明该关系式：

∵\(P_1,P_2\)是线段AB的插值
∴

\[\begin{cases} I_{P1}=u_1I_A+(1-u_1)I_B,&u_1=\frac{P_1B}{AB}=\frac{x_B-x_{P1}}{x_B-x_A}\space (Ⅰ)\\ I_{P2}=u_2I_A+(1-u_2)I_B,&u_2=\frac{P_2B}{AB}=\frac{x_B-x_{P2}}{x_B-x_A}\space (Ⅱ) \end{cases} \]

其中，\(u_1,u_2\)是插值参数，取决于\(P_1,P_2\)对线段AB的分比.

\((Ⅱ)-(Ⅰ)\)可得，

\[I_{P2}-I_{P1}=(u_2-u_1)I_A-(u_2-u_1)I_B=(u_2-u_1)(I_A-I_B) \]

令\(Δt=u_2-u_1\)，则\(I_{P2}-I_{P1}=(I_A-I_B)Δt\)

问题转化为需证明：1）\(Δt\)是常数；2）\(I_A-I_B\)是常数.

∵\(P_1,P_2\)是同一条扫描线上相邻像素点
∴\(x_{P2}-x_{P1}=1\)是常数
∴\(Δt=u_2-u_1=\frac{1}{x_B-x_A}\)是常数

∵三角形是确定的，扫描线也是确定的
∴每条扫描线上的A、B点是确定的（相对于\(P_1,P_2\)点）
∴\(I_A,I_B\)是确定的(由2个方向上的一次线性插值得到)
∴\(I_A-I_B\)是确定的

故得证.

Phong明暗处理

概述

Phong表面绘制（Phong surface rendering），又称法向量插值绘制（normal-vector interpolation rendering）：对多边形顶点处法向量进行插值，取代光强度插值.

优点：多边形内部法向量变化连续，光强度更精确计算、更真实的表面高光显示，能有效解决马赫带效应问题.
缺点：需要比Gouraud更多的计算.

tips：时间换真实感效果.

类似于Gouraud明暗处理的光强度插值，法向量插值也能用基于扫描线的双线性插值法，求出多边形内扫描线上每个点的法向量，然后再应用光照模型求出各点光强度.

双线性插值求法向量

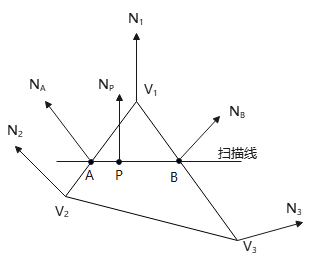
如上图，设3点\(V_1,V_2,V_3\)法向量\(N_1,N_2,N_3\)，则A点法向量\(N_A\)为\(N_1、N_2\)的线性插值，B点的法向量\(N_B\)为\(N_1、N_3\)的线性插值. P点法向量\(N_P\)是多少？

对A、B应用线性插值：

\[\begin{cases} N_A=uN_1+(1-u)N_2,& u=\frac{AV_2}{V_1V_2}\\ N_B=vN_1+(1-u)N_2,& v=\frac{BV_3}{V_1V_3} \end{cases} \]

再对P应用线性插值：

\[N_P=tN_A+(1-t)N_B,\space t=\frac{PB}{AB} \]

其中，u、v、t为插值参数.

增量法线性插值求法向量

在同一条扫描线上，对AB之间的像素点应用增量法求法向量：

\[N_{P2}=N_{P1}+(N_A-N_B)Δt=N_{P1}+ΔN \]

其中，\(P_1,P_2\)是从线段AB的相邻点，\(ΔN\)是相对于扫描线的常数.

快速Phong明暗处理

Phong明暗处理计算量大，可采用一些加速方法，有2类：数值法，几何法.

一种常用优化方法：隔一个像素应用光照模型，中间像素光强度取相邻像素的平均值.

另一种数值优化方法：将法向量插值公式代入光照模型，取泰勒展开式前3项近似作为光强度计算的公式. 也就是本文的快速Phong明暗处理.

快速Phong表面绘制（Fast Phong surface rendering)利用泰勒扩展式（Taylor series expansion）和三角形面片近似计算光强度.

三角形中，对任一点(x,y)的表面法向量N进行插值，可表示为：

\[\bm{N}=\bm{A}x+\bm{B}y+\bm{C} \]

其中，

\[\begin{aligned} \bm{A}&=a_1\bm{N_2}+a_2\bm{N_3-(a_1+a_2)}\bm{N_1}\\ \bm{B}&=b_1\bm{N_2}+b_2\bm{N_3-(b_1+b_2)}\bm{N_1}\\ \bm{C}&=c_1\bm{N_2}+c_2\bm{N_3-(1-c_1-c_2)}\bm{N_1} \end{aligned} \]

设\(\bm{L}\)是三角形面片的入射光线反向的向量（入射点指向点光源），则漫反射因子：

\[\begin{aligned} E_d(x,y)&=\frac{\bm{L}\cdot \bm{N}}{|\bm{L}| |\bm{N}|}\\ &=\frac{\bm{L}\cdot (\bm{A}x+\bm{B}y+\bm{C})}{|\bm{L}| |\bm{A}x+\bm{B}y+\bm{C}|}\\ &=\frac{\bm{L}\cdot \bm{A}x + \bm{L}\cdot \bm{B}y + \bm{L}\cdot \bm{C}}{|\bm{L}| |\bm{A}x+\bm{B}y+\bm{C}|}\\ &=\frac{ax+by+c}{\sqrt{dx^2+exy+fy^2+gx+hy+i}} \end{aligned} \]

其中，

\[\begin{aligned} a&=\frac{\bm{L}\cdot \bm{A}}{|\bm{L}|},B=\frac{\bm{L}\cdot \bm{B}}{|\bm{L}|},c=\frac{\bm{L}\cdot \bm{C}}{|\bm{L}|},\\ d&=\bm{A}\cdot \bm{A}, e=2(\bm{A}\cdot \bm{B}), f=\bm{B}\cdot \bm{B},\\ g&=2(\bm{A}\cdot \bm{C}),h=2(\bm{B}\cdot \bm{C}),i=(\bm{C}\cdot \bm{C}) \end{aligned} \]

将漫反射因子\(E_d(x,y)\)在(0,0)处按二元泰勒级数展开，取前三项，可得

\[E_d(x,y)=T_5x^2+T_4xy+T_3y^2+T_2x+T_1y+T_0 \]

其中，每个\(T_k\)都能用参数\(a,b...i\)表示.

\[\begin{aligned} T_5&=\frac{3ig^2-4cdi-4agi}{8i^2\sqrt{i}},T_4=\frac{3cgh-2cei-2bgi-2ahi}{4i^2\sqrt{i}},\\ T_3&=\frac{3ch^2-4cfi-4bhi}{8i^2\sqrt{i}},T_2=\frac{2ai-cg}{2i\sqrt{i}},\\ T_1&=\frac{2bi-ch}{2i\sqrt{i}},T_0=\frac{c}{\sqrt{i}} \end{aligned} \]

递推关系：假设屏幕上像素计算顺序为\((x_0,y_0),(x_1,y_1),...,(x_k,y_k),...,(x_{k+1}-x_{k}=l,y_{k+1}-y_{k}=l)\)，其中\(l\)是常数，那么，

\[E_d(x_{k+1},y_{k+1})=2E_d(x_k,y_k)-E_d(x_{k-1},y_{k-1})+T \]

其中，T是常数. 这样，计算每个像素的漫反射因子仅需要2次加法、1次移位运算.

同理，可根据\(E_s=\frac{\bm{N}\cdot\bm{H}}{|\bm{N}||\bm{H}|}\)求出镜面反射因子.

OpenGL函数

OpenGL使用常数强度表面绘制（也称平面绘制）或Gouraud表面绘制方法，显示表面. 没有Phong表面绘制、光线跟踪法或者辐射度方法的OpenGL函数，需要自行实现.

绘制方法：

glShadeModel(surfRenderingMethod);

surfRenderingMethod=GL_FLAT 指定常数强度表面绘制方法；
surfRenderingMethod=GL_SMOOTH 指定Gouraud表面绘制方法（默认）.

• 法向量

绘制多边形模拟对象时，需要指定法向量，从而用于计算多边形颜色.

glNormal3*(Nx, Ny, Nz);

例，对于平面绘制，一个三角形需要一个表面法向量

glNormal3fv(normalVector);
glBegin(GL_TRIANGLES);
    glVertex3fv(vertex1);
    glVertex3fv(vertex2);
    glVertex3fv(vertex3);
glEnd();

对于Gouraud表面绘制，需为每个顶点指定一个法向量

glBegin(GL_TRIANGLES);
    glNormal3fv(normalVector1);
    glVertex3fv(vertex1);
    glNormal3fv(normalVector2);
    glVertex3fv(vertex2);
    glNormal3fv(normalVector3);
    glVertex3fv(vertex3);
glEnd();

tips: 法向量不需要指定为单位向量，但所有表面法向量都是法向量可以减少计算量.

• 法向量规范化

将所有非单位向量转换为单位向量

glEnable(GL_NORMALIZE);

会对经过缩放或错切等几何变换的表面向量也起作用.

• 法向量列表

如果不想为每个表面（或顶点）单独指定法向量，可以用法向量列表：

glEnableClientState(GL_NORMAL_ARRAY);

glNormalPointer(dataType, offset, normalArray);

数据类型dataType可选项：GL_BYTE、GL_SHORT、GL_INT、GL_FLOAT（默认）、GL_DOUBLE. 根据数据类型，可推导出一个法向量占用多少byte，即数据类型占用字节数*3.

offset 给出数组normalArray中连续的法向量之间的字节数，默认值0，表示法向量是连续存储的，中间没有间断.

normalArray 指向数组中第一个法线的第一个坐标的指针.

小结

问题：计算多边形顶点法向量，是在投影前，还是投影后？

投影后. 因为只有投影到屏幕坐标后，三角形才可能与扫描线相交.

参考

彭群生.计算机真实感图形的算法基础[M].科学出版社,1999.