计算机图形：三维观察之基本概念

目录

• 三维观察概述
  • 三维场景观察
  • 投影
  • 深度提示
• 三维观察流水线
• 三维观察坐标系参数
  • 观察平面法向量N
  • 观察向上向量V
  • uvn观察坐标系
• 世界坐标系=>观察坐标系

该部分分2篇：1）三维观察之基本概念；2）三维观察之投影及变换。

三维观察概述

观察函数通过一组将对象的指定视图投影到显示设备表面上的过程，来处理对象的描述。三维观察一些处理，如裁剪子程序，与二维观察类似；但包含一些独有的任务，如投影子程序将场景变换到平面视图、识别可见部分、光照效果、表面特征等。

三维场景观察

为显示三维世界坐标场景，需：

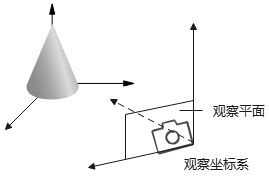
1. 先建立观察坐标系\(x_{view}y_{view}z_{view}\)。
2. 然后将对象描述变换到观察坐标系，并投影到观察平面上。

投影

有多种投影方法：

1. 平行投影（parallel projection）：沿平行方向投影每个点，将实体描述投影到观察平面。

2. 透视投影（perspective projection）：沿会聚路径投影每个点，将实体描述投影到观察平面。类似于人眼/照相机镜头获得图像的原理，有近大远小的效果。

深度提示

深度提示技术用于说明深度信息，可用于鉴别观察方向显示的对象中哪个在前、哪个在后。

深度提示技术：

1. 线框图中，按对象到观察位置的距离来改变线段的亮度，从而指示深度。
2. 在感觉对象的强度上模拟雾气效果。

三维观察流水线

建立三维场景、将场景变换到设备坐标（屏幕坐标）的一般步骤：

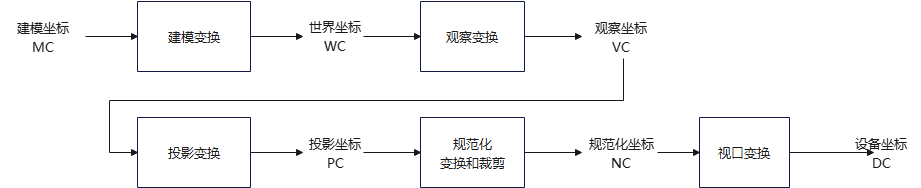
投影操作，将场景的观察坐标描述转换为投影平面的坐标位置。

投影变换后，建立三维裁剪区域，称为观察体（view volume），其形状、大小依赖于裁剪窗口的尺寸、投影方式和所选的观察方向的边界位置。

三维观察坐标系参数

观察坐标系是三维观察的重要环节。建立三维观察坐标系步骤：

1. 在世界坐标系中选定一点\(P_0=(x_0,y_0,z_0)\)作为观察原点（观察坐标系原点），称为观察点（view point）或观察位置（viewing position）。观察点也称为视点（eye position）或照相机位置（camera position）。
2. 指定决定\(y_{view}\)方向的观察向上向量（view-up-vector）V。
3. 指定另2个坐标轴方向：\(x_{view},z_{view}\)。

建立右手观察坐标系示意图：

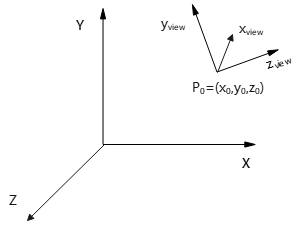
观察平面法向量N

观察方向\(\xrightarrow{}-z_{view}\xrightarrow{}N\).

观察方向通常沿\(-z_{view}\)方向，观察平面（view plane）也称投影平面（projection plane），一般假设观察平面与\(z_{view}\)轴垂直。而观察平面的方向（\(+z_{view}\)方向），定义为观察平面法向量（view plane normal vector）N。如下图：

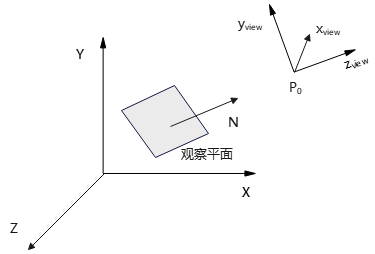
∵观察平面//\(x_{view}y_{view}\)平面(观察平面⊥\(z_{view}\)轴)

∴可用标量参数设定观察平面在\(z_{view}\)轴位置\(z_{vp}\)。

法向量N有多种指定方法：
1）从世界坐标系原点到某选定点的连线方向；
2）选定参考点\(P_{ref}\)到观察原点\(P_0\)的方向（注：OpenGL使用该方法）；
3）方向角定义。

参考点\(P_{ref}\)称为场景中的注视点（look-at point），观察方向与N方向相反。

注意：法向量参考点/注视点用于求观察平面的法向量，不是投影参考点\(P_{prp}\)，更不是观察原点。

观察向上向量V

观察向上向量\(V\times N\xrightarrow{}x_{view},x_{view}\times N\xrightarrow{}+y_{view}(v)\)

先选定与世界坐标系原点相关的一个位置来定义V，因此，V是从世界坐标系原点到选定点。
∵N代表\(z_{view}\)轴，而\(V⊥z_{view}\)
∴V⊥N

tips：V是与v,N共面的任意向量，只需确保V∦N，然后调整使其与N垂直。调整后为v。为方便，可选择V=(0,1,0)，即//世界坐标系\(y_{w}\)轴。

uvn观察坐标系

\(N\xrightarrow{}z_{view}\xrightarrow{}n, V\xrightarrow{}y_{view}\xrightarrow{}v, V\times N\xrightarrow{}x_{view}\xrightarrow{}u\)

UVN系统遵循右手规则，有

\[U=V\times N \]

∵U⊥N、V
∴U可作为\(+x_{view}\)方向

单位轴向量计算：

\[\tag{1} \begin{aligned} n&={N\over |N|}=(n_x,n_y,n_z)\\ u&={V\times n\over |V\times n|}=(u_x,u_y,u_z)\\ v&=n\times u=(v_x,v_y,v_z) \end{aligned} \]

u、v、n构成的坐标系，称为uvn观察坐标参考系统（uvn viewing-coordinate reference frame），如下图：

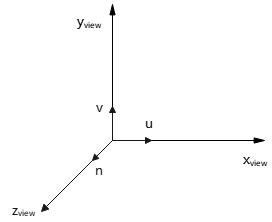
世界坐标系=>观察坐标系

如何将世界坐标系中对象描述，转换到观察坐标系中？

世界坐标系=>观察坐标系，对象的坐标变换分两步：
1）平移观察坐标系原点到世界坐标系原点；
2）旋转观察坐标系，让\(x_{view}, y_{view}, z_{view}\)轴对应到世界坐标系的\(x_w, y_w, z_w\)轴。

tips：坐标系的变换方向，与对象坐标的变换方向 相反。

步骤1，世界坐标系下\(P=(x_0,y_0,z_0)\)为观察坐标系原点，平移变换：

\[\tag{2} T=\begin{bmatrix} 1 & 0 & 0 & -x_0\\ 0 & 1 & 0 & -y_0\\ 0 & 0 & 1 & -z_0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

步骤2，
∵观察坐标系轴向量已知
∴可用观察坐标系的单位轴向量u、v、n来构造旋转矩阵
原理参见计算机图形：三维坐标系变换
旋转变换：

\[\tag{3} R=\begin{bmatrix} u_x & u_y & u_z & 0\\ v_x & v_y & v_z & 0\\ n_x & n_y & n_z & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

∴世界坐标系=>观察坐标系的复合变换矩阵：

\[\begin{aligned} M_{WC,VC}&=R\cdot T(-x_0,-y_0,-z_0)\\ &=\begin{bmatrix} u_x & u_y & u_z & -x_0u_x-y_0u_y-z_0u_z\\ v_x & v_y & v_z & -x_0v_x-y_0v_y-z_0v_z\\ n_x & n_y & n_z & -x_0n_x-y_0n_y-z_0n_z\\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

变换矩阵\(M_{WC,VC}\)的平移因子（最后一列前3行），可看作单位轴向量\(u=(u_x,u_y,u_z)、v=(v_x,v_y,v_z)、n=(n_x,n_y,n_z)\)与向量\(P_0=(x_0,y_0,z_0)\)的点积：

\[\tag{4} -u\cdot P_0=-x_0u_x-y_0u_y-z_0u_z\\ -v\cdot P_0=-x_0v_x-y_0v_y-z_0v_z\\ -n\cdot P_0=-x_0n_x-y_0n_y-z_0n_z \]

因此，更简洁写法：

\[\tag{5} \begin{aligned} M_{WC,VC}&=R\cdot T(-x_0,-y_0,-z_0)\\ &=\begin{bmatrix} u_x & u_y & u_z & -u\cdot P_0\\ v_x & v_y & v_z & -v\cdot P_0\\ n_x & n_y & n_z & -n\cdot P_0\\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

---