计算机图形：三维坐标系变换

目录

• 二维坐标系变换
  • 由旋转角进行坐标系转换
  • 构造旋转矩阵
    • 正交矩阵概念
    • 利用正交矩阵构造旋转矩阵
• 三维坐标系变换
  • 利用正交矩阵构筑旋转矩阵
  • 变换矩阵的推导
• 小结

将对象的描述从一个坐标系转换到另一个，在图形应用非常重要。本文主要从坐标的角度，探讨二维、三维空间下的对象如何从一个坐标系转换到另一个坐标系。

坐标系：除了笛卡尔坐标系，有极坐标、球面坐标、椭圆坐标等。这里仅考虑笛卡尔坐标系。

二维坐标系变换

由旋转角进行坐标系转换

坐标轴的正交变换：

\[\delta: A[\bm{e_1},\bm{e_2};O(0,0)]\xrightarrow{\begin{aligned}&1. 绕O逆时针旋转θ;\\&2. 平移至O'(x_0,y_0)\end{aligned}}B[\bm{e_1'},\bm{e_2'};O'(x_0,y_0)] \]

其中，\(\bm{e_1}=(1,0)^A,\bm{e_2=}(0,1)^A\)是A的基向量；\(\bm{e_1'}=(1,0)^B,\bm{e_2'}=(0,1)^B\)是B的基向量.

含义：2D空间下，2个坐标系：A为\(xy\)坐标系，B为\(x'y'\)坐标系。其中，\(xy\)系统原点\(O(0,0)^A\)，将其绕原点逆时针旋转θ角，然后平移至\(O'(x_0,y_0)^A\)处，得到\(x'y'\)坐标系。

---

tips：A系统下坐标，记为\((x,y)^A\)；B系统下坐标，记为\((x,y)^B\). 如果不注明，默认是A系统坐标.

---

问题：A系统任一点\(P(x,y)^A\)，如何转换到B系统的点\(P'(x', y')^B\)？

点的坐标转换与坐标轴的转换，方向相反，即

\[P\xrightarrow{复合变换M} P'\iff B \xrightarrow{复合变换M} A \]

于是，可分两步得到复合变换矩阵M：

1. T: 将\(O'(x_0,y_0)\)平移到\(O(0,0)\)；
2. R: 将\(x'\)轴顺时针旋转\(θ\)角与x轴重合。

步骤1平移矩阵：

\[\tag{1} T(-x_0,-y_0)=\begin{bmatrix} 1 & 0 & -x_0\\ 0 & 1 & -y_0\\ 0 & 0 & 1 \end{bmatrix} \]

步骤2旋转矩阵：

\[\tag{2} R_z(-θ)=\begin{bmatrix} \cosθ & \sinθ & 0\\ -\sinθ & \cosθ & 0\\ 0 & 0 & 1 \end{bmatrix} \]

注意：顺时针旋转取\(-θ\)。

于是，\(P(x,y)\xrightarrow{M_{xy,x'y'}} P'(x',y')\)的复合变换矩阵：

\[\tag{3} \begin{aligned} M_{xy,x'y'}&=R_z(-θ)\cdot T(-x_0,-y_0)\\ &= \begin{bmatrix} \cosθ & \sinθ & 0\\ -\sinθ & \cosθ & 0\\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -x_0\\ 0 & 1 & -y_0\\ 0 & 0 & 1 \end{bmatrix} \\ &=\begin{bmatrix} \cosθ & \sinθ & -(x_0\cosθ+y_0\sinθ)\\ -\sinθ & \cosθ & x_0\sinθ-y_0\cosθ\\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

这样，A系统坐标通过平移、旋转，得到B系统坐标。

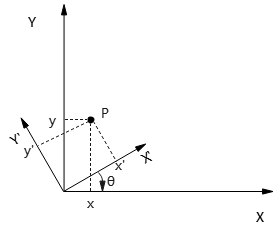
• 如何理解坐标轴的复合变换？

思考：上述复合变换中，明明\(x'y'\)坐标轴变换成了\(xy\)坐标轴，为什么\(xy\)系统转换成\(x'y'\)系统，而不是反过来？

用最简单的点\((0,0)\)来验证。假设\(x'y'\)系统下，原点坐标\((0,0)^B\)，那么在\(xy\)系统下坐标为\((x_0,y_0)^A\)，显然不符合复合变换；
而\(xy\)系统原点\((0,0)^A\)，在\(x'y'\)系统下，坐标为\((-(x_0\cosθ+y_0\sinθ),x_0\sinθ-y_0\cosθ)^B\)，符合复合变换。

求解\(O(0,0)^A\)在B系统下坐标示意图（注意加负号）：

经复合变换，\(P(x_p,y_p)^A\to P'(x_p',y_p')^B\)。

变换过程：

\[P'(x_p',y_p')^B=M_{xy,x'y'}P(x_p,y_p)^A=R_z(-θ)\cdot T(-x_0,-y_0)\cdot \begin{bmatrix} x_p\\y_p\\1 \end{bmatrix}^A \]

令\(x=x_p, y=y_p, x'=x_p', y'=y_p'\)，
那么，

\[\tag{4} P'(x',y')^B=R_z(-θ)\cdot T(-x_0,-y_0)\cdot P(x,y)^A \]

这样，就将\(xy\)系统坐标转换到了\(x'y'\)系统。

构造旋转矩阵

有时，我们并不知道旋转角θ值，而知道新的坐标轴方向（\(x',y'\)轴）。此时，可先求θ大小（向量点积），然后得到旋转矩阵. 这里要介绍另一种方法：构造旋转矩阵，该变换将坐标轴\(x'y'\)旋转到坐标轴\(xy\)，即将A系统坐标转换为B系统坐标。

正交矩阵概念

先复习几个概念：

• 正交向量

点积为0的两个或多个向量，称为正交向量。

假设向量\(V_1=(x_1,y_1), V_2=(x_2,y_2)\)是一组正交向量，则\(V_1\cdot V_2=x_1x_2+y_1y_2=0\)。
所谓正交向量，

• 正交矩阵

如果矩阵A，满足\(\bm{A}^T\bm{A}=E\)，则称A为正交矩阵。

对于正交矩阵，其行向量组（或列向量组）为单位向量且两两正交。这组行（或列）向量构成一个空间的基，称为规范正交基。
下面证明：
设A是一个列向量矩阵且为正交矩阵，\(A=(\bm{α_1},\bm{α_2},...,\bm{α_n})\)，其中\(\bm{α_i}(i=1,2,...,n)\)为列向量. 那么，

\[\begin{aligned} A^TA = \begin{bmatrix} \bm{α_1}^T\\ \bm{α_2}^T\\ ... \bm{α_n}^T \end{bmatrix} \begin{bmatrix} \bm{α_1},\bm{α_2},...,\bm{α_n} \end{bmatrix} &= E\\ \begin{bmatrix} \bm{α_1}^T\bm{α_1} & \bm{α_1}^T\bm{α_2} & ... & \bm{α_1}^T\bm{α_n}\\ \bm{α_2}^T\bm{α_1} & \bm{α_2}^T\bm{α_2} & ... & \bm{α_2}^T\bm{α_n}\\ ... & ... & ... & ...\\ \bm{α_n}^T\bm{α_1} & \bm{α_n}^T\bm{α_2} & ... & \bm{α_n}^T\bm{α_n} \end{bmatrix}&=\begin{bmatrix} 1 & 0 & ... & 0\\ 0 & 1 & ... & 0\\ ... & ... & ... & ...\\ 0 & 0 & ... & 1 \end{bmatrix} \end{aligned} \]

对于任意列向量\(\bm{α_i}, \bm{α_j}\)，
1）如果\(i=j\)，那么\(\bm{α_i}*\bm{α_j}=\bm{α_i}*\bm{α_i}=1 \implies |\bm{α_i}|=1\)；
2）如果\(i≠j\)，那么\(\bm{α_i}*\bm{α_j}=0\)，则\(\bm{α_i}, \bm{α_j}\)互为正交向量。

当A由行向量组成时，该结论依然成立。

利用正交矩阵构造旋转矩阵

已知向量\(\bm{V}\parallel y'\)轴，那么，\(y'\)轴单位向量：

\[\tag{5} \bm{v} = {V\over |V|}=(v_x,v_y)^A \]

将\(\bm{v}\)顺时针旋转90°，得到沿\(x'\)轴单位向量：

\[\tag{6} \begin{aligned} \bm{u} &= (u_x,u_y)\\ &=(v_y,-v_x) \end{aligned} \]

上式证明：
如下图
∵\(\bm{v}, \bm{u}\)都是单位向量
∴\(|\bm{v}|=|\bm{u}|=1\)
假设\(\bm{v}\)在第二象限，\(\bm{v}\)与y轴夹角\(α\)
∴\(\bm{v} = (-\cos α, \sin α), \bm{u} = (\sin α,\cos α)\)
∵\(\bm{v} = (v_x,v_y)\)
∴\(\bm{u}=(v_y,-v_x)\)，即得证.

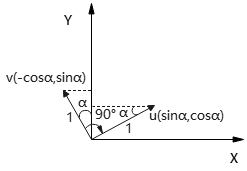
显然，\(\bm{v}, \bm{u}\)正交，即\(\bm{v}\cdot \bm{u}=0\iff v⊥u\)。

由(2)知，旋转矩阵\(R(-θ)\)的行向量组是一组正交单位向量（即一组规范正交基）：

\[R(-θ)=\begin{bmatrix} \cosθ & \sinθ & 0\\ -\sinθ & \cosθ & 0\\ 0 & 0 & 1 \end{bmatrix} \\ \]

i.e. 行向量组\((\cosθ, \sinθ, 0),(-\sinθ,\cosθ,0),(0,0,1)\)是一组规范正交基

问题：是否可以由一组规范正交基得到对应旋转矩阵？

答案是可以，可用规范正交基作为行向量（或列向量）组构造出旋转矩阵。不妨令，

\[\tag{7} R=\begin{bmatrix} u_x & u_y & 0\\ v_x & v_y & 0\\ 0 & 0 & 1 \end{bmatrix} \]

其中，\(v_x=-\sinθ,v_y=\cosθ\)。利用式(6)中\(\bm{u},\bm{v}\)的关系，可得\(u_x=v_y=\cosθ, u_y=-v_x=\sinθ\)，这符合旋转矩阵\(R(-θ)\)特性。

---

tips: 行向量组\(\bm{u}=(u_x,u_y),\bm{v}=(v_x,v_y)\)，对应左乘坐标（列向量）

\[\begin{aligned} P' &= \begin{pmatrix}\bm{u}\\\bm{v}\\\end{pmatrix}P\\ \begin{pmatrix}x' \\ y'\end{pmatrix} &= \begin{pmatrix}\bm{u}\\\bm{v}\\\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix}\\ \begin{pmatrix}x' \\ y'\end{pmatrix} &= \begin{pmatrix} xu_x+yu_y \\xv_x+yv_y \end{pmatrix} \end{aligned} \]

列向量组\(\bm{u}=\begin{pmatrix}u_x\\u_y\end{pmatrix},\bm{v}=\begin{pmatrix}v_x\\v_y\end{pmatrix}\)，对应右乘坐标（行向量）

\[\begin{aligned} P' &= P\begin{pmatrix}\bm{u} & \bm{v}\end{pmatrix}\\ \begin{pmatrix}x'&y'\end{pmatrix} &= \begin{pmatrix}x&y\end{pmatrix} \begin{pmatrix}\bm{u} & \bm{v}\end{pmatrix}\\ \begin{pmatrix}x' & y'\end{pmatrix} &= \begin{pmatrix}xu_x + yu_y \\ xv_x + yv_y\end{pmatrix} \end{aligned} \]

因此，旋转矩阵用行向量组，还是列向量组并无本质区别，可以看想变换的坐标用列向量形式，还是行向量形式.

---

接下来问题：\(θ\)在[0,2π)范围内是否有唯一解，即构造的旋转矩阵是否对应唯一的旋转？

答案是有唯一解。下面证明：
我们知道，正弦和余弦函数在0~2π范围内有2个解（如果有解），设2个解分别为\(θ_1,θ_2\in [0,2\pi)\)。

先根据\(\sinθ\)讨论\(θ\)取值范围，
1）当\(v_x<0\)时，\(\sinθ > 0\)，那么\(θ_1 \in [0,{\pi\over 2}), θ_2\in [{\pi\over 2}, \pi)\)；

2）当\(v_x\ge 0\)时，\(\sinθ \le 0\)，那么\(θ_1\in [\pi,{3\over 2}\pi), θ_2\in[{3\over 2}\pi, 2\pi)\)；

再根据\(\cosθ\)讨论\(θ\)取值范围，
1）当\(v_y>0\)，则\(θ_1\in[0,{\pi\over 2}),θ_2\in[{3\over 2}\pi, 2\pi)\)；
2）当\(v_y<0\)，则\(θ_1\in [{\pi\over 2},\pi),θ_2\in [\pi,{3\over 2}\pi)\)。

再综合sin、cos取值范围。不难发现，当sin、cos取值确定时，\(θ\)范围只能是长度为π/2的4个区间之一：\([0,{\pi \over 2}), [{\pi \over 2},\pi), [\pi,{3\over 2}\pi), [{3\over 2}\pi,2\pi)\)。
而sin、cos在这些区间连续且单调，因此有唯一解。

举例，如果\(y'\)轴方向向量\(\bm{v}=(-1,0)\)，那么\(x'\)轴方向向量\(\bm{u}\)应该在\(+y\)轴上（i.e. \(\bm{u}=(0,1)\)），且旋转矩阵为：

\[R=\begin{bmatrix} u_x & u_y & 0\\ v_x & v_y & 0\\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

而根据(2)，令\(θ={\pi\over 2}\)，也能得到同样的旋转矩阵。

tips：这里只考虑旋转矩阵，没有考虑平移。如果要求平移矩阵，还需要知道\(x'y'\)系统原点在\(xy\)系统中的位置。

• 正交矩阵R的含义

对于正交矩阵R，有

\[B[O';e_1',e_2',e_3']\xrightarrow{R}A[O;e_1,e_2,e_3]\iff P(x,y)^A\xrightarrow{R}P'(x',y')^B \]

R的每个行向量，刚好是B系统的坐标轴单位向量。

---

三维坐标系变换

利用正交矩阵构筑旋转矩阵

类似于二维坐标系变换，三维空间下，也能用一组规范正交基构造旋转矩阵。

问题描述：将\(xyz\)系统（A）下的坐标描述转换到\(x'y'z'\)坐标系统（B）。

步骤：
1）T: 先将\(x'y'z'\)原点平移到\(xyz\)原点；
2）R: 进行一系列旋转使得对应坐标轴重合。如果2个坐标系比例不同，需要先缩放使比例相同。

如下图：

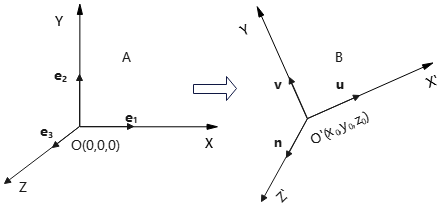
其中，\(\bm{u},\bm{v},\bm{n}\)分别为\(X', Y', Z'\)轴单位轴向量。B系统的原点\(O'\)在A系统的\((x_0,y_0,z_0)^A\)位置，坐标轴由\(xyz\)坐标轴旋转得到。

首先，将\(O'\)平移至\(O(0,0,0)^A\)，对应平移矩阵\(T(-x_0,-y_0,-z_0)\)。
三维平移、旋转、缩放操作，参见计算机图形：三维几何变换。

\[\tag{8} T(-x_0,-y_0,-z_0)=\begin{bmatrix} 1 & 0 & 0 & -x_0\\ 0 & 1 & 0 & -y_0\\ 0 & 0 & 1 & -z_0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

然后，用单位轴向量来构造坐标轴旋转矩阵，将单位轴向量\(\bm{u},\bm{v},\bm{n}\)分别转换到x、y、z轴上。构造方法类似于二维情形（参见(7)）。

\[\tag{9} R=\begin{bmatrix} u_x & v_x & n_x & 0\\ u_y & v_y & n_y & 0\\ u_z & v_z & n_z & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

其中，B系统\(X',Y',Z'\)轴单位向量\(\bm{u}=(u_x,u_y,u_z)^A, \bm{v}=(v_x,v_y,v_z)^A, \bm{n}=(n_x,n_y,n_z)^A\)。

于是，复合变换矩阵：

\[\tag{10} M_{xyz,x'y'z'}=R\cdot T(-x_0,-y_0,-z_0) \]

A系统\(P\)点\(\to\)B系统\(P'\)点的变换：

\[P'=M_{xyz,x'y'z'}P \]

变换矩阵的推导

上一节根据2D经验，构造出3D情形下坐标系变换对应的旋转矩阵，能否用数学方法推导出该变换呢？

答案是可以，不过要用到解析几何知识. （参见解析几何笔记：空间的正交变换和仿射变换）.

笛卡尔坐标系下，平移、旋转、缩放都是空间的正交变换.

设正交变换\(ψ\)，将直角标架\(Ⅰ[O;\bm{e_1},\bm{e_2},\bm{e_3}]\)变换为\(Ⅱ[O';\bm{e_1'},\bm{e_2'},\bm{e_3'}]\)，其中\(O'(x_0,y_0,z_0)^Ⅰ\). 点的变换是直角标架的逆变换.

有\(Ⅰ[O;\bm{e_1},\bm{e_2},\bm{e_3}]\xrightarrow{ψ}Ⅱ[O';\bm{e_1'},\bm{e_2'},\bm{e_3'}]\)

∴

\[\begin{pmatrix}x'\\y'\\z'\end{pmatrix} =A\begin{pmatrix}x\\y\\z\end{pmatrix}+\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix} \]

将复合变换\(ψ\)分解为旋转变换\(σ\)和平移变换\(τ\)

\[ψ=τσ\\ σ:\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=A_1\begin{pmatrix}x\\y\\z\end{pmatrix}, A_1=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{pmatrix}\\ τ:\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=A_2\begin{pmatrix}x\\y\\z\end{pmatrix}+\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}, A_2=I=\begin{pmatrix}1&&\\&1&\\&&1\end{pmatrix} \]

∵\(Ⅰ[O;\bm{e_1},\bm{e_2},\bm{e_3}]\xrightarrow{ψ=τσ}Ⅱ[O';\bm{e_1'},\bm{e_2'},\bm{e_3'}]\)
∴

\[\begin{cases} \overline{ψ}(\bm{e_1})=\bm{e_1'},\\ \overline{ψ}(\bm{e_2})=\bm{e_2'},\\ \overline{ψ}(\bm{e_3})=\bm{e_3'} \end{cases} \]

∵平移不改变向量大小、方向
∴对于任一向量\(\bm{α}\),\(\overline{ψ}(\bm{α})=\overline{τ}\overline{σ}(\bm{α})=\overline{τ}(\overline{σ}(\bm{α}))=\overline{σ}(\bm{α})\)
∴

\[\begin{cases} \overline{ψ}(\bm{e_1})=\overline{σ}(\bm{e_1})=\bm{e_1'},\\ \overline{ψ}(\bm{e_2})=\overline{σ}(\bm{e_1})=\bm{e_2'},\\ \overline{ψ}(\bm{e_3})=\overline{σ}(\bm{e_1})=\bm{e_3'} \end{cases} \]

∵已知

\[\bm{e_1}=\begin{pmatrix}1\\0\\0\end{pmatrix}, \bm{e_2}=\begin{pmatrix}0\\1\\0\end{pmatrix}, \bm{e_3}=\begin{pmatrix}0\\0\\1\end{pmatrix}\\ \bm{e_1'}=\bm{u}=\begin{pmatrix}u_x\\u_y\\u_z\end{pmatrix}, \bm{e_2'}=\bm{v}=\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}, \bm{e_3'}=\bm{n}=\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix} \]

对于\(\bm{e_1}\to \bm{e_1'}\)，

\[\begin{aligned} \begin{pmatrix}u_x\\u_y\\u_z\end{pmatrix} &= A_2\begin{pmatrix}1\\0\\0\end{pmatrix}\\ \implies u_x &= a_{11}\\ u_y &= a_{21}\\ u_z &= a_{31} \end{aligned} \]

同理，可由\(\bm{e_2}\to \bm{e_2'}, \bm{e_3}\to \bm{e_3'}\)分别得出：

\[v_x=a_{21},v_y=a_{22},v_z=a_{23}\\ n_x=a_{31},n_y=a_{32},n_z=a_{33} \]

∴\(A_2=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{pmatrix} =\begin{pmatrix}u_x&v_x&n_x\\ u_y&v_y&n_y\\ u_z&v_z&n_z\end{pmatrix}\)

于是，

\[ψ:\begin{pmatrix}x'\\y'\\z'\end{pmatrix} =\begin{pmatrix}u_x&v_x&n_x\\ u_y&v_y&n_y\\ u_z&v_z&n_z\end{pmatrix} \begin{pmatrix}x\\y\\z\end{pmatrix}+\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix} \]

写成齐次坐标形式：

\[ψ:\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix} =\begin{pmatrix}u_x&v_x&n_x&x_0\\ u_y&v_y&n_y&y_0\\ u_z&v_z&n_z&z_0\\ 0&0&0&1\end{pmatrix} \begin{pmatrix}x\\y\\z\\1\end{pmatrix} \]

已经求出直角标架的变换，而我们要求的是点的变换，如何求？

∵点的变换是直角标架的逆变换
∴点的变换

\[\begin{pmatrix}x\\y\\z\end{pmatrix}=A^{-1}\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-A^{-1}\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix} \]

∵直角标架的旋转、平移变换是正交变换
∴复合变换也是正交变换
∴\(A\)是正交矩阵
∴\(A^{-1}=A^T=\begin{pmatrix}u_x&u_y&u_z\\ v_x&v_y&v_z\\ n_x&n_y&n_z\end{pmatrix}\)

---

注意：只有正交变换对应的过渡矩阵才是正交矩阵，齐次变换的系数矩阵不一定是正交矩阵.（过渡矩阵参见解析几何笔记：平面的正交变换）

---

∴

\[\begin{aligned} \begin{pmatrix}x\\y\\z\end{pmatrix} &= A^T\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-\begin{pmatrix}u_x&u_y&u_z\\ v_x&v_y&v_z\\ n_x&n_y&n_z\end{pmatrix}\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}\\ &= A^T\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-\begin{pmatrix}u_xx_0 + u_yy_0 + u_zz_0\\ v_xx_0 + v_yy_0 + v_zz_0\\ n_xx_0 + n_yy_0 + n_zz_0\end{pmatrix}\\ &= A^T\begin{pmatrix}x'\\y'\\z'\end{pmatrix}-\begin{pmatrix}\bm{u}\cdot\bm{O'}\\ \bm{v}\cdot \bm{O'}\\ \bm{n}\cdot \bm{O'} \end{pmatrix} \end{aligned} \]

写成齐次坐标形式：

\[\begin{pmatrix}x\\y\\z\\1\end{pmatrix}= \begin{pmatrix}u_x&u_y&u_z&-\bm{u}\cdot\bm{O'}\\ v_x&v_y&v_z&-\bm{v}\cdot \bm{O'}\\ n_x&n_y&n_z&-\bm{n}\cdot \bm{O'}\\ 0&0&0&1\end{pmatrix}\begin{pmatrix}x'\\y'\\z'\\1\end{pmatrix} \]

这就是点\(P(x,y,z)\)从\(A\)系统变换到B系统的变换矩阵：

\[M_{xyz,x'y'z'}=\begin{pmatrix}u_x&u_y&u_z&-\bm{u}\cdot\bm{O'}\\ v_x&v_y&v_z&-\bm{v}\cdot \bm{O'}\\ n_x&n_y&n_z&-\bm{n}\cdot \bm{O'}\\ 0&0&0&1\end{pmatrix} \]

小结

坐标系的转换与对象的转换是反的. i.g. \(x'y'\)轴转换到\(xy\)轴，但该变换对应：将\(xy\)系统的对象转换到\(x'y'\)系统。