三维几何变换,是在二维基础上扩展z坐标得到。三维位置齐次坐标表示为4元列向量。任意三维变换序列,可合并相应变换矩阵,而得到一个复合变换矩阵来表示。
三维平移
点的平移
任意点P=(x,y,z)按向量\((t_x,t_y,t_z)\)平移后,得到新位置\(P'=(x',y',z')\),有:
\[\tag{1}
x'=x+t_x, y'=y+t_y,z'=z+t_z
\]
用4元列向量齐次坐标表示平移变换,变换操作T是4x4矩阵:
\[\tag{2}
\begin{bmatrix}
x' \\
y' \\
z' \\
1
\end{bmatrix}
=\begin{bmatrix}
1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\cdot \begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}
\]
简洁形式:
\[\tag{3}
P'=T\cdot P
\]
对象的平移
对象的平移通过定义该对象的所有点的平移来实现。如果对象用一组多边形表示,这可将各个表面的顶点进行平移。
三维旋转
对象可以绕任意轴旋转,但绕平行于坐标轴的旋转更容易处理,故先讨论。
正旋转方向:视线沿着坐标轴负向观察原点,绕坐标轴逆时针旋转定义为正向旋转。
绕主轴旋转
看作绕z轴的2D旋转,坐标变换:
\[\tag{4}
\begin{aligned}
x' &= x\cos \theta - y\sin \theta \\
y' &= x\sin \theta + y\cos \theta \\
z' &= z
\end{aligned}
\]
变换矩阵:
\[R_z(\theta)=\begin{bmatrix}
\cos\theta & -\sin\theta & 0 & 0\\
\sin\theta & \cos\theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
齐次坐标的矩阵形式:
\[\tag{5}
\begin{bmatrix}
x' \\
y' \\
z' \\
1
\end{bmatrix}
=\begin{bmatrix}
\cos \theta & -\sin \theta & 0 & 0 \\
\sin \theta & \cos \theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\cdot \begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}
\]
其中,\(\theta\)表示绕z轴旋转角度。
简洁形式:
\[\tag{6}
P'=R_z(\theta)\cdot P
\]
基于(4),用y替代x、z替代y、x替代z。循环替换顺序:
\[\tag{7}
x\xrightarrow{}y\xrightarrow{}z\xrightarrow{}x
\]
坐标变换:
\[\tag{8}
\begin{aligned}
y'&=y\cos\theta - z\sin\theta \\
z'&=y\sin\theta + z\cos\theta \\
x'&=x
\end{aligned}
\]
变换矩阵:
\[R_x(\theta)=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & \cos\theta & -\sin\theta & 0\\
0 & \sin\theta & \cos\theta & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
\[\tag{9}
\begin{aligned}
z'&=z\cos\theta-x\sin\theta \\
x'&=z\sin\theta+x\cos\theta \\
y'&=y
\end{aligned}
\]
变换矩阵:
\[R_y(\theta)=\begin{bmatrix}
\cos\theta & 0 & \sin\theta & 0\\
0 & 1 & 0 & 0\\
-\sin\theta & 0 & \cos\theta & 0\\
0 & 0 & 0 &1
\end{bmatrix}
\]
用\(-\theta\)替换旋转角\(\theta\),可得到原旋转的逆。根据(5),
\[\tag{10}
\begin{aligned}
R_z(-\theta)&=\begin{bmatrix}
\cos\theta & \sin\theta & 0 \\
-\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{bmatrix} \\&= R_z(\theta)^T
\end{aligned}
\]
对于绕x、y轴旋转,这种求逆矩阵的方法也适用。
可复合平移、旋转变换得到:
1)平移对象,使旋转轴与平行于该轴的坐标轴重合;
2)绕主轴进行指定旋转;
3)平移对象,将旋转轴移回原来的位置。
假设旋转轴//x轴,那么:
\[\tag{11}
\begin{aligned}
P'&=R(\theta)\cdot P \\
&=T^{-1}\cdot R_x(\theta)\cdot T\cdot P
\end{aligned}
\]
其中,\(R(\theta)\)为绕旋转轴旋转的复合变换矩阵,\(R_x(\theta)\)为绕x轴旋转的变换矩阵,\(\theta\)是旋转角。
绕任意轴旋转
要得到旋转矩阵,有两种方法:
A)复合:复合平移、绕主轴旋转;
B)分解:分解旋转向量到平行、垂直主轴方向。
方法A步骤:
1)平移对象,使旋转轴通过坐标原点;
2)旋转对象,使旋转轴与某一坐标轴重合;
3)绕该坐标轴旋转指定角度;
4)逆旋转,回到原来的方向;
5)逆平移,回到原来的位置。
tips: 比绕平行于主轴的旋转多一步,即先将旋转轴旋转到与坐标轴重合。
假设旋转轴由2个点确定:\(P_1(x_1,y_1,z_1), P_2(x_2,y_2,z_2)\)。沿着P2到P1的方向观察,逆时针为旋转正方向,则旋转轴向量V可定义为:
\[\tag{12}
\begin{aligned}
V&=P_2-P_1 \\
&=(x_2-x_1,y_2-y_1,z_2-z_1)
\end{aligned}
\]
旋转轴的单位向量u:
\[u={V\over |V|}=(a,b,c)
\]
其中,分量a、b、c为旋转轴的方向余弦:
\[\tag{13}
a={x_2-x_1\over |V|}, b={y_2-y_1\over |V|}, c={z_2-z_1\over |V|}
\]
tips:何为方向余弦?
假设u与x、y、z轴夹角分别为\(\alpha, \beta, \gamma\),则:
\[\begin{aligned}
u&=(|u|\cos\alpha, |u|\cos\beta, |u|\cos\gamma)\\
&=(1\cos\alpha, 1\cos\beta, 1\cos\gamma)\\
&=(\cos\alpha, \cos\beta, \cos\gamma)
\end{aligned}
\]
∴u的分量a、b、c称为方向余弦。
如何得到绕任意轴旋转的复合变换矩阵?
对每步分析:
1)平移对象,使旋转轴通过原点。由于需要从P2往P1看的逆时针旋转,因此将P1平移至原点。变换矩阵:
\[\tag{14}
T=\begin{bmatrix}
1 & 0 & 0 & -x_1 \\
0 & 1 & 0 & -y_1 \\
0 & 0 & 1 & -z_1 \\
0 & 0 & 0 & 1
\end{bmatrix}
\]
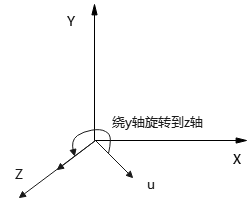
2)将旋转轴u旋转至与z轴重合。分2次:绕x轴旋转到xz平面,绕y轴旋转至与z轴重合。旋转变换需要求出旋转角对应的正弦、余弦值。
u分2步旋转到z轴的示意图(逆时针旋转):
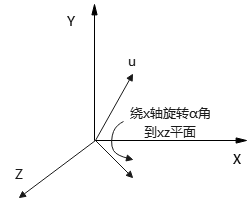
(1)将u绕x轴旋转α角至xz平面得到\(u''\),此时u在yz平面投影\(u'=(0,b,c)\)旋转至z轴.
∵α难以直接求解
∴利用u在yz平面投影\(u'\)求解,此时\(u'\)绕x轴旋转α角与z轴重合:
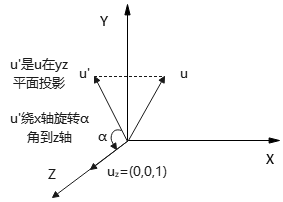
注意:\(u'\)不一定是单位向量,而\(u_z\)是+z轴单位向量.
有:
\[\tag{15}
\cos\alpha={u'\cdot u_z\over |u'||u_z|}={c\over d}
\]
其中,\(u_z\)+z轴单位向量,d为\(u'\)的模。
\[\tag{16}
u_z=(0,0,1), d=|u'|=\sqrt{b^2+c^2}
\]
旋转矩阵:
\[\tag{17}
R_x(\alpha)=\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha & 0 \\
0 & \sin\alpha & \cos\alpha & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\]
而\(\sin\alpha\)可由\(u',u_z\)叉积得到:
\[\begin{aligned}
u'\times u_z&=u_x(|u'||u_z|\sin\alpha)\\
&=u_x|u'|\cdot 1\cdot \sin\alpha \\
&= u_x\cdot b
\end{aligned}
\]
又
\[u_x=(1,0,0)\implies |u_x|=1 \\
\therefore d\sin\alpha=b, \sin\alpha={b\over d} \tag{18}
\]
将\(\cos\alpha, \sin\alpha\)值代入(17),可得:
\[\tag{19}
R_x(\alpha)=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & {c\over d} & -{b\over d} & 0\\
0 & {b\over d} & {c\over d} & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
(2)再绕y轴旋转β角,将u旋转至z轴。
\[u(a,b,c)\xrightarrow{(1)绕x轴旋转α}u''(a,0,d)\xrightarrow{(2)绕y轴旋转β}u_z(0,0,1)
\]
为何\(u''\)的z分量为d?
因为\(u''\)位于xz平面,所以y分量为0。设\(u''=(a,0,z)\),有
\[\begin{aligned}
&\because u''由u旋转得到\\
&\therefore 长度不变, |u''|=\sqrt{a^2+z^2}=|u|=\sqrt {a^2+b^2+c^2} = 1\\
&\therefore |z|=\sqrt{b^2+c^2}\\
&\because |u'|=d=\sqrt{b^2+c^2}\\
&\therefore |z|=d
\end{aligned}
\]
这里取z=d。
思考:为什么z=d,而不是z=-d?
Donald Hearn注,蔡士杰译《计算机图形学(第4版)》解释:因为\(u'\)旋转到z轴上,故\(u''\)的z分量为d。这里不以为意,因为\(u'\)是u在yz平面投影,与\(u''\)并没有直接联系。而且,d为u'的模(正值),但u旋转后得到\(u''\)的z分量完全可能为负值。
点积求\(\cos\beta\):
\[\tag{20}
\cos\beta={u''\cdot u_z\over |u''||u_z|}={(a,0,d)\cdot (0,0,1)\over |1||1|}={d\over 1}=d
\]
叉积求\(\sin\beta\):
\[\begin{aligned}
u''\times u_z&=u_y|u''||u_z|\sin\beta =u_y\cdot (-a)
\end{aligned} \\
\implies \sin\beta=-a \tag{21}
\]
∴\(u''\)绕y轴的旋转矩阵:
\[\tag{22}
R_y(\beta)=\begin{bmatrix}
\cos\beta & 0 & \sin\beta & 0\\
0 & 1 & 0 & 0\\
-\sin\beta & 0 & \cos\beta & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
=\begin{bmatrix}
d & 0 & -a & 0\\
0 & 1 & 0 & 0\\
a & 0 & d & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
3)绕旋转轴旋转
此时,旋转轴与z轴重合,绕z轴旋转\(\theta\)角的变换矩阵:
\[\tag{23}
R_z(\theta)=\begin{bmatrix}
\cos\theta & -\sin\theta & 0 & 0\\
\sin\theta & \cos\theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
4)5)逆旋转、逆平移回原来的方向、位置
对绕任意轴的旋转,复合变换矩阵为:
\[\tag{24}
\begin{aligned}
R(\theta)=&T^{-1}\cdot R_x^{-1}(\alpha)\cdot R_y^{-1}(\beta)\cdot R_z(\theta)\cdot R_y(\beta)\cdot R_x(\alpha)\cdot T\\
=&\begin{bmatrix}
1 & 0 & 0 & x_1 \\
0 & 1 & 0 & y_1 \\
0 & 0 & 1 & z_1 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & {c\over d} & -{b\over d} & 0\\
0 & {b\over d} & {c\over d} & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
d & 0 & a & 0\\
0 & 1 & 0 & 0\\
-a & 0 & d & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\theta & -\sin\theta & 0 & 0\\
\sin\theta & \cos\theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}\\
\cdot &\begin{bmatrix}
d & 0 & -a & 0\\
0 & 1 & 0 & 0\\
a & 0 & d & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & {c\over d} & {b\over d} & 0\\
0 & -{b\over d} & {c\over d} & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -x_1 \\
0 & 1 & 0 & -y_1 \\
0 & 0 & 1 & -z_1 \\
0 & 0 & 0 & 1
\end{bmatrix}
\end{aligned}
\]
将\(R(\theta)\)表示为a,b,c,d,θ的矩阵,而a,b,c,d前面已求得,θ已知.
- 方法B:分解旋转轴向量到平行、垂直方向,然后构造出变换矩阵
该方法无矩阵乘法,直接构造出变换矩阵,因此实际应用中更常用.
设旋转轴单位方向向量\(n(n_x,n_y,n_z)\),绕n旋转θ角的变换矩阵\(R(n,\theta)\). 空间中任一向量\(v\),经旋转变换后得到\(v'\). 有:
\[v'=R(n,\theta)v
\]
tips:v写成列向量形式.
下面求解\(R(n,\theta)\):
将v分解为2个向量\(v_{//},v_{⊥}\),分别平行于n、垂直于n,且\(v=v_{//}+v_{⊥}\)
∵\(v_{//}//n\)
∴绕n旋转不会改变该分量
∴要求\(v'\),只需要求\(v_{⊥}'\)即可
∴\(v'=v_{//}'+v_{⊥}'=v_{//}+v_{⊥}'\)
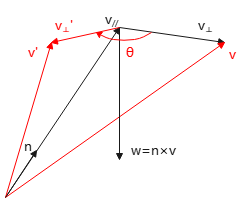
几个向量说明:
\(v_{//}\)是v平行于n的分量,即v在n上的投影\(proj_n{v}\);
\(v_{⊥}\)是v垂直于n的分量,即v在n上的外射影\(perp_n{v}\). \(v=v_{//}+v_{⊥}\implies v_{⊥}=v-v_{//}\);
临时向量w由\(v_{⊥}\)沿-n方向看过去逆时针旋转90°得到,有\(w⊥v_{//},w⊥v_{⊥}\)且\(|w|=|v_{⊥}|\),即\(w=n\times v_{⊥}\)
\[v_{⊥}'=v_{⊥}\cos \theta + w\sin \theta
\]
又
\[\begin{aligned}
v_{//}&=(v\cdot n)n\\
v_{⊥}&=v-v_{//}=v-(v\cdot n)n\\
w&=n\times v_{⊥}\\
&=n\times [v-(v\cdot n)n]\\
&=n\times v-0\\
&=n\times v
\end{aligned}
\]
可得
\[\begin{aligned}
v_{⊥}'&=v_{⊥}\cos \theta + w\sin \theta\\
&=(v-(v\cdot n)n)\cos\theta + (n\times v)\sin \theta\\
\implies v'&=v_{⊥}'+v_{//}'\\
&=v_{⊥}'+v_{//}\\
&=(v-(v\cdot n)n)\cos\theta + (n\times v)\sin \theta+(v\cdot n)n
\end{aligned}
\]
已经得到\(v', v, n, \theta\)的关系,可以通过计算基向量\(p=(1,0,0)^{-1},q=(0,1,0)^{-1},r=(0,0,1)^{-1}\)变换后的向量,从而构造出旋转变换矩阵.
对于第一个向量p
\[\begin{aligned}
p&=\begin{pmatrix}1\\0\\0\end{pmatrix}\\
p'&=R(n,\theta)p\\
&=(p-(p\cdot n)n)\cos\theta+(n\times p)\sin\theta+(p\cdot n)n\\
&=[\begin{pmatrix}1\\0\\0\end{pmatrix}-(\begin{pmatrix}1\\0\\0\end{pmatrix}\cdot \begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix})\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}]\cos\theta + (\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}\times \begin{pmatrix}1\\0\\0\end{pmatrix})\sin\theta+(\begin{pmatrix}1\\0\\0\end{pmatrix}\cdot \begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix})\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}\\
&=[\begin{pmatrix}1\\0\\0\end{pmatrix}-n_x\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}]\cos\theta + \begin{pmatrix}0\\n_z\\-n_y\end{pmatrix}\sin\theta+n_x\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}\\
&=\begin{pmatrix}1-n_x^2\\-n_xn_y\\-n_xn_z\end{pmatrix}\cos\theta + \begin{pmatrix}0\\n_z\sin\theta\\-n_y\sin\theta\end{pmatrix}+\begin{pmatrix}n_x^2\\n_xn_y\\n_xn_z\end{pmatrix}\\
&=\begin{pmatrix}
\cos\theta - n_x^2\cos\theta+n_x^2\\
-n_xn_y\cos\theta+n_z\sin\theta+n_xn_y\\
-n_xn_z\cos\theta-n_y\sin\theta+n_xn_z
\end{pmatrix}\\
&=\begin{pmatrix}
n_x^2(1 - \cos\theta)+ \cos\theta\\
n_xn_y(1 - \cos\theta) + n_z\sin\theta\\
n_xn_z(1-\cos\theta)-n_y\sin\theta
\end{pmatrix}
\end{aligned}
\]
tips: 外积的坐标计算参见解析几何笔记:向量的外积
同理,可得
\[\begin{aligned}
q&=\begin{pmatrix}0\\1\\0\end{pmatrix}\\
q'&=\begin{pmatrix}
n_xn_y(1 - \cos\theta) - n_z\sin\theta\\
n_y^2(1 - \cos\theta) + \cos\theta\\
n_yn_z(1-\cos\theta) + n_x\sin\theta
\end{pmatrix}\\
r&=\begin{pmatrix}0\\0\\1\end{pmatrix}\\
r'&=\begin{pmatrix}
n_xn_z(1 - \cos\theta) + n_y\sin\theta\\
n_yn_z(1 - \cos\theta) - n_x\sin\theta\\
n_z^2(1-\cos\theta) + \cos\theta
\end{pmatrix}
\end{aligned}
\]
根据基向量,构造出\(R(n,\theta)\):
\[\begin{aligned}
\begin{pmatrix}p' & q' & r'\end{pmatrix}&=R\begin{pmatrix}p & q & r\end{pmatrix}=R
\begin{pmatrix}
1 & 0 & 0\\
0&1&0\\
0&0&1\end{pmatrix}=RI=R\\
\implies R(n,\theta)&=\begin{pmatrix}p' & q' & r'\end{pmatrix}\\
&=\begin{pmatrix}
n_x^2(1 - \cos\theta)+ \cos\theta & n_xn_y(1 - \cos\theta) - n_z\sin\theta & n_xn_z(1 - \cos\theta) + n_y\sin\theta\\
n_xn_y(1 - \cos\theta) + n_z\sin\theta & n_y^2(1 - \cos\theta) + \cos\theta & n_yn_z(1 - \cos\theta) - n_x\sin\theta\\
n_xn_z(1-\cos\theta)-n_y\sin\theta & n_yn_z(1-\cos\theta) + n_x\sin\theta & n_z^2(1-\cos\theta) + \cos\theta
\end{pmatrix}
\end{aligned}
\]
三维缩放
相对于原点的缩放
相对于原点的3D缩放变换:
\[\tag{25}
\begin{bmatrix}
x' \\ y' \\ z' \\ 1
\end{bmatrix}
=\begin{bmatrix}
s_x & 0 & 0 & 0\\
0 & s_y & 0 & 0\\
0 & 0 & s_z & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\cdot \begin{bmatrix}
x \\ y \\ z \\ 1
\end{bmatrix}
\]
其中,缩放系数\(s_x, s_y, s_z\)为指定的任意正值。原坐标与变换后坐标关系为:
\[\tag{26}
\begin{aligned}
x'&=x\cdot s_x\\
y'&=y\cdot s_y\\
z'&=z\cdot s_z
\end{aligned}
\]
简写:
\[\tag{27}
P'=S\cdot P
\]
缩放系数>1 ,代表沿该方向放大物体;缩放系数<1,缩小物体;\(s_x=s_y=s_z=1\),代表保持原来的形状。缩放系数必须>0。
相对于任意点的缩放
步骤:
- 平移指定点到原点;
- 相对于原点缩放对象;
- 平移回原位置。
相对于任意点\((x_f,y_f,z_f)\)的缩放变换矩阵:
\[\tag{28}
\begin{aligned}
&T(x_f,y_f,z_f)\cdot S(s_x,s_y,s_z)\cdot T(-x_f, -y_f, -z_f)\\
=&
\begin{bmatrix}
1 & 0 & 0 & x_f\\
0 & 1 & 0 & y_f\\
0 & 0 & 1 & z_f\\
0 & 0 & 0 & 1
\end{bmatrix}
\cdot \begin{bmatrix}
s_x & 0 & 0 & 0\\
0 & s_y & 0 & 0\\
0 & 0 & s_z & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\cdot \begin{bmatrix}
1 & 0 & 0 & -x_f\\
0 & 1 & 0 & -y_f\\
0 & 0 & 1 & -z_f\\
0 & 0 & 0 & 1
\end{bmatrix}\\
=&\begin{bmatrix}
s_x & 0 & 0 & (1-s_x)x_f\\
0 & s_y & 0 & (1-s_y)y_f\\
0 & 0 & s_z & (1-s_z)z_f\\
0 & 0 & 0 & 1
\end{bmatrix}
\end{aligned}
\]
三维复合变换
类似于2D复合变换,可将3D变换序列中各个变换矩阵相乘,得到3D复合变换。最右边的矩阵是最先作用于对象的,最左边的最后起作用。
OpenGL矩阵栈
可用glMatrixMode选择4种模式:建模观察、投影、纹理、颜色。OpenGL为每种模式都维护一个矩阵栈。开始时,每个栈仅包含单位矩阵;处理场景时,栈顶的矩阵称为该模式的“当前矩阵”。在指定观察和几何变换后,建模观察栈(modelview matrix stack)顶是一个4x4复合矩阵,应用于场景的观察变换和各种几何变换。如果要创建多个视图和变换序列,就需要分别保存复合矩阵,所以OpenGL提供深度至少为32的建模观察栈。
glGetIntegerv(GL_MAX_MODELVIEW_STACK_DEPTH, stackSize);
将一个整数值返回给数组stackSize。另外3个矩阵模式(投影、纹理、颜色)的栈深度至少为2,可用下列符号常量确定:GL_MAX_PROJECTION_STACK_DEPTH, GL_MAX_TEXTURE_STACK_DEPTH, GL_MAX_COLOR_STACK_DEPTH。
glGetIntegerv(GL_MODELVIEW_STACK_DEPTH, numMats);
如果在栈处理前调用该函数,则返回1,此时仅包含单位阵。类似的复合常量也可用来确定其他三个栈中当前矩阵数
复制栈顶的当前矩阵,并存入第二个栈位置
glPushMatrix();
破坏栈顶矩阵,使第二个矩阵称为当前矩阵。如果“弹出”栈顶,栈内至少要2个矩阵;否则出错。
glPopMatrix();
思考:矩阵栈顶元素已是当前矩阵,压栈操作会复制一个栈顶当前矩阵,有什么用?
图形处理中,可能需要对当前矩阵进行变换操作,但希望操作完后恢复,而且不会影响处理前的当前矩阵,此时拷贝并压栈操作就很有用。








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步