线段裁剪:Cohen-Sutherland算法
裁剪算法
计算机内部存储的图形数据量通常较大,而屏幕只显示其中一部分,因此需要确定哪些部分在显示区域内,哪些在显示区域外。这个过程称为裁剪(clipping)。
裁剪是二维观察(三维观察)的重要部分,参见计算机图形:二维观察。
点裁剪:只需要判断点与正则矩形边界的位置关系。如果落在裁剪矩形内,保留;如果落在裁剪矩形外,则去掉。
直线段裁剪:需要判断线段与裁剪矩形的位置关系,有多种算法:
1)Cohen-Sutherland算法;
2)梁有栋-Barsky算法;
3)Nicholl-Lee-Nicholl算法;
有的文献会通过对象与观察体的位置,严格区分裁剪(clipping)与剔除(culling). 裁剪,指对象与观察体边界相交;剔除,指对象完全位于观察体外.
Cohen-Sutherland线段裁剪算法
基本思想
裁剪窗口对应的正则矩形区域,按边界将平面划分为9部分,每个部分对应一个区域码。通过为线段端点建立区域码,快速判断端点与裁剪矩形的位置关系。
- 当线段在矩形内部时,全部保留;
- 当线段在矩形外部时,全部裁剪掉;
- 当线段与裁剪矩形相交时,求出交点,并裁剪掉矩形外的部分,保留矩形内的线段。最终得到裁剪后的线段。
tips:正则矩形,是指边界与x轴或y轴平行的矩形。
具体步骤
- 对矩形边界划分空间得到9个部分均进行编码,从而得到9个区域码:
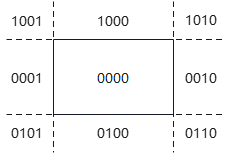
每个区域码用一个4bit二进制数表示,含义:
- 0000 裁剪窗口内部;
- 1001 裁剪窗口左上;
- 0001 裁剪窗口正左侧;
- 0101 裁剪窗口左下;
- 1000 裁剪窗口正上方;
- 0100 裁剪窗口正下方;
- 1010 裁剪窗口右上;
- 0010 裁剪窗口正右侧;
- 0110 裁剪窗口右下。
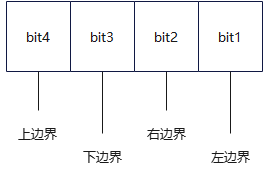
区域码的4个bit位的毎一位都代表一个矩形边界:
- 为线段端点建立区域码
要判断线段与矩形位置关系,先判断端点与矩形的关系,为每个端点建立区域码(含4bit有效区域码)。有2种方法:
方法Ⅰ:比较法
1)如果\(x<xw_{min}\),则bit1 = 1;
2)如果\(x>xw_{max}\),则bit2 = 1;
3)如果\(y<yw_{min}\),则bit3 = 1;
4)如果\(y>yw_{max}\),则bit4 = 1。
方法Ⅱ:取符号位法
1)计算端点坐标与矩形边界的差;
2)用差值设置区域码对应值,bit1为\(x-xw_{min}\)符号位,bit2为\(xw_{max}-x\)符号位,bit3为\(y-yw_{min}\)符号位,bit4为\(yw_{max}-y\)符号位。
- 判断线段与裁剪矩形的位置关系
为线段2端点建立区域码后,就能快速判断与裁剪窗口的位置关系。
1)矩形内:2个端点的区域码进行按位或操作。如果结果为0000,则线段在矩形内,需保留;
2)矩形外:按位与操作。如果有一对相同位置都为1,则线段在矩形外,需丢弃;
3)相交:线段与矩形边界相交,但不一定与矩形相交,需要进一步测试线段与其他边界交点。可能需要多次求交运算完成线段裁剪,每次处理一条边界后,裁掉其中一部分,其余部分对照窗口其余边界进行检查。
- 逐边界对相交线段进行裁剪
假定裁剪矩形边界顺序:左、右、下、上,即bit1->bit4。要检查线段是否与某个裁剪矩形边界相交,可检查2个端点区域码对应bit位:如果一个是1,另一个0,则线段与该边界相交。然而,线段与矩形相交的部分,还需要进一步判断。
下面举例给出具体过程:
如下图,线段\(P_1P_2,P_3P_4\)均与左边界相交,但\(P_1P_2\)与矩形相交,而\(P_3P_4\)在矩形外,

对于线段\(P_1P_2\),端点区域码分别为0100,1001. 按裁剪矩形边界顺序处理(左右下上, bit1->bit3):
1)检查左边界:\(P_1\)在左边界之内,\(P_2\)在之外.
2)计算出与左边界交点\(P_2'\),并裁剪掉左边界之外的部分\(P_2'P_2\).
3)检查右边界:\(P_2',P_1\)均位于右边界之内.
4)检查下边界:\(P_2'\)在下边界之内,\(P_1\)在之外.
5)计算出与下边界交点\(P_1'\),并裁剪掉下边界之外的部分\(P_1'P_1\).
6)检查上边界:\(P_2'\)在上边界之外,\(P_1'\)在之内.
7)计算出与上边界交点\(P_2''\),并裁减掉上边界之外的部分\(P_2'P_2''\).
对于线段\(P_3P_4\),端点区域码分别为0101, 0100. 按矩形边界顺序处理:
1)检查左边界:\(P_3\)在左边界之外,\(P_4\)在内.
2)计算处与左边界交点\(P_3'\),裁剪掉左边界之外的部分\(P_3P_3'\).
3)检查右边界:\(P_3',P_4\)都在左边界之内.
4)检查下边界:\(P_3',P_4\)都在下边界之外,因此都裁剪掉.
- 如何求线段与边界交点?
将边界坐标值(\(x=xw_{min},xw_{max}, y=yw_{min},yw_{max}\)),代入直线点斜式方程:
tips: 斜率不存在时,可单独处理. 或直接采用直线一般方程.
计算分析
对区域进行编码,涉及比较/位运算。
求线段与边界交点时,用到了点斜式,需要先计算直线斜率,涉及到浮点数乘除法运算。因为有4个边界,所以最多需要求4次交点。
程序代码
指定裁剪矩形,对线段裁剪后,绘制线段。
class wcPt2D {
public:
GLfloat x, y;
};
inline GLint round(const GLfloat a)
{
return (GLint)(a + 0.5);
}
// APP窗口尺寸
GLint winWidth = 600, winHeight = 500;
// 边界区域码
const GLint winLeftBitCode = 0x1;
const GLint winRightBitCode = 0x2;
const GLint winBottomBitCode = 0x4;
const GLint winTopBitCode = 0x8;
// 根据区域码判断裁剪点是否位于裁剪矩形内
// 返回值设置成bool 更合适
inline GLint inside(GLint code)
{
return (GLint)(!code);
}
// 判断2个区域码是否位于裁剪矩形外
inline GLint reject(GLint code1, GLint code2)
{
return code1 & code2;
}
// 判断2个区域码是否位于裁剪矩形内
inline GLint accept(GLint code1, GLint code2)
{
return (GLint)!(code1 | code2);
}
// 计算裁剪点pt的区域码
// winMin, winMax包含裁剪区域信息
GLubyte encode(wcPt2D pt, wcPt2D winMin, wcPt2D winMax)
{
GLubyte code = 0x00;
if (pt.x < winMin.x)
code = code | winLeftBitCode;
if (pt.x > winMax.x)
code = code | winRightBitCode;
if (pt.y < winMin.y)
code = code | winBottomBitCode;
if (pt.y > winMax.y)
code = code | winTopBitCode;
return code;
}
void swapPts(wcPt2D* p1, wcPt2D* p2)
{
wcPt2D tmp;
tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void swapCode(GLubyte* c1, GLubyte* c2)
{
GLubyte tmp;
tmp = *c1;
*c1 = *c2;
*c2 = tmp;
}
void lineClipCohSuth(wcPt2D winMin, wcPt2D winMax, wcPt2D p1, wcPt2D p2)
{
GLubyte code1, code2;
GLboolean done = false, plotLine = false;
GLfloat m = 0.0;
while (!done) {
// 为线段2端点建立区域码
code1 = encode(p1, winMin, winMax);
code2 = encode(p2, winMin, winMax);
if (accept(code1, code2)) { // 线段在矩形内
done = true;
plotLine = true;
}
else if (reject(code1, code2)) { // 线段在矩形外
done = true;
}
else { // 线段与矩形相交或在矩形外, 需进一步测试
/* Label the endpoint outside the display window as p1. */
if (inside(code1)) { // 确保在边界外的点是p1, 那么在边界内的是p2
swapPts(&p1, &p2);
swapCode(&code1, &code2);
}
/* Use slope m to find line-clipEdge intersection. */
if (p2.x != p1.x) {
m = (p2.y - p1.y) / (p2.x - p1.x); // 斜率
}
// 按左->右->下->上的顺序, 测试边界是否裁剪后线段相交
if (code1 & winLeftBitCode) { // 与左边界相交, 更新p1到左边界
// 与左边界相交, 则斜率存在
p1.y += (winMin.x - p1.x) * m; // y - y0 = (x - x0)m
p1.x = winMin.x;
}
else if (code1 & winRightBitCode) { // 与右边界相交, 更新p1到右边界
// 与右边界相交, 则斜率存在
p1.y += (winMax.x - p1.x) * m; // y - y0 = (x - x0)m
p1.x = winMax.x;
}
else if (code1 & winBottomBitCode) { // 与下边界相交, 更新p1到下边界
/* Need to update p1.x for nonvertical lines only */
if (p2.x != p1.x) {
p1.x += (winMin.y - p1.y) / m; // x - x0 = (y - y0)/m
}
p1.y = winMin.y;
}
else if (code1 & winTopBitCode) { // 与上边界相交, 更新p1到下边界
if (p2.x != p1.x) {
p1.x += (winMax.y - p1.y) / m; // x - x0 =
(y-y0)/m
}
p1.y = winMax.y;
}
}
}
// 绘制裁剪后的线段p1p2
if (plotLine) {
glBegin(GL_LINES);
glVertex2i(round(p1.x), round(p1.y));
glVertex2i(round(p2.x), round(p2.y));
glEnd();
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号