计算机图形：二维几何变换

目录

• 基本的二维几何变换
  • 二维平移
  • 二维旋转
  • 二维缩放
• 矩阵表示、齐次坐标
  • 齐次坐标
  • 矩阵表示
  • 逆变换
• 复合变换
  • 复合二维平移
  • 复合二维旋转
  • 复合二维缩放
  • 通用二维基准点旋转
  • 通用二维定向缩放
  • 二维刚体变换
• OpenGL几何变换函数
  • 基本OpenGL几何变换
  • OpenGL矩阵操作

基本的二维几何变换

几何变换（geometric transformation）：应用于对象几何描述，并改变其位置、方向、大小的操作。有时，也称为建模变换（modeling transformation）。

常用几何变换函数：平移、旋转、缩放。

二维平移

平移（translation）：点坐标+位移量=>新坐标。平移是只移动对象，而不改变其形状的刚体变换。

二维平移：二维坐标下的平移，即平移距离tx, ty + 原始坐标(x, y) => 新坐标(x', y')，有：

\[\tag{1} x^\prime = x+t_x, y^\prime = y+t_y \]

一对平移距离(tx, ty)称为平移向量（translation vector）或位移向量（shift vector）。

用列向量表示坐标位置、平移向量：

\[\tag{2} P=\begin{bmatrix} x \\ y \end{bmatrix}, P^\prime = \begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix}, T=\begin{bmatrix} t_x \\ t_y \end{bmatrix} \]

平移方程(1)可以用矩阵表示：

\[\tag{3} P^\prime = P + T \]

二维旋转

可指定一个旋转轴（rotation axis）和一个旋转角度（rotation angle）进行一次旋转变换（rotation translation）。

旋转是一种不变形地移动对象的刚体变换。将对象的所有顶点旋转后，对象的所有点就会发生旋转。

对象在xy平面的二维旋转，可看做是绕与z轴平行的旋转轴旋转。记旋转角θ，旋转点(x, y)，对象（三角形）绕选择点旋转如下图所示：

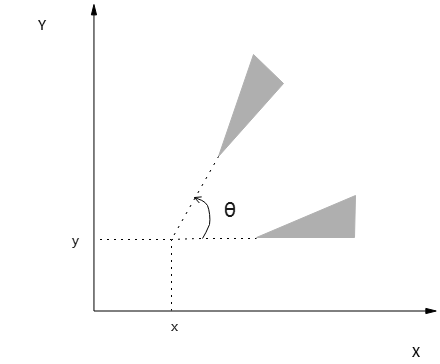
基准点（旋转点）是旋转轴与xy平面交点；正角度θ定义为绕基准点的逆时针旋转，负角度是顺时针旋转。

• 以原点为基准点进行旋转

先确定基准点为原点时，点位置P进行旋转的变换方程。

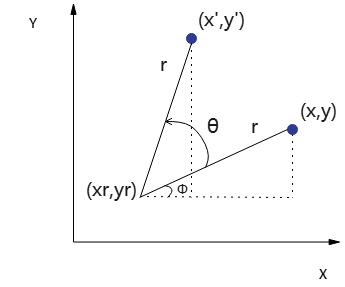
下图是点(x,y)绕原点逆时针旋转角Θ后，得到新位置(x',y')的示意图：

其中，r表示点到原点距离，Φ是点对x轴角位移。

用极坐标表示旋转前点坐标：

\[\tag{4} x=r\cos Φ, y=r\sin Φ \]

旋转后点坐标：

\[\tag{5} \begin{aligned} x^\prime = r\cos (Φ+θ)=r\cos Φ \cos θ - r\sin Φ\sin θ \\ y^\prime = r\sin (Φ+θ) = r\cosΦ \sin θ + r\sin Φ \cos θ \end{aligned} \]

由(4)(5)可得，

\[\tag{6} \begin{aligned} x^\prime = x\cos θ - ysin θ \\ y^\prime = x \sin θ + y \cos θ \end{aligned} \]

用列向量表示坐标位置，那么旋转方程可写成矩阵形式：

\[P^\prime = {R \cdot P} \]

其中，旋转矩阵：

\[R=\begin{bmatrix} \cos θ & -\sin θ \\ \sin θ & \cos θ \end{bmatrix} \]

• 以任意点为基准点进行旋转

点(x,y)绕任意点\((x_r, y_r)\)旋转后，得到新位置\((x^\prime, y^\prime)\)：

\[\tag{7} \begin{aligned} x^\prime = x_r + (x-x_r)\cos θ - (y-y_r)\sin θ \\ y^\prime = y_r + (x-x_r)\sin θ + (y-y_r)\cos θ \end{aligned} \]

点绕任意点旋转示意图：

二维缩放

缩放（scaling）变换改变一个对象的大小。

简单的二维缩放：将缩放系数（scaling factor）\(s_x, s_y\)与对象坐标位置(x,y)相乘。

\[\tag{8} x^\prime = x \cdot s_x, y^\prime = y \cdot s_y \]

缩放系数\(s_x, s_y\)分别表示x方向、y方向对对象缩放。写成矩阵形式：

\[\tag{9} \begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} =\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} \]

\[\tag{10} P^\prime=S\cdot P \]

缩放系数\(s_x, s_y\)可以是任何>0的值。<1 表示缩小，>1表示放大，=1表示不变。当\(s_x, s_y\)相等时，表示一致缩放（uniform scaling）；不相等时，表示差值缩放（differential scaling）。
有些系统也支持<0的缩放系数，表示坐标轴反射。

缩放过程可以选择一个位置不变的点，称为固定点（fixed point），用于控制缩放后对象的位置。固定点\((x_f, y_f)\)可以是对象的中点或其他任何位置。对于顶点(x,y)，缩放后位置\((x^\prime, y^\prime)\)：

\[\tag{11} \begin{aligned} x^\prime - x_f = (x-x_f)s_x, \\ y^\prime - y_f=(y-y_f)s_y \end{aligned} \]

=>

\[\tag{12} \begin{aligned} x^\prime = x\cdot s_x + x_f(1-s_x) \\ y^\prime = y\cdot s_y + y_f(1-s_y) \end{aligned} \]

而\(x_f(1-s_x), y_f(1-s_y)\)对于对象顶点是常数。

固定点\((x_f, y_f)\)，可以将点的缩放写成向量形式：

\[\tag{13} P^\prime = S\cdot P + C \\ S = \begin{bmatrix} s_x & 0 \\ 0 & s_y \\ \end{bmatrix}, P=\begin{bmatrix} x \\ y \end{bmatrix}, C=\begin{bmatrix} x_f(1-s_x) \\ y_f(1-s_y) \end{bmatrix} \]

---

矩阵表示、齐次坐标

综合旋转变换、放缩变换，式(13)可写成：

\[\tag{14} P^\prime = M_1\cdot P + M_2 \]

\(P^\prime, P\)表示列向量(2x1矩阵)，分别表示变换后坐标、变换前坐标；\(M_1\)是包含乘法系数2x2的矩阵，包含旋转或放缩系数；\(M_2\)是2x1列向量，包含平移参数。

变换操作能不能写成矩阵乘法的形式（去掉加法）？
答案是可以，这就需要用齐次坐标。

齐次坐标

齐次坐标（homogeneous coordinate）定义是将一个原本n维的向量用n+1维向量表示。

如果将式(14)中2x2矩阵扩充为3x3，就能把2维几何变换的乘法、平移项组合成单一矩阵表示。
2维位置\((x,y)=>(x_h,y_h,h)\)，我们称后者（3维）是前者（2维）的齐次坐标，齐次参数（homogeneous parameter）h是一个非零值。有

\[\tag{15} x={x_h\over h}, y={y_h\over h} \]

h可以是任意非零值，通常取1。这样，二维齐次坐标可写为：\((x,y,1)^{-1}\)

接下来用齐次坐标改写二维平移、旋转、缩放变换。

矩阵表示

• 二维平移矩阵

\[\tag{16} \begin{bmatrix} x^\prime \\ y^\prime \\ 1 \end{bmatrix} =\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

简写：

\[\tag{17} P^\prime = T(t_x, t_y)\cdot P \]

3x3矩阵\(T(t_x,t_y)\)：平移矩阵，简称T。

• 二维旋转矩阵

以原点为旋转点的二维旋转：

\[\tag{18} \begin{bmatrix} x^\prime \\ y^\prime \\ 1 \end{bmatrix} =\begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

简写：

\[\tag{19} P^\prime = R(\theta) \cdot P \]

3x3矩阵\(R(\theta)\)：旋转矩阵，简称R。

• 二维缩放矩阵

以原点为固定点的二维缩放：

\[\tag{20} \begin{bmatrix} x^\prime \\ y^\prime \\ 1 \end{bmatrix} =\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

简写：

\[\tag{21} P^\prime=S(s_x,s_y)\cdot P \]

3x3矩阵\(S(s_x,s_y)\)：缩放矩阵，简称S。

---

逆变换

如果想通过变换后坐标得到变换前的坐标，就需要用到逆变换。逆矩阵的特点：与原矩阵相成，得到单位矩阵。

• 逆平移矩阵

\[\tag{22} T^{-1}=\begin{bmatrix} 1 & 0 & -t_x \\ 0 & 1 & -t_y \\ 0 & 0 & 1 \end{bmatrix} \]

• 逆旋转矩阵

\[\tag{23} R^{-1}=\begin{bmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

• 逆缩放矩阵

\[\tag{24} S^{-1}=\begin{bmatrix} {1\over s_x} & 0 & 0 \\ 0 & {1\over s_y} & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

---

复合变换

可将任意的变换序列组成复合变换矩阵（composite transformation matrix），用矩阵乘积表示。而变换矩阵的乘积，称为矩阵的合并（concatenation）或复合（composition）。
比如，将位置相同的点进行多次变换，用矩阵乘法的结合律和合并成一个：

\[\tag{25} \begin{aligned} P^\prime &= M_2\cdot M_1\cdot P \\ &= M\cdot P \end{aligned} \]

复合二维平移

结论：2个连续平移是相加的。
证明：
假设2个连续的平移向量\((t_{1x}, t_{1y}), (t_{2x}, t_{2y})\)用于坐标位置P，那么变换位置\(P^\prime\)：

\[\tag{26} \begin{aligned} P^\prime &= T(t_{2x}, t_{2y})\cdot \{T(t_{1x},t_{1y})\cdot P\} \\ &= \{T(t_{2x},t_{2y})\cdot T(t_{1x}, t_{1y})\}\cdot P \end{aligned} \]

\(P, P^\prime\)为三元素、齐次坐标的列向量。

复合平移矩阵：

\[\tag{27} \begin{aligned} T(t_{2x},t_{2y})\cdot T(t_{1x}, t_{1y}) =T(t_{1x}+t_{2x}, t_{1y}+t_{2y}) \\ <=> \begin{bmatrix} 1 & 0 & t_{2x} \\ 0 & 1 & t_{2y} \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & t_{1x} \\ 0 & 1 & t_{1y} \\ 0 & 0 & 1 \end{bmatrix} =\begin{bmatrix} 1 & 0 & t_{1x}+t_{2x} \\ 0 & 1 & t_{1y}+t_{2y} \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

复合二维旋转

结论：2个连续旋转是相加的。
证明：
假设2个连续旋转角度\(θ_1, θ_2\)（逆时针），则位置P变换方程为：

\[\tag{28} \begin{aligned} P^\prime &= R(\theta_2)\cdot \{ R(\theta_1) \cdot P \} \\ &= \{ R(\theta_2)\cdot R(\theta_1)\} \cdot P \end{aligned} \]

复合旋转矩阵：

\[\begin{aligned} R(\theta_2)\cdot R(\theta_1) &= R(\theta_1+\theta_2) \\ <=> \begin{bmatrix} \cos \theta_2 & -\sin \theta_2 & 0 \\ \sin \theta_2 & \cos \theta_2 & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos \theta_1 & -\sin \theta_1 & 0 \\ \sin \theta_1 & \cos \theta_1 & 0 \\ 0 & 0 & 1 \end{bmatrix} &=\begin{bmatrix} \cos (\theta_2+\theta_1) & -\sin (\theta_2 + \theta_1 ) & 0 \\ \sin (\theta_2 +\theta_1) & \cos (\theta_2 + \theta_1) & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

复合二维缩放

结论：2个连续缩放是相乘的。
证明：

\[\tag{29} \begin{aligned} S(s_{2x}, s_{2y})\cdot S(s_{1x},s_{1y}) &= S(s_{1x}\cdot s_{2x}, s_{1y}\cdot s_{2y}) \\ <=> \begin{bmatrix} s_{2x} & 0 & 0 \\ 0 & s_{2y} & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} s_{1x} & 0 & 0 \\ 0 & s_{1y} & 0 \\ 0 & 0 & 1 \end{bmatrix} &= \begin{bmatrix} s_{1x}\cdot s_{2x} & 0 & 0 \\ 0 & s_{1y}\cdot s_{2y} & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

通用二维基准点旋转

有的图形软件包只提供绕坐标原点的旋转函数，我们可通过平移-旋转-平移操作，实现绕任意基准点\((x_r,y_r)\)旋转。步骤如下：

1. 平移对象，让基准点移动到坐标原点；
2. 绕坐标原点旋转；
3. 平移对象，使基准点回原来的位置。

用如下变换矩阵表示：

\[\tag{30} \begin{aligned} T(x_r, y_r)\cdot R(\theta)\cdot T(-x_r,-y_r) &= R(x_r,y_r,\theta) \\ => \begin{bmatrix} 1 & 0 & x_r \\ 0 & 1 & y_r \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -x_r \\ 0 & 1 & -y_r \\ 0 & 0 & 1 \end{bmatrix} &=\begin{bmatrix} \cos \theta & -\sin \theta & x_r(1-\cos \theta)+y_r\sin \theta \\ \sin \theta & \cos \theta & y_r(1-\cos \theta)-x_r\sin \theta \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

通用二维定向缩放

\((s_x,s_y)\)是沿着x、y方向缩放对象。如果想沿着其他方向缩放对象，如何进行？
可以先将缩放方向旋转到坐标轴，然后缩放，最后旋转回原来的方向。
设\(s_1, s_2\)是与坐标轴成θ角的2个垂直方向，定向缩放的复合矩阵：

\[\tag{31} R^{-1}(\theta)\cdot S(s_1,s_2)\cdot R(\theta)=\begin{bmatrix} s_1\cos^2 \theta + s_2\sin^2 \theta & (s_2-s_1)\cos \theta \sin \theta & 0 \\ (s_2-s_1)\cos \theta \sin \theta & s_1\sin^2 \theta+s_2\cos^2 \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

二维刚体变换

如果一个变换矩阵只包含平移、旋转，则为刚体变换矩阵（rigid-body transformation matrix）。一般形式：

\[\tag{32} \begin{bmatrix} r_{xx} & r_{xy} & tr_x \\ r_{yx} & r_{yy} & tr_y \\ 0 & 0 & 1 \end{bmatrix} \]

其中，4个\(r_{jk}\)是多重旋转项，\(tr_x, tr_y\)是平移项。

坐标位置的刚体变化，也称刚体运动（rigid-motion）变换。变换后，坐标位置间所有角度和距离都不变。矩阵(32)左上角2x2矩阵是一个正交矩阵（若\(AA^T=A^TA=E\)，则A为正交矩阵），有：

\[\tag{33} r_{xx}^2+r_{xy}^2=r_{yx}^2+r_{yy}^2=1 \\ r_{xx}r_{xy}+r_{yx}r_{yy}=0 \]

说明2个行向量\((r_{xx}, r_{xy}), (r_{yx}, r_{yy})\)是单位正交向量组（模为1，相互垂直，点积为0）。

可以这将2个正交向量组旋转到x、y轴位置（列向量形式）：

1. 将\((r_{xx},r_{xy})\)旋转到x轴

\[\tag{34} \begin{bmatrix} r_{xx} & r_{xy} & 0 \\ r_{yx} & r_{yy} & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} r_{xx} \\ r_{xy} \\ 1 \end{bmatrix} =\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} \]

2. 将\((r_{yx}, r_{yy})\)旋转到y轴

\[\tag{35} \begin{bmatrix} r_{xx} & r_{yy} & 0 \\ r_{yx} & r_{yx} & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} r_{yx} \\ r_{yy} \\ 1 \end{bmatrix} =\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} \]

例如，将对象进行刚体变换：对于基准点(xr, yr)旋转θ角，然后平移。复合变换矩阵：

\[\tag{36} \begin{aligned} T(t_x,t_y)\cdot R(x_r,y_r,\theta) &= T(t_x,t_y)\cdot \{T(x_r,y_r,\theta)\cdot R(0,0,\theta)\cdot T(-x_r,-x_y)\} \\ &= \begin{bmatrix} \cos \theta & -\sin \theta & x_r(1-\cos \theta) + y_r\sin \theta + t_x \\ \sin \theta & \cos \theta & y_r(1-\cos \theta) - x_r\sin \theta + t_y \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

---

OpenGL几何变换函数

OpenGL实现的几何变换函数，默认适用于3维变换（4x4矩阵），2维空间可固定z值（如z=0）。

基本OpenGL几何变换

OpenGL内部使用复合矩阵支持变换，从而导致变换可累积。

• 生成4x4平移矩阵

// *表示后缀码, 包含数据类型信息, e.g. f-float, d-double
glTranslate*(tx, ty, tz);

调用该函数后，可用于对之后定义的对象位置进行平移变换。

// 将随后定义的对象坐标x方向平移25个单位，y方向平移-10个单位
glTranslaterf(25.0, -10.0, 0.0);

• 生成4x4旋转矩阵

// 向量(vx,vy,vz)是旋转的基准方向
// theta 是逆时针旋转角度, 单位: 度
glRotate*(theta, vx, vy, vz);

• 生成4x4缩放矩阵

// sx, sy, sz为xyz轴方向缩放系数
glScale*(sx, sy, sz);

缩放系数为0会引起错误。

OpenGL矩阵操作

• 设定模式

glMatrixMode(GL_PROJECTION)设定投影模式（projection mode），指定将用于投影变换的矩阵。变换确定怎样将一个场景投影到屏幕上。

glMatrixMode(GL_MODELVIEW)设定几何变换矩阵，此时将该矩阵看做建模观察矩阵（modelview matrix），用于存储和组合几何变换，几何变换与向观察坐标系的变换组合。该语句指定一个4x4建模观察矩阵为当前矩阵（current matrix）。在进行几何变换前，调用该语句。GL_MODELVIEW是默认参数。

glMatrixMode还支持2个模式：

1. 纹理模式（texture mode），用于映射表面的纹理图案；
2. 颜色模式（color mode），用于从一个颜色模型转换到另一个。

• 初始化当前矩阵为单位阵

当前矩阵在进行计算前，需要进行初始化，通常赋值为单位矩阵（Identity Matrix）：

glLoadIdentity();

也可以赋值为其他值：

// 后缀码常用f, d
// elements16 指定一个单下标、16元素的浮点数组
glLoadMatrix*(elements16);

e.g. 下面程序将初始化建模观察模式下的当前矩阵为指定数组elems值：

glMatrixMode(GL_MODELVIEW);

GLfloat elems[16];
GLint k;

for (k = 0; k < 16; k++) {
    elems[k]  = (float)(k);
}
glLoadMatrixf(elems);

结果：

M=[
0.0 4.0   8.0 12.0
1.0 5.0   9.0 13.0
2.0 6.0 10.0 14.0
3.0 7.0 11.0 15.0
]

• 矩阵乘法

将指定矩阵与当前矩阵进行矩阵乘法：

// 后缀码常用f,d
// otherElements16 16元素、单下标数组(一维数组)
glMultMatrix*(otherElements16);

用法：

glMatrixMode(GL_MODELVIEW);

glLoadIdentity(); // 当前矩阵M为单位阵4x4 E
glMultMatrixf(elemsM2); // M = E*M2
glMultMatrixf(elemsM1); // M = M*M1