Bresenham算法画圆
问题背景
如何在屏幕上绘制一个圆?
可以先看看圆的特性,根据其特性决定如何绘制。。
- 圆的特性
圆定义:所有距离中心位置(xc, yc)为给定值r的点集。
圆的方程:
- 根据圆的方程绘制圆
若沿着x轴从\([x_c-r, x_c+r]\)以1为单位步长,计算y值,就能得到圆周每个点位置:
这种方法优点:简单,直观。
缺点:
1)计算量大,每一步都要进行平方、开方运算。
2)所画像素位置的间距不一致,因为x虽然逐像素递增,但y经过平方、开方运算后,并不会随x逐次变化。
- 利用对称性优化圆方程绘制圆
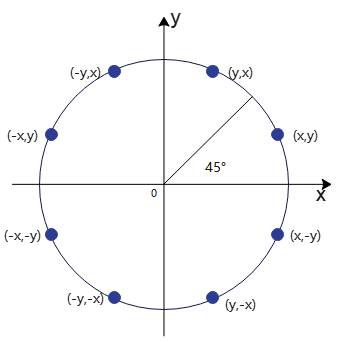
不论用何种算法计算圆周的坐标值(x,y),只需要考虑[0, 45°]的圆周,其他部分圆周可以利用圆的对称性求出。
假设P(x, y)为第一象限圆心角为[0, 45°]的圆周上任意一点,那么可以根据对称性求出另外7点坐标。当P遍历圆弧上每一点时,也就能得到另外7段圆弧。
Bresenham算法画圆
算法推演
如何解决根据圆方程计算像素点位置,而导致的运算量大、像素间距不一致的问题?
可以用Bresenham算法。Bresenham画圆算法,也叫中心点画圆算法。
类似于光栅画线的算法,在每一步以1像素间隔为单位进行取样,确定距离圆周最近的像素点位置。
对于半径r、圆心坐标(xc,yc)点圆,可以先讨论圆心在原点(0,0)的圆,然后将其移动到(xc, yc)。
由圆的对称性可知,只用求第一象限中圆心角为45°的圆弧(1/8圆),此时,圆心与圆上一点连线斜率为0~1。
定义圆函数:
对于任意一点(x,y):
假设当前绘制了像素点\((x_k, y_k)\),那么下一个点\((x_{k+1}, y_{k+1})\)在哪?
有2个选择:\((x_k+1, y_k) or (x_k+1, y_k-1)\)
tips:在第一象限内,圆周点随着x增大y减小(非递增)。
Bresenham的基本思想,是判断哪个点到曲线的距离更近,就选择那个点。然而,直接求点到圆周的距离会非常复杂,可以通过判断2个备选点的中点\((x_k+1, y_k-1/2)\)与圆的位置关系:
- 当中点位于圆内时,则\(y_k\)更接近圆;
- 当中点位于圆外时,则\(y_k-1\)更接近圆;
tips:一个最简单的理解方式,就是考虑极端情况,如\(y_k\)在圆上(最接近),则中点肯定在圆内;\(y_k-1\)在圆上(最接近),则中点肯定在圆外。
于是,决策参数:
当k取值k+1时,有
当\(p_k < 0\)时,中点位于圆内,\(y_k\)更接近圆;
当\(p_k > 0\)时,中点位于圆外,\(y_k-1\)更接近圆;
做差值,有
因为,\(x_{k+1}=x_k+1\)且,
对于初值\(p_0\),在起始点\((x_0,y_0)=(0, r)\)处求值即可:
如果半径r为整数,则可以对\(p_0\)取整:\(p_0=1-r\)
算法步骤
Bresenham算法画圆步骤,可以归纳如下:
- 输入圆半径r, 圆心\((x_c, y_c)\),得到圆周(圆心移动到原点)上第一个点:\((x_0,y_0)=(0,r)\);
- 计算决策参数的初值:\(p_0=5/4-r\);
- 从k=0开始,对每个\(x_k\)进行以下计算及判断:
如果\(p_k<0\),则圆的下一个点为\((x_{k+1}, y_k)\),且\(p_{k+1}=p_k+2x_{k+1}+1\)
如果\(p_k>0\),则圆的下一个点为\((x_{k+1}, y_k-1))\),且\(p_{k+1}=p_k+2x_{k+1}+1-2y_{k+1}\) - 计算得到1/8后,可用对称性得到其他7个部分;
- 将计算出的像素位置(x,y)移回圆心\((x_c,y_c)\)的圆周上,并绘制出像素点:
- 重复3~5,直至x≥y。
算法程序
Bresenham算法画圆程序如下。
注意:算法求出1/8圆弧的像素点,然后用对称性得到另外7/8的像素点。
// 在指定坐标(xCoord,yCoord)绘制像素点
void set_pixel(GLint xCoord, GLint yCoord)
{
glBegin(GL_POINTS);
glVertex2i(xCoord, yCoord);
glEnd();
}
// 绘制圆心(xc,yc), 半径radius的圆
void circleMidpoint(GLint xc, GLint yc, GLint radius)
{
screenPt circPt; // 圆周上的点(像素点)
GLint p = 1 - radius; // Initial value for midpoint parameter
circPt.setCoords(0, radius); // Set coordinates for top point of circle.
circlePlotPoints(xc, yc, circPt);
while (circPt.getx() < circPt.gety()) {
circPt.incrementx();
if (p < 0) {
p += 2 * circPt.getx() + 1;
}
else {
circPt.decrementy();
p += 2 * (circPt.getx() - circPt.gety()) + 1;
}
circlePlotPoints(xc, yc, circPt);
}
}
// 用对称性由1/8圆弧的点得到另外7/8圆弧的点, 并绘制出圆周上的点
// (xc, yc) 圆心位置
// circPt 圆心为(0,0)的圆心角0~45°的圆周上点的位置
void circlePlotPoints(GLint xc, GLint yc, screenPt circPt)
{
set_pixel(xc + circPt.getx(), yc + circPt.gety());
set_pixel(xc - circPt.getx(), yc + circPt.gety());
set_pixel(xc + circPt.getx(), yc - circPt.gety());
set_pixel(xc - circPt.getx(), yc - circPt.gety());
set_pixel(xc + circPt.gety(), yc + circPt.getx());
set_pixel(xc - circPt.gety(), yc + circPt.getx());
set_pixel(xc + circPt.gety(), yc - circPt.getx());
set_pixel(xc - circPt.gety(), yc - circPt.getx());
}
参考
[1]DonaldHearn,M.PaulineBaker,赫恩,等.计算机图形学(第四版)[M].电子工业出版社,2014.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号