算法笔记:并查集
并查集原理
如果某个部落过于庞大,则部落成员见面可能不认识。已知某个部落成员关系图,任意给出其中两个人,判断是否有亲戚关系。规定:1)若x、y是亲戚,y和z是亲戚,则x和z也是亲戚;2)若x、y是亲戚,则x的亲戚也是y的亲戚,y的亲戚也是x的亲戚。
如何才能快速判断2个人是否有亲戚关系?
以上第1)条是传递关系,第2)条相当于两个集合的合并。对该问题可以采用并查集解决。并查集是一种树形数据结构,用于处理集合的合并及查询问题。
算法步骤
(1)初始化。将每个节点所在的集合号都初始化为其自身编号。
(2)查找。查找两个元素所在的集合,即找祖宗。查找时,采用递归的方法找其祖宗,找到祖宗(集合号等于自身)时停止;然后回归,回归时将祖宗到当前节点路径上的所有节点都统一为祖宗的集合号。
(3)合并。若两个节点的集合号不同,则将两个节点合并为一个集合,合并时只需要将一个节点的祖宗集合号修改为另一个节点的祖宗集合号。只需要修改祖宗号即可。
示例图解
假设现在有7个人,首先输入亲戚关系图,然后判断两个人是否有亲戚关系。
(1)初始化。
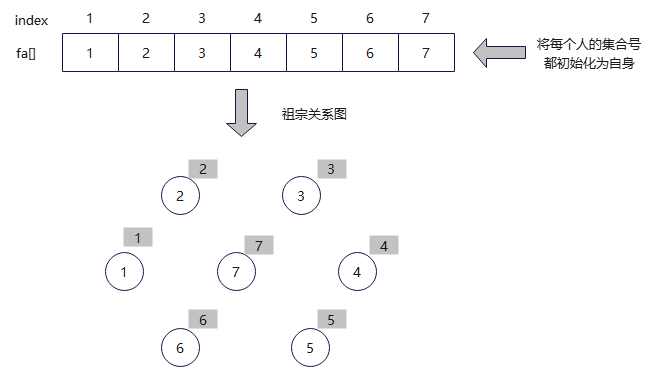
(2)查找。输入亲戚关系2、7,查找到2的集合号为2,7的集合号为7。
(3)合并。两个元素的集合号不同,将两个元素合并为一个集合。在此约定,将小的集合号赋值给大的集合号,也就是将7的集合号修改为2,即fa[7]=2。
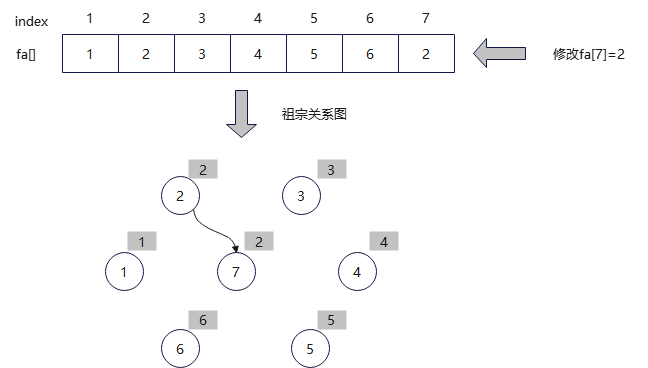
(4)查找。输入亲戚关系4、5,查找到4的集合号4,5的集合号5.
(5)合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[5]=4。
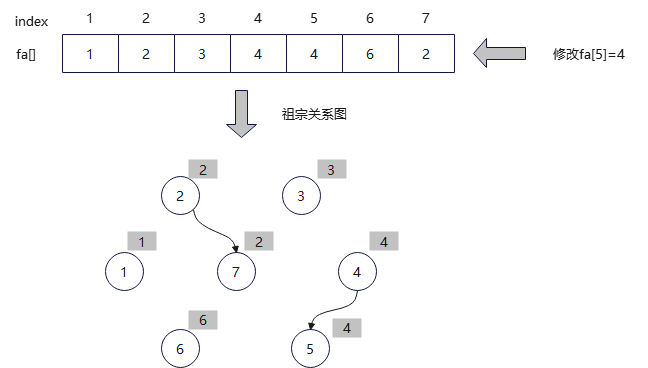
(6)查找。输入亲戚关系3、7,查找到3的集合号3,7的集合号2。
(7)合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[3]=2。
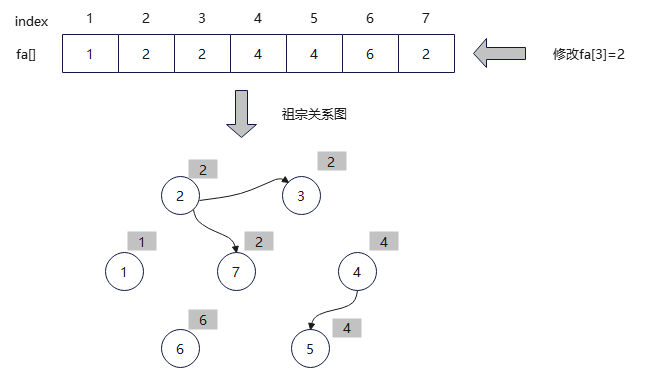
(8)查找。输入亲戚关系4、7,查找到4的集合号为4,7的集合号为2.
(9)合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[4]=2。虽然有2个节点的集合号为4,但只需要修改两个节点中的祖宗,无须将集合号为4的所有节点都检索一遍,而4是节点4、5的祖宗,因此只用修改4的集合号即可。这是并查集的巧妙之处。
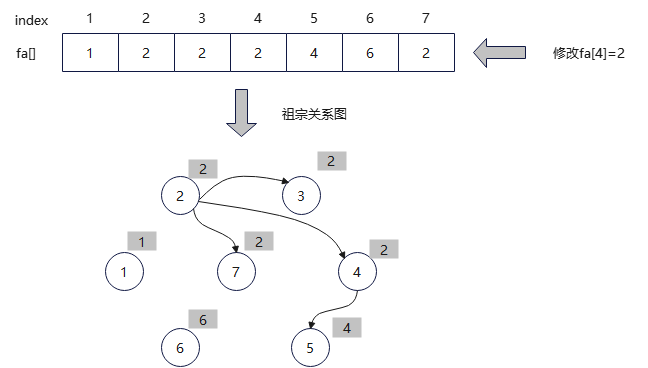
(10)查找。输入亲戚关系3、4,查找到3的集合号2,4的集合号2.
(11)合并。两个元素的集合号相同,无需合并。
(12)查找。输入亲戚关系5、 7,查找到7的集合号2,5的集合号4(不等于5),所有找5的祖宗。首先找到父节点4,4的父节点2,2的集合号2(祖宗),搜索停止。返回时,将祖宗到当前节点路径上所有节点的集合号都统一为祖宗的集合号。更新5的集合号为祖宗的集合号2。修改fa[5]=2.
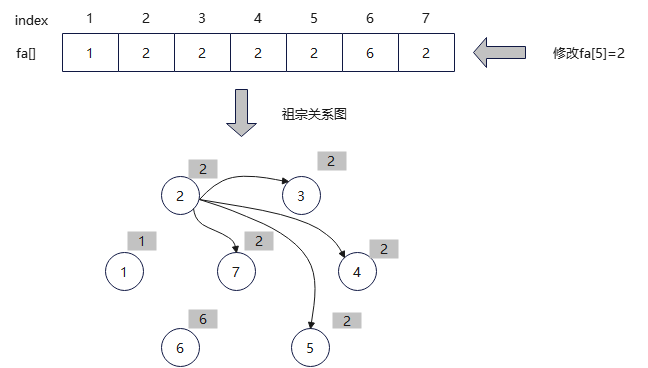
(13)合并。两个元素的集合号相同,无需合并。
(14)查找。输入亲戚关系5、 6,查找到5集合号2,6集合号6.
(15)合并。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[6]=2.
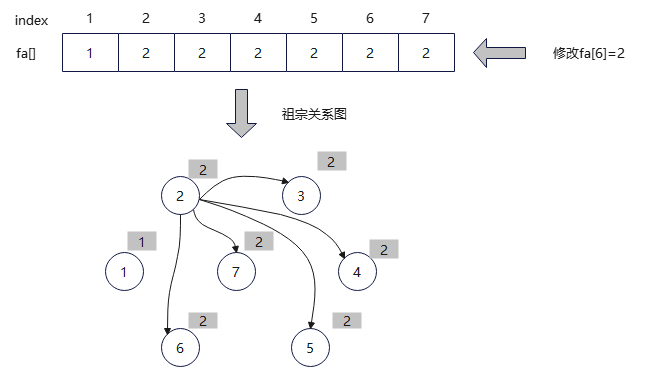
(16)查找。输入亲戚关系2、 3,查找到2的集合号2,3的集合号2.
(17)合并。两个元素的集合号相同,无需合并。
(18)查找。输入亲戚关系1,2,查找到1的集合号1,2的集合号2。两个元素的集合号不同,将两个元素合并为一个集合,修改fa[2]=1。
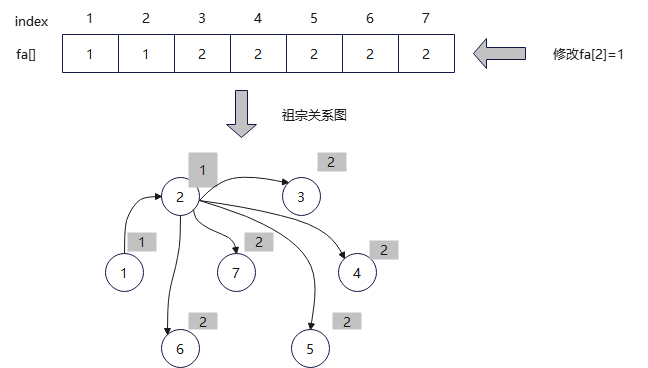
假设导致为止,不再输入亲戚关系。可以看到3/4/5/6/7 这些节点的集合号还没被修改为1,这样做是否可行?
如果要判断5和2是不是亲戚关系,如何进行?
过程:
1)查找到5的集合号2,不等于5,找其祖宗。首先找到5的父节点2,2的父节点1,1的集合号为1(祖宗),搜索停止。将祖宗1到5这条路径上所有节点的集合号都更新为1。
2)查找到2的集合号1,不等于2,找其祖宗。首先找到2的父节点1,1的集合号为1(祖宗),搜索停止。将祖宗1到2这条路上的所有节点的集合号都更新为1.
3)5,2的集合号都是1,因此5和2是亲戚关系。
类似地,也可以判断1与3/4/5/6/7 都是亲戚关系。
算法实现
(1)初始化。将节点i的集合号初始化为其自身编号。
用数组元素fa[i]表示节点i的集合号。fa[i]其实也表示i的父节点。
void init() { // 初始化所有节点集合号
for (int i = 1; i <= n; ++i)
fa[i] = i; // 把节点i的集合号初始化为自身编号
}
(2)查找。查找两个元素所在的集合,即找祖宗。查找的时候,采用递归方法找祖宗(集合号等于自身)。回归时,将祖宗到当前节点路径上所有节点都统一为祖宗的集合号。
只有fa[x] == x,才表示x的祖宗就是自己,搜索停止。否则,要继续向上查找。
// 找节点x的祖宗,递归版本
int Find(int x) {// 查找
if (x!=fa[x]) { // x不是祖宗
fa[x] = Find(fa[x]);
}
return fa[x];
}
// 找节点x的祖宗,循环版本
int Find_2(int x) {
while (x != fa[x]) {
fa[x] = fa[fa[x]];
x = fa[x];
}
return x;
}
(3)合并。先找到x的集合号a,y的集合号b,若a和b相等,则无需合并。若a和b不相等,则将a的集合号修改为b,或者将b的集合号修改为a。只需要修改祖宗即可。
void Union(int x, int y ) {//合并
int a = Find(x);
int b = Find(b);
if (a != b) {
fa[b] = a;
}
}
时间复杂度、空间复杂度
证明参见:Disjoint-set data structure | Wiki
如有n个节点,m次Find或Union操作,那么时间复杂度为O(m logn),其中logn 表示为:
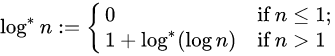
空间复杂度:用到数组用于存储节点集合号,O(n)
实战:LeetCode 547. 省份数量
https://leetcode.cn/problems/number-of-provinces/
https://leetcode.cn/problems/bLyHh0/
题目描述:
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
解析:
这是一个典型的并查集问题,利用vector
// 并查集 求连通分量
int findCircleNum(vector<vector<int>>& isConnected) {
if (isConnected.empty() || isConnected[0].empty()) return 0;
int ans = 0;
vector<int> fa;
fa.resize(isConnected.size() + 1);
// init
for (int i = 1; i < fa.size(); ++i) {
fa[i] = i;
}
// 输入边, 合并集合
for (int i = 0; i < isConnected.size(); ++i) {
for (int j = i + 1; j < isConnected[i].size(); ++j) {
int x, y;
if (isConnected[i][j]) {
x = i + 1; y = j + 1;
Union(fa, x, y);
}
}
}
for (int i = 1; i < fa.size(); ++i) {
if (fa[i] == i) {
ans++;
}
}
return ans;
}
void Union(vector<int>& fa, int x, int y) {
int a = Find(fa, x);
int b = Find(fa, y);
if (a != b) {
fa[a] = b;
}
}
int Find(vector<int>& fa, int x) {
if (x != fa[x]) {
fa[x] = Find(fa, fa[x]);
}
return fa[x];
}
参考
[1]陈小玉.著.算法训练营:海量图解+竞赛刷题(进阶篇)
[2]https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Time_complexity
[3]https://blog.csdn.net/yuzhiqiang666/article/details/80721436


 浙公网安备 33010602011771号
浙公网安备 33010602011771号