SGI STL堆heap
heap简介
heap不是STL容器组件,而是为了辅助priority queue(优先队列)。priority queue允许用户以任何次序将任何元素推入容器内,但取出时一定是从优先权最高(即数值最大)的元素开始取。二叉最大堆(binary max heap)正具有这样的特性,适合作为priority queue的底层实现机制。
可以用数组用来存放二叉堆(binary heap),而binary heap其实也是一种完全二叉树(complate binary tree)。除了最底层叶子节点外,其余地方都是填满的。如下图所示,是一个二叉最大堆:
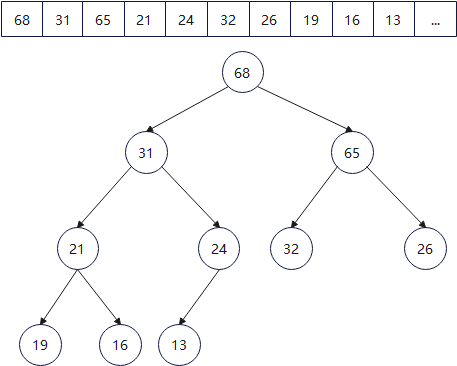
其中,节点i(从数组索引0开始计算)的左儿子位于数组的2i + 1位置,右儿子位于数组的2i + 2的位置。相对地,如果节点位置j,那么父节点位置(j-1)/2。这种用数组来表示tree方式,称为隐式表述法(implicit representation)。
如此,要实现heap,只需要一个数组和一组heap算法,用来插入元素、删除元素、取极值,同时维持heap特性。由于heap插入数据后,可能需要数组动态改变大小,因此选用vector,而不选用固定大小的array。
heap特性
heap分为max heap(最大堆),min heap(最小堆)。
最大堆:任意节点key值不小于左、右儿子的key值。也就是说,最大key值位于根节点。
最小堆:任意节点key值不大于左、右儿子的key值。也就是说,最小key值位于根节点。
不论是建堆,还是插入元素、删除元素,都必须维持堆的特性。
下面的heap算法,都以max heap为例,min heap的算法类似。
heap算法
push_heap 算法
当heap插入一个数据后,该如何保持max-heap特性?
这就是push_heap算法要做的事情。
下图所示,是push_heap算法的实际演练过程。新加入元素要放在树最下面一层的叶子节点,并且填补vector从左到右的第一个空格。也就是说,新插入节点是放在vector的末尾(end())。
插入新元素50,为了维护大堆特性,会由新插入节点的父节点开始上溯,保持父节点key值永远不小于儿子节点key值。如果违反这个特性,就要交换父节点、子节点位置。如此,直到不需要交换节点为止(因为其他节点结构没动,大小关系不会改变)。
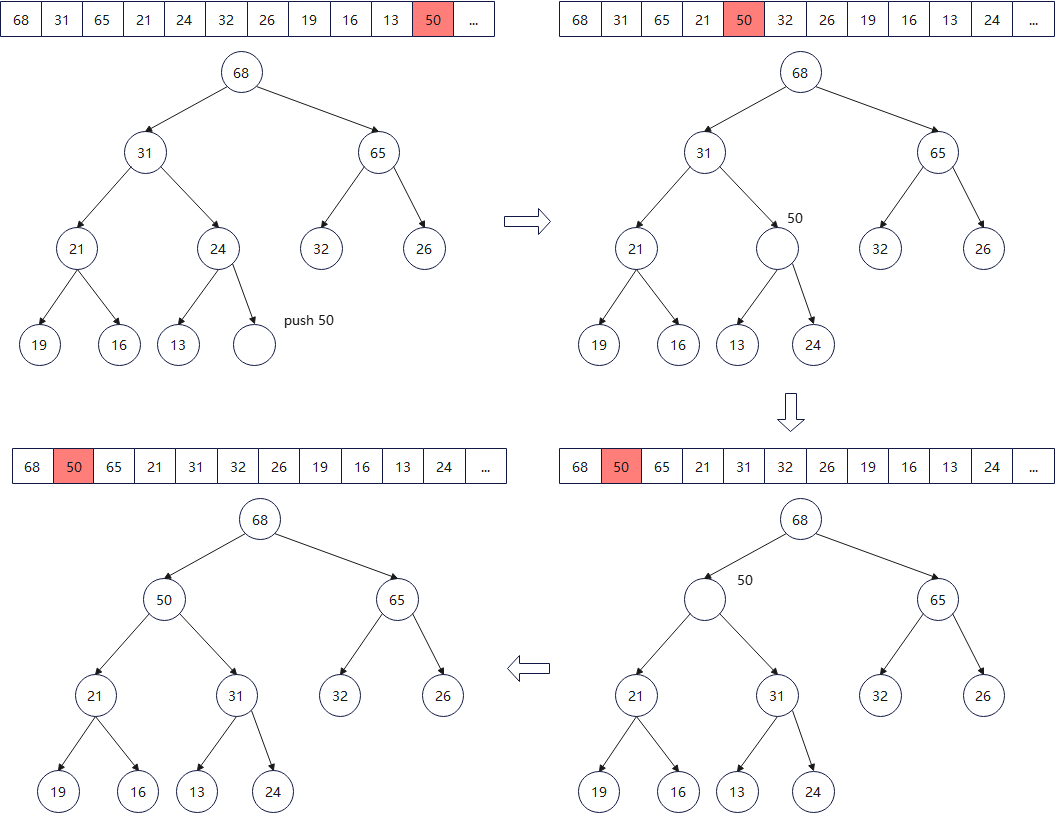
下面代码是push_heap算法实现细节。函数接受2个迭代器first和last,1)用来表示底部容器vector的头尾,2)并且新元素已经插入到底部容器尾端。如果不符合1)和2)两点,函数执行结果未知。
//-----------------------------------------------
// push_heap 算法
template <class _RandomAccessIterator, class _Distance, class _Tp>
void
__push_heap(_RandomAccessIterator __first,
_Distance __holeIndex, _Distance __topIndex, _Tp __value)
{
_Distance __parent = (__holeIndex - 1) / 2; // holeIndex父节点
// 如果父节点值 < 当前插入值value, 就把父节点值移动到洞号对应位置, 洞号移动到父节点位置
while (__holeIndex > __topIndex && *(__first + __parent) < __value) {
*(__first + __holeIndex) = *(__first + __parent);
__holeIndex = __parent;
__parent = (__holeIndex - 1) / 2; // 重新计算父节点位置
}
*(__first + __holeIndex) = __value; // 最后洞号就是插入值应该在的位置
}
template <class _RandomAccessIterator, class _Distance, class _Tp>
inline void
__push_heap_aux(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Distance*, _Tp*)
{
// 根据implicit representation heap结构特性:
// 新值必置于底部容器尾端(last-1), 即第一个洞号: (last-first)-1 (注意, 此时last已是插入元素后右移一格)
__push_heap(__first, _Distance((__last - __first) - 1), _Distance(0),
_Tp(*(__last - 1)));
}
// public接口
// 对[first, last)执行push_heap算法, 确保插入元素仍保持堆特性
// 假设[first, last)表示底部容器的头尾, 而且新元素已经插入到底部容器末尾
template <class _RandomAccessIterator>
inline void
push_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
__STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
__STL_REQUIRES(typename iterator_traits<_RandomAccessIterator>::value_type,
_LessThanComparable);
// 此函数被调用, 新元素应已经置于底部容器的尾端
__push_heap_aux(__first, __last,
__DISTANCE_TYPE(__first), __VALUE_TYPE(__first));
}
pop_heap算法
当heap移除一个元素时,max-heap如何维持堆特性?
这是pop_heap算法要解决的问题。身为max-heap,最大值位于根节点,而且pop操作取走根节点,放到底部容器vector的最后一个元素之后。
为了满足完全二叉树的特性,要将最下一层最右边的叶子节点拿掉,调换到根节点,然后从根节点开始对整个树进行调整,为这个被拿掉的节点找一个适当位置。
为满足max-heap特性(根节点key >= 子节点key),要执行一个percolate down(下溯)程序:将根节点(最大值被取走后,形成一个“洞”hole)填入上述那个失去生产空间的叶节点,再将它拿来和其两个子节点比较键值(key),并与较大子节点交换位置。如此,直到这个“洞”的key >= 左右儿子key,或者直到下放到叶子节点(没有子节点)为止。
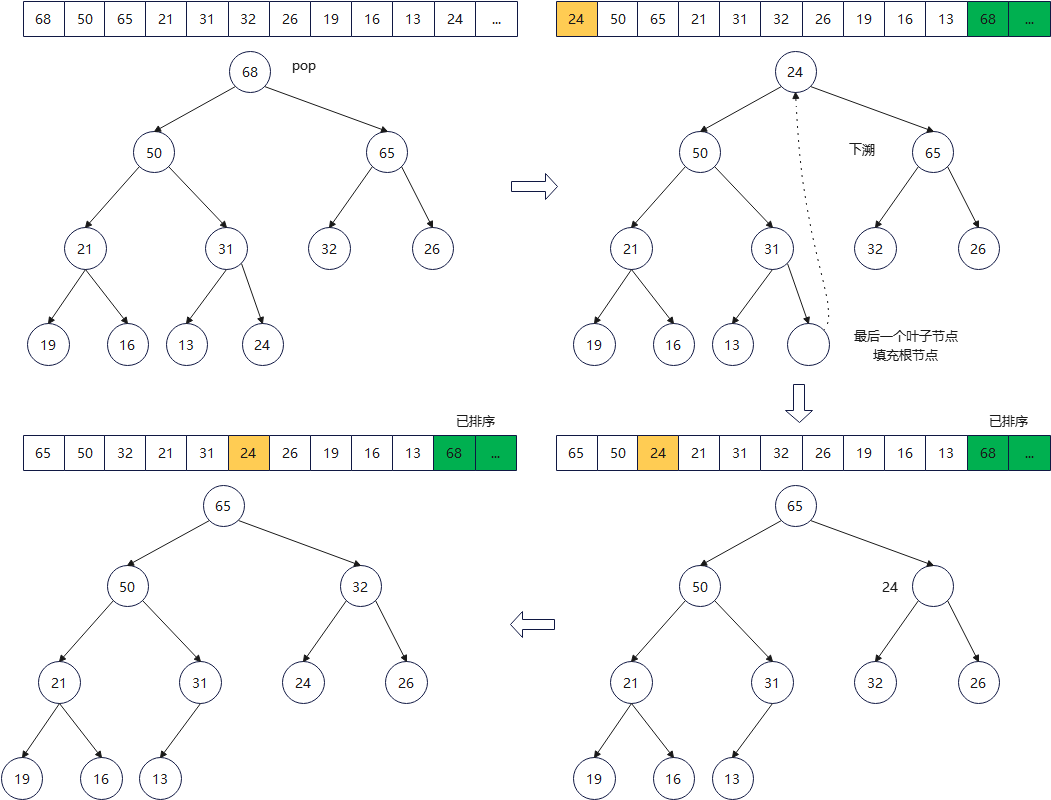
注意:示例中从max-heap中移除的68还存在vector中,不过不属于heap了。
下面代码是pop_heap实现细节。该函数接受2个迭代器,用来表示一个heap底部容器(vector)的头尾。pop_heap假设直接的元素都是通过push_heap插入heap,已经满足max-heap特性。如不符合这2个条件,pop_heap结果未定义。
//----------------------------------------------------------------
// pop_heap
// 不允许指定"大小比较标准"(比较子)的版本
// 以洞号为根节点, 重排堆, 使之符合堆特性
template <class _RandomAccessIterator, class _Distance, class _Tp>
void
__adjust_heap(_RandomAccessIterator __first, _Distance __holeIndex,
_Distance __len, _Tp __value)
{
_Distance __topIndex = __holeIndex;
_Distance __secondChild = 2 * __holeIndex + 2; // 洞节点右儿子
// 从洞节点开始, 找子树中最大的儿子, 上移至洞节点
// 将洞号往下传, 直到叶子
while (__secondChild < __len) { // 右儿子合法, 说明存在右儿子
// 比较洞节点左右2个儿子, 让secondChild代表较大子节点
if (*(__first + __secondChild) < *(__first + (__secondChild - 1)))
__secondChild--;
// 令较大儿子值为洞值, 再令洞号下移值较大子节点处
*(__first + __holeIndex) = *(__first + __secondChild);
__holeIndex = __secondChild;
// 找出新洞节点的右儿子节点
__secondChild = 2 * (__secondChild + 1);
}
if (__secondChild == __len) { // 不存在右儿子, 只有左儿子
// 令左儿子为洞值, 再令洞号下移至左儿子节点处
*(__first + __holeIndex) = *(__first + (__secondChild - 1));
__holeIndex = __secondChild - 1;
}
// 已经找到新洞号, 将欲调整值value填入目前的洞号内. 此时肯定满足次序特性.
// 下面相当于 *(first + holeIndex) = value
__push_heap(__first, __holeIndex, __topIndex, __value);
}
// 不允许指定"大小比较标准"(比较子)的版本
template <class _RandomAccessIterator, class _Tp, class _Distance>
inline void
__pop_heap(_RandomAccessIterator __first, _RandomAccessIterator __last,
_RandomAccessIterator __result, _Tp __value, _Distance*)
{
*__result = *__first; // 设尾值为首值, 于是尾值即为所求结果.
// 稍后可由客户端用底层容器的pop_back()取出尾值
// 因为原来的根节点成为洞, 堆元素个数少了1个, 因此需要重排堆
// 以根节点为子树根节点, 重新调整heap, 洞号0(树根), value是要调整的值(原来的尾值)
__adjust_heap(__first, _Distance(0), _Distance(__last - __first), __value);
}
template <class _RandomAccessIterator, class _Tp>
inline void
__pop_heap_aux(_RandomAccessIterator __first, _RandomAccessIterator __last,
_Tp*)
{
// 根据implicit representation heap的次序特性, pop操作结果应为底部容器的第一个元素.
// 因此, 首先设定欲调整值为尾值, 然后将首值交换值尾节点(即迭代器last-1指向的最后一个元素),
// 然后重新调整[first, last-1), 使之符合堆特性
__pop_heap(__first, __last - 1, __last - 1,
_Tp(*(__last - 1)), __DISTANCE_TYPE(__first));
}
// public接口
// 弹出堆顶元素, 执行下溯. 此时, 堆顶尚未从堆中移除.
// [first, last)是heap底部容器所有元素区间, 假设已经符合heap特性
template <class _RandomAccessIterator>
inline void pop_heap(_RandomAccessIterator __first,
_RandomAccessIterator __last)
{
__STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
__STL_REQUIRES(typename iterator_traits<_RandomAccessIterator>::value_type,
_LessThanComparable);
__pop_heap_aux(__first, __last, __VALUE_TYPE(__first));
}
调用pop_heap之后,最大元素只是被放置在底部容器尾端,并没有被取走。如果要取值,可以用底部容器vector提供的back();如果要移除,可以用pop_back()。
sort_heap算法
pop_heap每次能获得heap中key最大的元素,如果持续对整个heap做pop_heap操作,每次将操作范围向前缩减一个元素,这样整个程序执行完时,便有了一个递增序列。这就是堆排序(sort_heap)。
// public接口, 不支持自定义比较子版本
// 堆排序
template <class _RandomAccessIterator>
void sort_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
__STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
__STL_REQUIRES(typename iterator_traits<_RandomAccessIterator>::value_type,
_LessThanComparable);
// 每执行一次pop_heap(), 极值(STL heap中为极大值)即被放在尾端.
// 扣除尾端再执行一次pop_heap(), 次极值又被放在新尾端. 一直下去, 最后的堆排序结果
while (__last - __first > 1)
pop_heap(__first, __last--);
}
make_heap算法
严格来说,堆排序分2个步骤:1)建堆;2)一个一个元素pop到底部容器尾端,形成有序序列。
建堆是指将一段现有数据转化为heap,如何进行的呢?
这就需要用到make_heap算法。
// 不接受比较子的版本
template <class _RandomAccessIterator, class _Tp, class _Distance>
void
__make_heap(_RandomAccessIterator __first,
_RandomAccessIterator __last, _Tp*, _Distance*)
{
if (__last - __first < 2) return; // 如果长度为0或1, 不必重新排列
_Distance __len = __last - __first; // 区间长度
// 找出第一个需要重排的子树头部(最后一个non-leaf节点), 以parent标示出.
_Distance __parent = (__len - 2)/2;
while (true) {
// 重排以parent为首的子树, len是为了让 __adjust_heap() 判断操作范围
__adjust_heap(__first, __parent, __len, _Tp(*(__first + __parent)));
if (__parent == 0) return; // 走完根节点就结束
__parent--; // 下一次重排的子树, 头部向前移动一个节点
}
}
// public接口, 建堆
// 将[first, last)转换成堆
template <class _RandomAccessIterator>
inline void
make_heap(_RandomAccessIterator __first, _RandomAccessIterator __last)
{
__STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
__STL_REQUIRES(typename iterator_traits<_RandomAccessIterator>::value_type,
_LessThanComparable);
__make_heap(__first, __last,
__VALUE_TYPE(__first), __DISTANCE_TYPE(__first));
}
因此,堆排序的完整步骤是:
vector<int> vec = {2,10,-5,50,7,100,62};
// 建堆
make_heap(vec.begin(), vec.end());
// 对底部容器数据进行堆排序
sort_heap(vec.begin(), vec.end());
// 输出有序队列, 此时底部容易中数据已经有序(升序)
for (int i = 0; i < vec.size(); ++i) {
cout << vec[i];
if (i < vec.size() - 1)
cout << ",";
}
cout << endl;
heap没有迭代器
heap所有元素都遵循complete binary tree(完全二叉树)排列规则,不提供遍历功能,也不提供迭代器。
heap测试示例
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
{ // test case1: heap以vector为底部容器
int ia[9] = { 0,1,2,3,4,8,9,3,5 };
vector<int> ivec(ia, ia + 9);
make_heap(ivec.begin(), ivec.end());
for (size_t i = 0; i < ivec.size(); i++) {
cout << ivec[i] << ' '; // 9 5 8 3 4 0 2 3 1
}
cout << endl;
ivec.push_back(7);
push_heap(ivec.begin(), ivec.end());
for (size_t i = 0; i < ivec.size(); i++) {
cout << ivec[i] << ' '; // 9 7 8 3 5 0 2 3 1 4
}
cout << endl;
pop_heap(ivec.begin(), ivec.end());
cout << ivec.back() << endl; // 9
ivec.pop_back(); // 移除最后一个元素
for (size_t i = 0; i < ivec.size(); i++) {
cout << ivec[i] << ' '; // 8 7 4 3 5 0 2 3 1
}
cout << endl;
sort_heap(ivec.begin(), ivec.end());
for (size_t i = 0; i < ivec.size(); i++) {
cout << ivec[i] << ' '; // 0 1 2 3 3 4 5 7 8
}
cout << endl;
}
{ // test case2: heap以array为底部容器
int ia[6] = { 4,1,7,6,2,5 };
make_heap(ia, ia + 6);
for (size_t i = 0; i < 6; i++) {
cout << ia[i] << ' '; // 7 6 5 1 2 4
}
cout << endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号