二叉搜索树(BST)
二叉查找树有几个地方没搞明白,特别是删除结点。特写这篇文章,认真研究、记录一下。
二叉搜索树重要性质
二叉搜索树,也叫二叉树查找树,英文名Binary Search Tree,简称BST,是一颗特殊的二叉树,是查找表的一种实现。满足以下性质:
∀结点x ∈ U(U是二叉树所有结点集合),
- 如果y是x左子树的一个结点,那么y.key <= x.key;
- 如果y是x右子树的一个结点,那么y.key>=x.key;
需要注意:
-
这2条性质不仅仅只适用于当前子树根结点x和子结点的关系,而是根节点与子树所有结点的关系。
也就是说,所有右子树结点关键字不会小于根,所有左子树结点关键字不会大于根。 -
二叉树并非满二叉树或完全二叉树,更适合用于查找而非其他目的,如存储;
如果以严格递增序列插入数据,如{1,2,3,4,5}按序插入,会生成如下树形结构的二叉搜索树。明显不少满二叉树,也不是完全二叉树。
1
\
2
\
3
\
4
\
5
数据结构
结点
包含属性p - 父节点,key - 关键字,left - 左孩子, right - 右孩子。
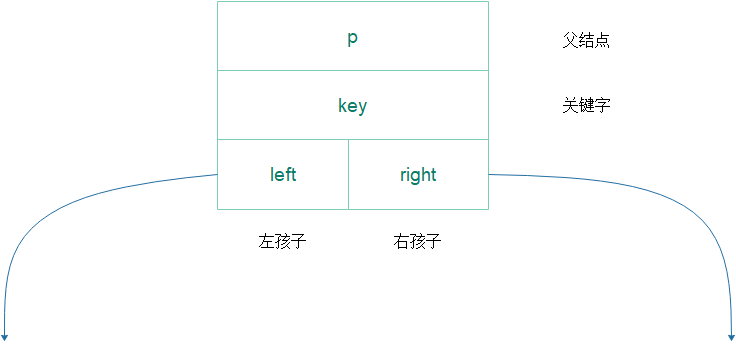
伪代码表示
Node {// 结点
p // 父结点
key // 关键字
left // 左孩子
right // 右孩子
}
二叉搜索树
以{5,2,9,1,3,7,12,null, null, null, 4, null, 8,11,20}为例,将各结点用连线连接到一起,
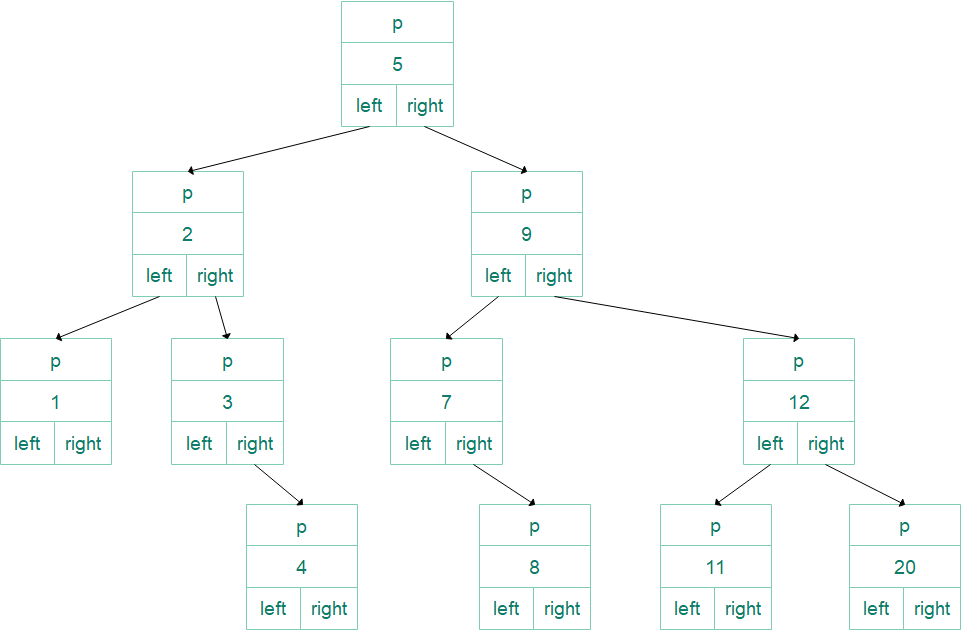
由于p、left、right这些指针大量重复,而且用箭头足以表示结点间关系,故可以省略:
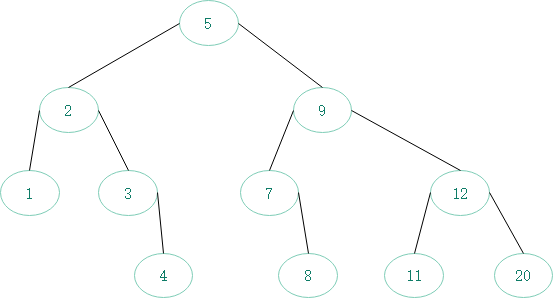
二叉搜索树的伪代码表示
Tree {
root // 根节点, 也是p=NIL的结点
}
遍历二叉搜索树
中序遍历 inorder tree walk
二叉查找树的性质,允许对其进行中序遍历得到递增序列。
注意:中序遍历(二叉树),指的是每个子树的根节点的访问顺序都是:先访问左子树,再访问根节点,最后访问右子树。
中序遍历并打印二叉搜索树的打印伪代码(递归)
INORDER-TREE-WALK(x)
if x ≠ NIL
INORDER-TREE-WALK(x.left)
print x.key
INORDER-TREE-WALK(x.rigth)
查找
查找关键字tree search
在二叉搜索树T中,查找给定关键字k的结点。
根据二叉查找树特点,从根开始,当前结点x.key > k时,k只可能在右子树,然后继续到x右子树查找;x.key < k时,左子树查找;
这样循环往下查找,结束条件:
1)找到x.key == k,说明已经成功找到;
2)x==NIL,说明树中不存在这样的结点。
TREE-SEARCH(x, k)
if x == NIL or x.key == k
return x
if k < x.key
return TREE-SEARCH(x.left, k)
else return TREE-SEARCH(x.rigth, k)
最大关键字tree maximum
沿着右子树进行查找,最后一个结点是最大关键字的结点。最大关键字结点,也称为x子树的最右结点。
TREE-MAXIMUM(x)
while x.right ≠ NIL
x = x.right
return x // 最后x.right = NIL,也就是说x没有右子树
最小关键字tree minimum
类同最大关键字查找方法。最小关键字的结点,也称x子树的最左结点。
TREE-MINIMUM(x)
while x.left ≠ NIL
x = x.left
return x // 最后x.left = NIL, 也就是说x没有左子树
后继与前驱
中序遍历二叉树得到访问序列中,当前结点的下一个结点,叫该结点的后继结点(简称后继);当前结点的前一个结点,叫该结点的前驱结点(简称前驱)。
而中序遍历整个二叉搜索树,会得到一个以全部结点关键字的非递减序列。
后继与前驱性质
记某结点为x(x∈U),其前驱为PRESUCCESSOR(x),后继为SUCCESSOR(x),有:
- PRESUCCESSOR(x).key <= x.key <= SUCCESSOR(x).key;
- 前驱是关键字≤x.key的最大结点,后继是关键字≥x.key的最小结点;
后继 SUCCESSOR
设某结点为x,后续结点y,y.key是 ≥ x.key的最小值。
y.key = min {t.key | t.key >= x.key, t∈U}, y = SUCCESSOR(x)
如何找到后继结点?
后继主要看结点有没有右子树,前驱主要看有没有左子树。
具体地,
后继与右子树有关,主要分为两类情况(前提是对应情形存在后继):
- 如果x右子树非空,x后继就是右子树的最左结点;
- 如果x右子树为空,x后继就是以x所在子树为左子树最底层祖先。
也就是说,y的左孩子也是x的祖先,x不可能位于y的右子树。而且最底层意味着,y必须是距离x最近的一个以x所在子树为左子树的祖先结点。
下图是具体几种典型情况示意图
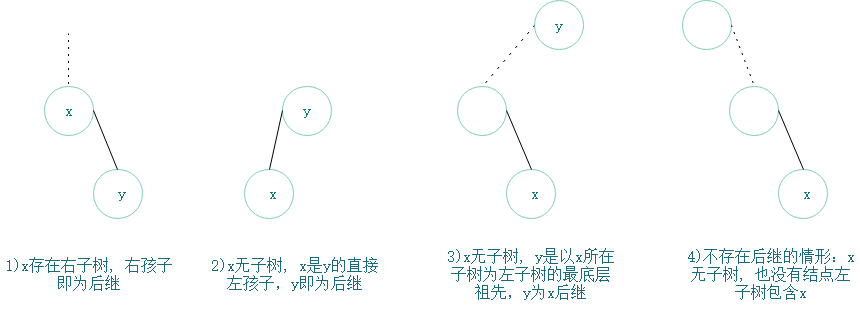
示例
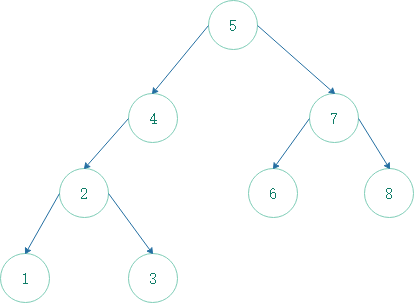
中序遍历:1,2,3,4,5,6,7,8的过程:
结点1,没有右孩子,后继是最底层以1所在子树为左子树的祖先结点2;
结点2,有右孩子,后继是右子树的最左结点3;
结点3,没有右孩子,后继是最底层以3所在子树为左子树的祖先结点4;(2以3所在子树为右子树,固2不是)
结点4,没有右孩子,后继是最底层以4所在子树为左子树的祖先结点5;
结点5,有右孩子,后继是右子树的最左节点6;
结点6,没有右孩子,后继是最底层以6所在子树为左子树的的祖先结点7;
结点7,有右孩子,后继是右子树最左结点8;
结点8,没有右孩子,没有以8所在子树为左子树的祖先结点,固8是尾节点;
求后继伪代码
TREE-SUCCESSOR(x)
if x.right ≠ NIL
return TREE-MINIMUM(x.right) // x右子树最左结点
// 从x开始自底向上, 找到第一个以x所在子树为左子树的祖先结点
y = x.p
while y ≠ NIL and x == y.right
x = y
y = y.p
return y
前驱 PRESUCCESSOR
设当前结点为x,前驱结点pre,pre.key是 ≤ x.key的最大值。
pre.key = max{t.key | t.key <= x.key, t∈U}, pre = PRESUCCESSOR(x)
如何找前驱结点?
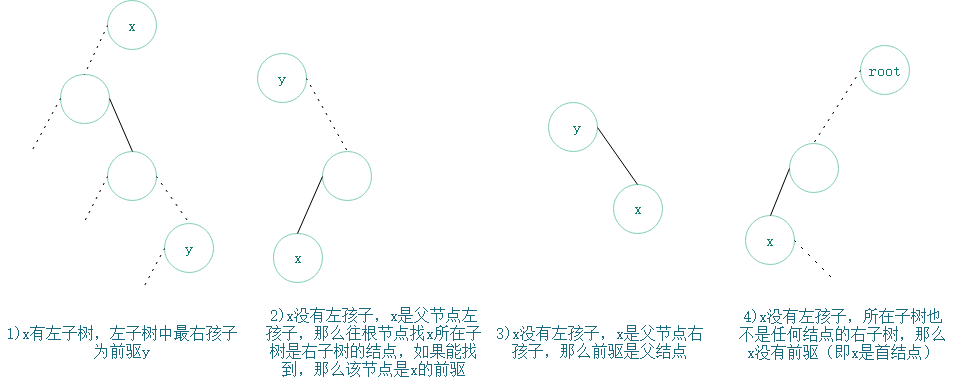
前驱分为下面2种主要情形:
1.如果当前结点x有左子树,那么x的前驱是左子树的最右孩子;
2.如果x没有左子树,那么x前驱y是x最近祖先,而且x所在子树是y的右子树。
不过,情形2也可以通过判断父结点P和x的关系:
1)如果x是P的左孩子,那么应该沿着P往上(根端)找父节点,直到找到结点Q,Q的右孩子即为x所在子树根节点。那么Q为x前驱。
2)如果x是P的右孩子,那么x前驱是P;
求前驱伪代码
TREE-PRESUCCESSOR(x)
if x.left ≠ NIL
return TREE-MAXIMUM(x.left)
else
y = x.p
while y ≠ NIL and y.left == x
x = y
y = y.p
return y
插入和删除
插入和删除操作都会改变二叉搜索树的结构,引起动态集合的变化。需要在修改后,维持二叉搜索树的性质不变。
插入 INSERT
插入结点z比较简单,分为两步:
- 按关键字搜索到合适位置;
- 在待插入位置插入新结点;
新插入的结点一定是新的叶子节点
插入结点循环版本伪代码:
TREE-INSERT(T, z)
/* 从root开始, 自上而下找到插入x.key的合适位置 */
x = T.root
while x ≠ NIL
y = x
if z.key < x.key
x = x.left
else
x = x.right
// 插入z, 作为x的子节点
z.p = x;
if y == NIL
T.root = z
if z.key < x.key
x.left = z
else
x.right = z
插入结点递归版本伪代码:
TREE-INSERT(T, z)
x = T.root
if x ≠ NIL // 非空树,递归查找应该插入z的位置,并且在对应位置插入z
FIND-INSERT(x, z)
else // 空树, 插入结点即为根结点
T.root = z
z.p = NIL
FIND-INSERT(x, z)
if z.key < x.key
if x.left ≠ NIL
FIND-INSERT(x.left, z) // x左子树继续查找
else // 已经查找到叶子结点,即当前结点x,直接插入z为x左孩子
x.left = z
z.p = x
else
if x.right ≠ NIL
FIND-INSERT(x.right, z)
else // 已经查找到叶子结点,即当前结点x,直接插入z为x右孩子
x.right = z
z.p = x
删除 DELETE
从二叉搜索树删除结点z较为复杂,需要分情况讨论:
- 如果z没有孩子,直接删除z,调整z父结点;
- 如果z只有一个孩子,那么将z的孩子替换z,调整z父结点;
- 如果z有2个孩子,原则是找z的后继y替换z(y一定是在z的右子树),不过因为涉及到后继孩子结点的调整,需要分2种情况:
1)y是z的右孩子(y没有左子树,如果右左子树必定是情形2)),那么y替换z,并且y的左孩子
2)y不是z的右孩子,而是z右子树的最左孩子。此时,y替换z,y的右孩子x提升到y原来的位置;
情形3.1:
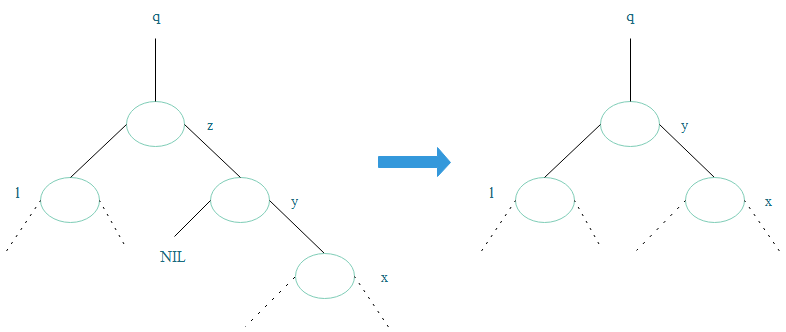
情形3.2

为了便于编程,稍作调整,改成下面4种情况:
- 如果z没有左孩子,那么用z右孩子替换z(不论右孩子是否为空NIL);
- 如果z仅有一个左孩子,那么用z左孩子替代换z;
- 如果z既有左孩子,又有右孩子,那么在z的右子树找后继y。
1)y是z右孩子(此时y必定没有左孩子),用y替换z,并且保留y的右孩子;
2)y是z位于z右子树并且不是z右孩子(此时y同样没有左孩子),必定是z右子树最左结点。
为方便二叉搜索树内部移动结点,定义子过程TRANSPLANT,表示用一颗子树替换另外一颗子树并称为其双亲的孩子结点。
用一颗v为根子树替换u为根子树的伪代码
/**
* 从二叉搜索树T中,用v子树替换u子树,并且结点u父结点原u的孩子结点替换为v结点
* 基本思想:
* 首先判断父结点
* 1.如果被替换的是根结点,就更新树的根结点信息
* 2.如果不是,则更新父结点的孩子信息
* 最后更新被替换结点包含的父结点信息
*/
TRANSPLANT(T, u, v)
if u.p == NIL // 如果被替换结点u是根结点
T.root = v
elseif u == u.p.left // 如果被替换结点是父结点左孩子
u.p.left = v
else u.p.right = v
if v ≠ NIL
v.p = u.p
/**
* 从二叉搜索树中删除结点z
*/
TREE-DELETE(T, z)
if z.left == NIL
TRANSPLANT(T, z, z.right)
elseif z.right == NIL
TRANSPLANT(T,z,z.left)
else y = TREE-MINIMUM(z.right) // y 为z右子树最左结点
if y.p ≠ z // y不是z右孩子
// 此时, y是z右子树最左结点, y.left = NIL
TRANSPLANT(T, y, y.right) // 将y右子树y.right替换y, 此时y闲置
// 将z的右孩子转换成y的右孩子
y.right = z.right
y.right.p = y
// y是z右孩子, 直接用y替换z
TRANSPLANT(T,z,y)
// 将z的左孩子替换成y的左孩子(原先y没有左孩子)
y.left = z.left
y.left.p = y


 浙公网安备 33010602011771号
浙公网安备 33010602011771号