Lecture 2: Learning to Answer Yes/no

Roadmap

1.感知器假设集

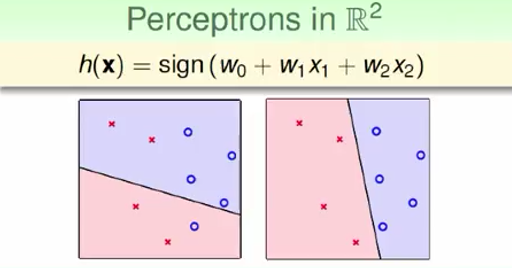
假设空间 \(H\) 到底是什么样子？

\(H\)中的一个\(h\)，\(h\)由\(\mathbf{W}\) 和 阈值决定（阈值可以作为\(w_0\)）

举个具体的栗子：

2.感知器学习算法（Perceptron Learning Algorithm, PLA）

如何选择 \(g\) ?
\(H\) = all possible perceptrons, \(g\) = ? \(\approx f\) => 直接找到与 \(f\) 相近的 \(g\) 很困难

idea：随机从一个 \(g_0\) 出发，每一轮（\(t\)）找到一个犯错的点，逐步修正\(g_t\)
具体算法：（用权重向量 \(\mathbf{W_0}\) 表示 \(g_0\)）

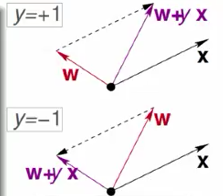
修正错误 \(\mathbf{W_{t+1}} = \mathbf{W_t} + y_nx_n\) ( (\(x_n, y_n\)) 是犯错误的点，\(\mathbf{W}\) 是分类线的法向量)

3.PLA的保证(可收敛)

假设数据线性可分，PLA何时停止更新？
\(\mathbf{W_f}\) 是理想状态下的模型
\(\mathbf{W_f W_t}\) 越大，两个向量越接近

如果每次只随机寻找犯错误的点，\(\mathbf{W_t}\)的更新会很慢，要在犯错的点中找到 \(||x_n||^2\)最大的点

PLA更新多少次会停下？T的上界是多少？
T <= 1/ \({constant^2}\) \({ constant^2 }\) = \({R^2}\) / \({\rho^2}\)

4.线性不可分的数据

如果数据线性不可分呢？
上述的保证假设数据是线性可分的，但是不一定，另外， \({\rho}\)是由\(\mathbf{W_f}\) 得出，\(\mathbf{W_f}\) 未知。

数据中可能存在少量杂讯（noise），我们尝试找一条犯错最小的线呢？

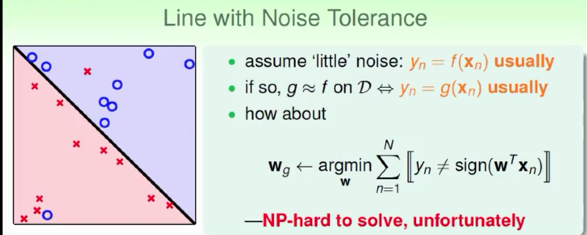
找到最完美的线，NP-hard问题。尝试找到一条差不多的线
Pocket 算法
每次找到一条新的线和当前pocket中的线进行比较，选择犯错更少的那条放入pokect中。
迭代足够多次后，停下。

PS：pocket比PLA要慢，pokect需要存储每次选择的线，并且每次需要检查出哪一条线更好。

Summary