Barreto-Naehrig curve(BN256、bn256)
总结：BN256是一种基于素数域Fp的曲线。
大多的密码学配对都来源于椭圆曲线上的Tate Pairing，自从Miller[28,29]设计出计算椭圆曲线上配对的算法后，
一系列的基于Tate Pairing的研究相继出现，通过构建合适的椭圆曲线、通过选取特定的有限群参数，旨在实现最高效的、不同安全层次的椭圆曲线配对。
其中一些改进的配对如下：eta、ate、twisted ate pairing、R-ate pairing、optimal ate pairing。
在实现128-bit安全层级上，最佳的配对友好型的曲线是Barreto-Naehrig (BN) curve[10]，
该曲线基于大小约为256 bits的，嵌入度(embedding degree) k = 12素数域内，故也称Barreto-Naehrig curve为BN256、bn256。
嵌入度(embedding degree)：反映了椭圆曲线体系向经典离散对数系统的难度。
对于BN256来说，最高效的配对是R-ate pairing[26]和optimal ate pairing[34]，optimal ate pairing算法公式如下：
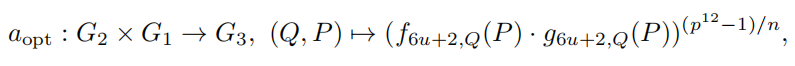
optimal ate pairing算法流程如下：
optimal ate pairing具体实现过程涉及到大量数学知识和密码学知识，有兴趣的同学可以自己查找资料弄清原理。
来源于论文：New software speed records for cryptographic pairings，该论文第二章有详细介绍。
论文原文链接：https://cryptojedi.org/papers/dclxvi-20100714.pdf
bn256的Go语言实现(GitHub链接)：https://github.com/cloudflare/bn256/blob/master/bn256.go
参考文献(摘于论文原文)：
[10] Paulo S. L. M. Barreto and Michael Naehrig. Pairing-friendly elliptic curves of prime order. In Selected Areas in Cryptography – SAC 2005, volume 3897 of Lecture Notes in Computer Science, pages 319–331. Springer, 2006.
[26] Eunjeong Lee, Hyang-Sook Lee, and Cheol-Min Park. Efficient and generalized pairing computation on abelian varieties. Cryptology ePrint Archive, Report 2008/040, 2008. http://eprint.iacr.org/2008/040/.
[28] Victor S. Miller. Short programs for functions on curves. Unpublished manuscript, 1986. http://crypto.stanford.edu/miller/miller.pdf.
[29] Victor S. Miller. The Weil pairing, and its efficient calculation. Journal of Cryptology, 17:235–261, 2004.
[34] Frederik Vercauteren. Optimal pairings. IEEE Transactions on Information Theory, 56(1).
