算法之一：老掉牙的问题

搜索有以下几种算法：

• 枚举算法：
  • 也即列举问题的所有状态从而寻找符合问题的解的方法。
  • 适合用于状态较少，比较简单的问题上。
• 广度优先搜索：
  • 从初始点开始，根据规则展开第一层节点，并检查目标节点是否在这些节点上，若没有，再将所有的第一层的节点逐一展开，得到第二层节点，如没有，则扩展下去，直到发现目标节点为止。
  • 比较适合求最少步骤或最短解序列的题目。
  • 一般设置一个队列queue，将起始节点放入队列中，然后从队列头取出一个节点，检查是否是目标节点，如不是则进行扩展，将扩展出的所有节点放到队尾，然后再从队列头取出一个节点，直至找到目标节点。
• 深度优先搜索：
  • 一般设置一个栈stack，将起始节点放入栈中，然后从栈中弹出一个节点，检查是否是目标节点，如不是则进行扩展，将扩展出的所有节点入栈，然后再从栈顶弹出一个节点，直到找到目标节点。
  • 深度优先搜索得到的第一个解，不一定是最优解。
• 双向广度优先搜索：
  • 双向搜索：从起始节点向目标节点方向搜索，同时从目标节点向起始节点方向搜索。
  • 双向搜索只能用于广度优先搜索中。
  • 双向搜索扩展的节点数量要比单向少的多。
• A*算法
  • 利用问题的规则和特点来制定一些启发规则，由此来改变节点的扩展顺序，将最有希望扩展出最优解的节点优先扩展，使得尽快找到最优解。
  • 对每一个节点，有一个估价函数F来估算起始节点经过该节点到达目标节点的最佳路径的代价。
  • 每个节点扩展的时候，总是选择具有最小的F的节点。
  • F=G+B×H：G为从起始节点到当前节点的实际代价，已经算出，H为从该节点到目标节点的最优路径的估计代价。F要单调递增。
  • B最好随着搜索深度成反比变化，在搜索深度浅的地方，主要让搜索依靠启发信息，尽快的逼近目标，而当搜索深的时候，逐渐变成广度优先搜索。
• 回溯算法：
  • 和深度优先相似，不同之处在于对一个节点扩展的时候，并不将所有的子节点扩展出来，而只扩展其中的一个。因而具有盲目性，但内存占用少。
• 搜索中的优化：
  • 在搜索前，根据条件降低搜索规模。
  • 广度优先搜索中，被处理过的节点，充分释放空间。
  • 给据问题的约束条件进行剪枝。
  • 利用搜索过程中的中间解，避免重复计算。

一、马的走法

题目：

在一个4X5的棋盘上，马的起始坐标由用户输入，求马返回初始位置的所有不同的走法的总数和步骤。马走过的位置不能重复。

 

//Chess.h

#include <vector>
using namespace std;

class Chess
{
public:
    Chess(int w, int h):width(w),height(h)
    {
        chess = new int*[w];
        for(int i = 0; i < w; i++){
            chess[i] = new int[h];
            for(int j=0; j < h; j++){
                chess[i][j] = 0;
            }
        }
    }

    int FindPath(int startx, int starty);
protected:
private:

    const static int stepx[8];   
    const static int stepy[8];

    int ** chess;
    int width;
    int height;

    struct Pos {
        Pos():x(0), y(0){}
        Pos(int _x, int _y):x(_x), y(_y){}
        int x;
        int y;
    };

    Pos startp;

    void jump(int posx, int posy, int &count, vector<Pos> &path);
};

//Chess.cpp

#include "Chess.h"

const int Chess::stepx[8]={-2, -1, 1, 2, 2, 1, -1, -2};
const int Chess::stepy[8]={1, 2, 2, 1, -1, -2, -2, -1};

int Chess::FindPath(int startx, int starty)
{
    for(int i = 0; i < width; i++)
        for(int j=0; j < height; j++)
            chess[i][j] = 0;
    startp.x = startx;
    startp.y = starty;
    vector<Pos> path;
    int count = 0;
    chess[startx][starty] = 1;
    Pos p(startx, starty);
    path.push_back(p);
    jump(startx, starty, count, path);
    return count;
}

void Chess::jump(int posx, int posy, int &count, vector<Pos> &path)
{
    for(int i = 0; i < 8; i++){
        int nextx = posx + stepx[i];
        int nexty = posy + stepy[i];
        if (nextx >= 0 && nextx < width && nexty >= 0 && nexty < height && chess[nextx][nexty] == 0) {
            chess[nextx][nexty] = 1;
            Pos p(nextx, nexty);
            path.push_back(p);
            jump(nextx,nexty,count,path);
            path.pop_back();
            chess[nextx][nexty] = 0;
        } else if (nextx == startp.x && nexty == startp.y) {
            count++;
            Pos p(nextx, nexty);
            path.push_back(p);
            printf("The %dth path : ", count);
            vector<Pos>::iterator iter;
            for(iter = path.begin(); iter != path.end(); iter++){
                Pos cur = *iter;
                printf("(%d, %d) -> ", cur.x, cur.y);
            }
            printf("\n");
            path.pop_back();
        }
    }
}

//main

#include "stdafx.h"
#include "Chess.h"

int _tmain(int argc, _TCHAR* argv[])
{
    Chess ch(4,5);
    int count = ch.FindPath(1,1);
    printf("The total number of path is : %d.\n", count);
    return 0;
}

 

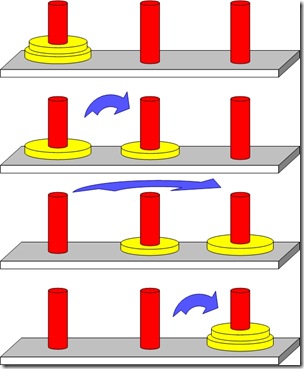
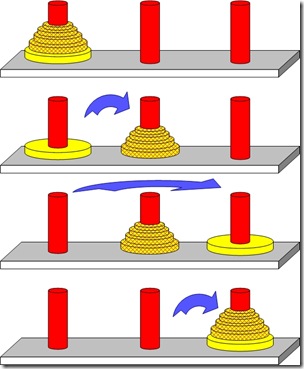
二、汉诺塔，双层汉诺塔

汉诺塔是源自印度神话里的玩具。上帝创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

从最简单的方式考虑，当仅仅有两个盘子的时候，移动过程应该如下：

当有多个盘子的时候，把除最后一个盘子以外的其他盘子看成一个整体，应用递归进行移动，过程如下：

所以得出汉诺塔的算法如下：

void hanoi(int count, char pillarA, char pillarB, char pillarC)
{
    if (count == 1) {
        printf("move from %c to %c.\n", pillarA, pillarC);
    } else {
        hanoi(count - 1, pillarA, pillarC, pillarB);
        printf("move from %c to %c.\n", pillarA, pillarC);
        hanoi(count - 1, pillarB, pillarA, pillarC);
    }
}

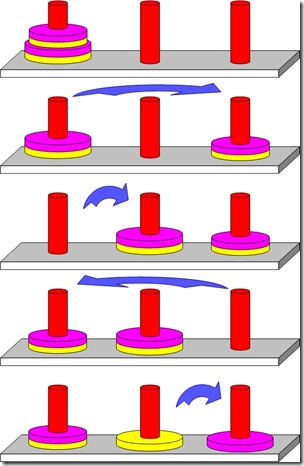
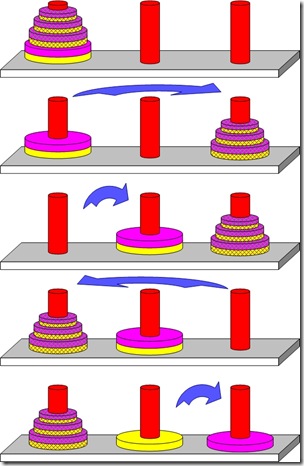
双层汉诺塔问题：双层汉诺塔是由单层汉诺塔衍生出来，相同大小的盘都有颜色不同的两片，其目的是将不同颜色的盘分别移动到右面的两个柱子上。在移动过程中，依旧是遵守大盘必须在小盘之下，而颜色顺序无限制。

当仅仅又四个盘子的情况如下：

当有多个盘子的时候，把除最后两个盘子以外的其他盘子看成一个整体，应用递归进行移动，过程如下：

双层汉诺塔实现算法如下：

void hanoi(int numofpairs, char pillarA, char pillarB, char pillarC)
{
    if (numofpairs == 1)
    {
        printf("move from %c to %c.\n", pillarA, pillarC);
        printf("move from %c to %c.\n", pillarA, pillarC);
    }
    else
    {
        hanoi(numofpairs - 1, pillarA, pillarC, pillarB);
        printf("move from %c to %c.\n", pillarA, pillarC);
        printf("move from %c to %c.\n", pillarA, pillarC);
        hanoi(numofpairs - 1, pillarB, pillarA, pillarC);
    }
}
void hanoi_double(int count, char pillarA, char pillarB, char pillarC)
{
    for (int i = count/2; i > 1; i--)
    {
        hanoi(i - 1, pillarA, pillarB, pillarC);
        printf("move from %c to %c.\n", pillarA, pillarB);
        printf("move from %c to %c.\n", pillarA, pillarB);
        hanoi(i - 1, pillarC, pillarB, pillarA);
        printf("move from %c to %c.\n", pillarB, pillarC);
    }
    printf("move from %c to %c.\n", pillarA, pillarB);
    printf("move from %c to %c.\n", pillarA, pillarC);
}

三、骑士走棋盘

骑士的走法为走日字，骑士从任意位置出发，求他要如何才能走完所有的位置。

骑士的走法，基本上可以用递归来解决，然而纯粹的递归维度很大，很没有效率，从而应用A*算法，骑士没选择下一步，优先走再下一步所能走的步数最少的一步，也即先将最难的位置走完。

//knight.h

class knight
{
public:
    knight(int w, int h):width(w), height(h)
    {
        board = new int*[width];
        for(int i = 0; i < width; i++)
        {
            board[i] = new int[height];
            for(int j = 0; j < height; j++)
            {
                board[i][j] = 0;
            }
        }
    }

    ~knight()
    {
        for(int i = 0; i < height; i++)
        {
            delete[] board[i];
        }
        delete[] board;
    }

    int travel(int startx, int starty);

    void output()
    {
        for (int i = 0; i < width; i++)
        {
            for (int j = 0; j < height; j++)
            {
                printf("%d\t", board[i][j]);
            }
            printf("\n");
        }
    }
protected:
private:
    int ** board;
    int width;
    int height;

    const static int stepx[8];
    const static int stepy[8];
};

//knight.cpp

#include "knight.h"
#include <vector>
using namespace std;

const int knight::stepx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
const int knight::stepy[8] = {1, 2, 2, 1, -1, -2, -2, -1};

int knight::travel(int startx, int starty)
{
    board[startx][starty] = 1;
    int totalsteps = width * height;

    vector<int> nextx;
    vector<int> nexty;
    vector<int> nextsteps;

    int currentx = startx;
    int currenty = starty;
    for(int step = 2; step <= totalsteps; step++)
    {
        nextx.clear();
        nexty.clear();
        nextsteps.clear();
        for(int i = 0; i < 8; i++)
        {
            int x = currentx + stepx[i];
            int y = currenty + stepy[i];
            if (x >= 0 && x < width && y >=0 && y < height && board[x][y] == 0)
            {
                nextx.push_back(x);
                nexty.push_back(y);
            }
        }

        int selected = 0;
        if (nextx.size() == 0)
        {
            return 0;
        }
        else if (nextx.size() == 1)
        {
            selected = 0;           
        }
        else
        {
            nextsteps.resize(nextx.size(), 0);
            for (int i = 0; i < nextx.size(); i++)
            {
                for (int j = 0; j < 8; j++)
                {
                    int x = nextx[i] + stepx[j];
                    int y = nexty[i] + stepy[j];
                    if (x >= 0 && x < width && y >=0 && y < height && board[x][y] == 0)
                    {
                        nextsteps[i]++;
                    }
                }
            }

            int tmp = nextsteps[0];
            selected = 0;
            for (int i = 0; i < nextsteps.size(); i++)
            {
                if (nextsteps[i] > tmp)
                {
                    tmp = nextsteps[i];
                    selected = i;
                }
            }
        }

        currentx = nextx[selected];
        currenty = nexty[selected];
        board[currentx][currenty] = step;
    }
}

int main(int argc, char ** argv){

    knight k(3, 3);
    k.travel(0, 0);
    k.output();
    return 0;
}

四、老鼠走迷宫，老鼠遍历迷宫

老鼠走迷宫，用二维矩阵中，用2表示墙壁，用1表示老鼠的行走路径，求由入口至出口的路径。

老鼠的走法有上下左右四个方向，每次选择一个方向前进，当无法前进的时候，退回选择下一个方向前进，直到走到出口为止。

由于迷宫的设计，老鼠走迷宫的入口到出口的路径可能不止一条，如何求出所有的路径？

求所有的路径其实很简单，只要在老鼠走到出口的时候不退出，仅仅显示经过的路径，然后退回上一个重新选择下一个位置就可以了。

class MouseMaze
{
public:
    MouseMaze(int* maze, int width, int height, int startx, int starty, int endx, int endy)
    {
        this->maze = maze;
        this->width = width;
        this->height = height;
        this->startx = startx;
        this->starty = starty;
        this->endx = endx;
        this->endy = endy;
    }

    int visit(int x, int y)
    {
        maze[x*width + y] = 1;
        if (x == endx && y == endy)
        {
            output();
            return TRUE;
        }

        int success = FALSE;
        if (success == FALSE && x + 1 < width && maze[(x+1)*width+y] == 0)
        {
            success = visit(x + 1, y);
        }
        if (success == FALSE && x - 1 >= 0 && maze[(x-1)*width+y] == 0)
        {
            success = visit(x - 1, y);
        }
        if (success == FALSE && y + 1 < height && maze[x*width+y+1] == 0)
        {
            success = visit(x, y + 1);
        }
        if (success == FALSE && y - 1 >= 0 && maze[x*width+y-1]== 0)
        {
            success = visit(x, y - 1);
        }

        if (success == FALSE)
        {
            maze[x*width + y] = 0;
        }

        return success;
    }

    void visitAll(int x, int y)
    {
        maze[x*width + y] = 1;
        if (x == endx && y == endy)
        {
            output();
            maze[x*width + y] = 0;
            return;
        }

        if (x+1 < width && maze[(x+1)*width+y]== 0)
        {
            visitAll(x + 1, y);
        }
        if (x-1 >= 0 && maze[(x-1)*width+y]== 0)
        {
            visitAll(x - 1, y);
        }
        if (y+1 < height && maze[x*width+y+1]== 0)
        {
            visitAll(x, y + 1);
        }
        if (y-1 >=0 && maze[x*width+y-1]== 0)
        {
            visitAll(x, y - 1);
        }

        maze[x*width + y]= 0;
    }

    void output()
    {
        if (maze == NULL)
        {
            return;
        }

        for (int i = 0; i < width; i++)
        {
            for (int j = 0; j < height; j++)
            {
                printf("%d\t",maze[i*width + j]);
            }
            printf("\n");
        }

        printf("-------------------------------------------------------------\n");
    }

protected:
private:
    int* maze;
    int width;
    int height;
    int startx;
    int starty;
    int endx;
    int endy;
};

int _tmain(int argc, _TCHAR* argv[])
{
    int maze[9][9] = {{2, 2, 2, 2, 2, 2, 2, 2, 2},
                      {2, 0, 0, 0, 0, 0, 0, 0, 2},
                      {2, 0, 2, 2, 0, 2, 2, 0, 2},
                      {2, 0, 2, 0, 0, 2, 0, 0, 2},
                      {2, 0, 2, 0, 2, 0, 2, 0, 2},
                      {2, 0, 0, 0, 0, 0, 2, 0, 2},
                      {2, 2, 0, 2, 2, 0, 2, 2, 2},
                      {2, 0, 0, 0, 0, 0, 0, 0, 2},
                      {2, 2, 2, 2, 2, 2, 2, 2, 2}};

    MouseMaze m(&maze[0][0], 9, 9, 1, 1, 7, 7);
    m.visitAll(1, 1);
    return 0;
}

五、三色旗问题

假设有一条绳子，上面有红、白、蓝三种颜色的旗子，起初绳子上的旗子颜色并没有顺序，要求将旗子排列为蓝，白，红的顺序，要如何移动，才最少。一次只能调换两个旗子。

设定一个队列，B，W，R是三种旗子的分界标，初始时，B，W在队首，R在队尾，然后从队首逐个扫描：

• 如果为白色则W+1，表示未处理部分移至白色组。
• 如果为蓝色则B与W的元素对调，B+1，W+1，表示蓝白两组都多了一个元素。
• 如果为红色则R与W的元素对调，表明红色多了一个元素。

void swap(char &a, char &b)
{
    char tmp = a;
    a = b;
    b = tmp;
}

void colorflags(char* &flags, int length)
{
    int wflag = 0;
    int bflag = 0;
    int rflag = length - 1;
    while (wflag <= rflag)
    {
        if (flags[wflag] == 'w')
        {
            wflag++;
        }
        else if(flags[wflag] == 'b')
        {
            swap(flags[bflag], flags[wflag]);
            bflag++;
            wflag++;
        }
        else if (flags[wflag] == 'r')
        {
            while (wflag < rflag && flags[rflag] == 'r')
            {
                rflag--;
            }
            swap(flags[wflag],flags[rflag]);
            rflag--;
        }
    }
}

 

六、八皇后问题

国际象棋中，皇后可以横，竖，斜直线前进，吃掉所有的棋子，如果棋盘上有八个皇后，如何放置才能使八个皇后相安无事。

class Queen
{
public:
    Queen(int n, int l):number(n), length(l)
    {
        chess = new int*[length];
        for (int i = 0; i < length; i++)
        {
            chess[i] = new int[length];
            for (int j = 0; j < length; j++)
            {
                chess[i][j] = 0;
            }
        }
        column.resize(number, 0);
        upright.resize(2*number, 0);
        downright.resize(2*number, 0);
    }

    ~Queen()
    {
        for (int i = 0; i < length; i++)
        {
            delete[] chess[i];
        }
        delete[] chess;
    }

    void output()
    {
        for (int i = 0; i < length; i++)
        {
            for (int j = 0; j < length; j++)
            {
                printf("%d\t", chess[i][j]);
            }
            printf("\n");
        }
        printf("--------------------------------------------------\n");
    }

    void placeQueen(int i)
    {
        if (i >= number)
        {
            output();
        }
        else
        {
            for (int j = 0; j < length; j++)
            {
                if (column[j] == 0 && upright[i+j] == 0 && downright[i-j+number]==0)
                {
                    chess[i][j] = 1;
                    column[j] = upright[i+j] = downright[i-j+number] = 1;
                    placeQueen(i+1);
                    chess[i][j] = 0;
                    column[j] = upright[i+j] = downright[i-j+number] = 0;
                }
            }
        }
    }
protected:
private:
    int number;
    int length;
    int ** chess;
    vector<int> column;
    vector<int> upright;
    vector<int> downright;
};

int _tmain(int argc, _TCHAR* argv[])
{
    Queen q(8, 8);
    q.placeQueen(0);
    return 0;
}