洛谷noip模拟赛 分组

题目描述

小 C 在了解了她所需要的信息之后，让兔子们调整到了恰当的位置。小 C 准备给兔子 们分成若干个小组来喂恰当的胡萝卜给兔子们吃。

此时， nn 只兔子按一定顺序排成一排，第 ii 只兔子的颜色是 a_iai​ 。由于顺序已经是被 调整好了的，所以每个小组都应当是序列上连续的一段。

在分组前，小 C 发现了一个规律：有些兔子会两两发生矛盾。并且，两只兔子会发生矛 盾，当且仅当代表他们的颜色的数值之和为一个正整数的平方。比如，1 色兔子和 2 色兔子 不会发生矛盾，因为 3 不是任何一个正整数的平方；而 1 色兔子却会和 3 色兔子发生矛盾， 因为 4 = 2^24=22。

小 C 认为，只要一个小组内的矛盾不要过大就行。因此，小 C 定义了一个小组的矛盾 值 kk ，表示在这个小组里，至少需要将这个组再一次分成 kk 个小团体；每个小团体并不需 要是序列上连续的一段，但是需要使得每个小团体内任意两只兔子之间都不会发生矛盾。

小 C 要求，矛盾值最大的小组的矛盾值 kk 不超过 KK 就可以了。当然，这样的分组方 法可能会有很多个；为了使得分组变得更加和谐，小 C 想知道，在保证分组数量最少的情况 下，字典序最小的方案是什么。你能帮帮她吗？

字典序最小的方案是指，按顺序排列分组的间隔位置，即所有存在兔子 ii 和 i + 1i+1 在 不同组的位置 ii，和其它所有相同分组组数相同的可行方案相比总有第一个不同的位置比其 它方案小的方案。

输入输出格式

输入格式：

 

从标准输入中读入数据。

输入第 1 行两个正整数 n,Kn,K。

输入第 2 行 nn 个正整数，第 ii 个数表示第 ii 只兔子的颜色 a_iai​。

 

输出格式：

 

输出到标准输出中。

输出第 1 行一个正整数 mm，为你至少需要将兔子分为多少个小组。

输出第 2 行m-1m−1个从小到大的排列的正整数，第 ii 个数 s_isi​ 表示 s_isi​ 和 s_i + 1si​+1 在 你的方案里被分到了两个小组。如果 m = 1m=1，那么请输出一个空行。

 

输入输出样例

输入样例#1： 复制 
5 2 
1 3 15 10 6
输出样例#1： 复制 
2
1

说明

【样例 1 解释】

如果将五只兔子全部分到同一个小组的话，那么 (1, 3) (3, 6) (6, 10) (10, 15) (1, 15) 均 不能分到同一个小团体；因为最多分成两个小团体，所以为了满足前 4 对限制，只能分为 {{1, 6, 15}, {3, 10}}，但此时不满足 (1, 15) ，所以不存在一种组数为 1 的方案满足全部限制。

如果将五只兔子分为两个小组的话，一种字典序最小的可行的分组方案是 {1}, {3, 15, 10, 6}，此时第二组内的小团体数量不超过 2 的一种分法是 {{3, 10}, {15, 6}}。

【数据范围】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

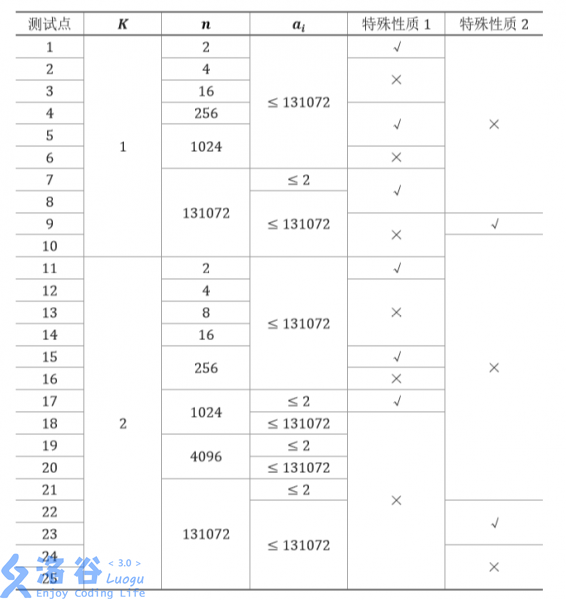
每个测试点的数据规模及特点如下表：

特殊性质 1：保证最优分组方案唯一。

特殊性质 2：保证不会有两只相同颜色的兔子。

Solution:

　　　　k==1的点很水，直接从后面贪心就好，用一个带时间戳的vis数组处理（乱搞）一下就好。

　　　　k==2的思路和前一个基本一样，只不过用一个并查集维护一下和当前颜色冲突的两个颜色是否也冲突，如果它俩也冲突那么说明需要重新分一个组，否则可以继续，直到出现不合法状态或找完为止。

 1 #pragma GCC optimize("O3")
 2 #include <iostream>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <algorithm>
 6 #include <vector>
 7 using namespace std;
 8 int read() {
 9     int s=0,f=1;
10     char ch=getchar();
11     for( ; ch<'0'||ch>'9'; f=(ch=='-')?-1:f,ch=getchar()) ;
12     for( ; ch>='0'&&ch<='9' ;s=s*10+(ch^48),ch=getchar()) ;
13     return s*f;
14 }
15 int n,k,Color[262505],Ans[262505],Fa[262505*2],vis[262505];
16 vector<int> Match[262505];
17 namespace ONE {
18     void work() {
19         Ans[0]=1;
20         for(int i=n; i; --i) {
21             bool pd=true;
22             for(int j=512; j&&pd; --j) {
23                 if(j*j<Color[i]) break;
24                 if(vis[j*j-Color[i]]==Ans[0]) pd=false;
25             }
26             if(!pd) Ans[Ans[0]++]=i;
27             vis[Color[i]]=Ans[0];
28         } printf("%d\n",Ans[0]);
29         for(int i=Ans[0]-1; i; --i) printf("%d ",Ans[i]);
30     }  
31 }
32 namespace TWO {
33     void init() {for(int i=1; i<=n*2; ++i) Fa[i]=i;}
34     int find(int x) {return x==Fa[x]?x:Fa[x]=find(Fa[x]);}
35     void Union(int x,int y) {
36         x=find(x),y=find(y);
37         Fa[x]=y;
38     }
39     void work() {
40         init(); Ans[0]=1;
41         for(int i=n; i; --i) {
42             bool pd=true;
43             for(int j=512; j&&pd; --j) {
44                 if(j*j-Color[i]<0) break;
45                 if(vis[j*j-Color[i]]==Ans[0]) {
46                     int now=j*j-Color[i];
47                     for(int k=0; k<Match[now].size()&&pd; ++k) {
48                         if(find(i)==find(Match[now][k])) {pd=false; continue;}
49                         Union(i+n,Match[now][k]),Union(i,Match[now][k]+n);
50                     }
51                 }
52             } 
53             if(!pd) Ans[Ans[0]++]=i;
54             if(vis[Color[i]]!=Ans[0]) {
55                 vis[Color[i]]=Ans[0];
56                 Match[Color[i]].clear();
57             } Match[Color[i]].push_back(i);
58         } printf("%d\n",Ans[0]);
59         for(int i=Ans[0]-1; i; --i) printf("%d ",Ans[i]);
60     }
61 }
62 int main() {
63     n=read(),k=read();
64     for(int i=1; i<=n; ++i) Color[i]=read();
65     if(k==1) ONE::work();
66     else TWO::work();
67     return 0;
68 }

 

posted @ 2017-11-02 16:46  Forever_goodboy  阅读(493)  评论(0)  编辑  收藏  举报