弱题题解

题面：

题目描述

有M个球，一开始每个球均有一个初始标号，标号范围为1～N且为整数，标号为i的球有ai个，并保证Σai = M。

每次操作等概率取出一个球（即取出每个球的概率均为1/M），若这个球标号为k（k < N），则将它重新标号为k + 1；若这个球标号为N，则将其重标号为1。（取出球后并不将其丢弃）

现在你需要求出，经过K次这样的操作后，每个标号的球的期望个数。

输入

第1行包含三个正整数N，M，K，表示了标号与球的个数以及操作次数。

第2行包含N个非负整数ai，表示初始标号为i的球有ai个。

输出

应包含N行，第i行为标号为i的球的期望个数，四舍五入保留3位小数。

样例输入

2 3 2
3 0

样例输出

1.667
1.333
考试时想到了一个最暴力的dp转移，竟然骗到了55分，数据太水QAQ。。。。。。
递推公式其实很好想，f[i][j]代表到第i个球到第j次的期望个数，但是发现第二维没有办法开，于是滚动数组，用O（n*k）的效率转移
f[i][j]=f[i][j^1]+f[i-1][j^1]/m-f[i][j^1]/m;
　　　　=(m-1)/m*f[i][j^1]+f[i-1][j^1]

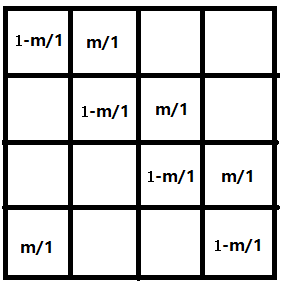
发现这个玩意其实可以矩阵优化，先构造矩阵，但是又发现如果普通矩阵n^3的效率肯定要T，
其实这个矩阵不管自乘多少次第i行都是由第i-1行右移一位，所以只需要算出第一行在递推转移即可
于是时间为O(n^2*log)

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,k;
double f[1005],a[1005][1005],temp[1005];
void init() {
    double p1=(double)(m-1)/m,p2=(double)1/m;
    for(int i=1; i<=n; i++) {
        a[i][i]=p1;
    }
    for(int i=1; i<n; i++) {
        a[i][i+1]=p2;
    }
    a[n][1]=p2;
}
int main() {
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1; i<=n; i++) {
        scanf("%lf",&f[i]);
    }
    init();
    for(; k; k>>=1) {
        if(k&1) {
            for(int i=1; i<=n; i++) {
                temp[i]=0;
                for(int j=1; j<=n; j++) {
                    temp[i]+=f[j]*a[j][i];
                }
            }
            for(int i=1; i<=n; i++) {
                f[i]=temp[i];
            }
        }
        for(int i=1; i<=n; i++) {
            temp[i]=0;
            for(int j=1; j<=n; j++) {
                temp[i]+=a[1][j]*a[j][i];
            }
        }
        for(int i=1; i<=n; i++) {
            a[1][i]=temp[i];
        }
        for(int i=2; i<=n; i++) {
            a[i][1]=a[i-1][n];
            for(int j=2; j<=n; j++) {
                a[i][j]=a[i-1][j-1];
            }
        }
    }
    for(int i=1; i<=n; i++) {
        printf("%0.3lf\n",f[i]);
    }
    return 0;
}