2020面向对象设计与构造 第一单元 博客总结
面向对象设计与构造 第一单元 总结
一、程序结构分析
1. 第一次作业:简单多项式的求导
本次作业是首次对Java面向对象项目的尝试,共包括三次架构设计。
(1)第一次构思
由于第一次作业整体难度不高,笔者最先想到的是使用往常C语言的面向过程思维,通过对输入字符串的匹配,将多项式的每一项拆分为系数和指数存放入容器,然后进行简单的合并优化后输出,即使用“一main到底”方法。
这样设计架构虽然可以通过测试,但并没有实现对象化的封装,在时间充足的情况下,笔者决定尝试面向对象的设计,因此该设想被放弃。
(2)第二次架构实现
第二次架构设计了Func接口,实现类有Const和Pow;设计了Expression 类用HashMap来存放表达式,Term类来存放系数和幂函数。
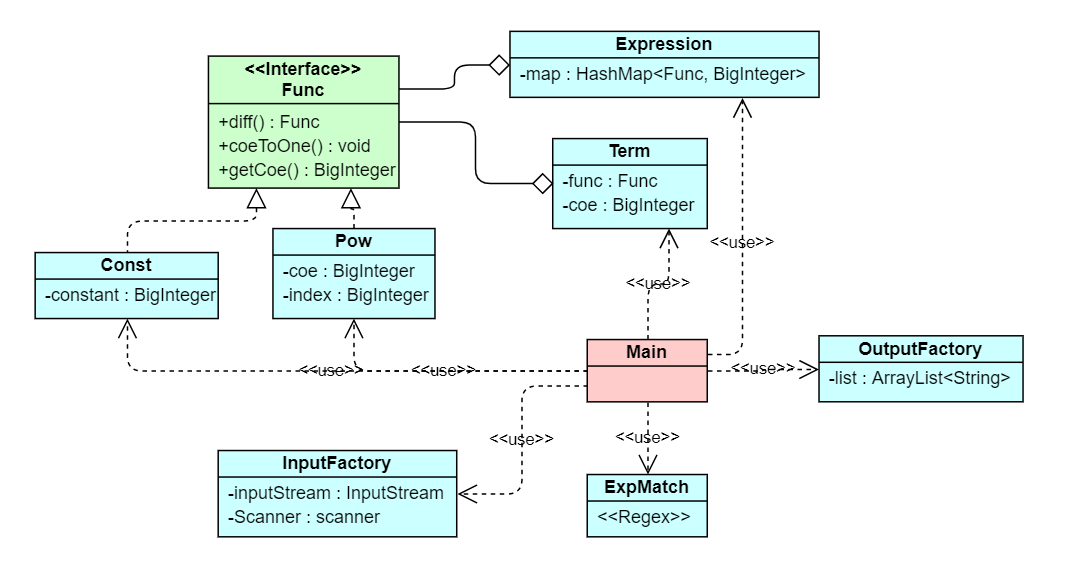
下表是本次设计代码量和结构分析,可见本次设计的复杂度较为理想。
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Total | 50.0 | 67.0 | 75.0 |
| Average | 1.31 | 1.76 | 1.97 |
| class | Total Lines | Src Lines | OCavg | WMC |
|---|---|---|---|---|
| Total | 446 | 381 | 73 | |
| Average | 49.56 | 42.33 | 1.92 | 9.12 |
该版本于作业开放周的周三完成并且通过中测,距离周六中测截止还有一定时间(同时自己在灌水群不小心知道了后续迭代的部分内容)。因此笔者在开学第一周任务量还没那么大的情况下,脑洞大开,进行了对后续迭代可能性的猜测。
- 已有的幂函数和常数函数,属于六大基本初等函数,因此扩展必须易于支持三角函数、指数函数、对数函数、反三角函数。
- 函数的自变量可能不是字母
x,要考虑兼容其他名称变量的情况,比如自变量m、j。(函数也可能不只有一个自变量,传说中的多元函数求导) - 幂函数的底数可能为表达式,除常数函数外的函数同样拥有此类特征。笔者想了一段时间才反应过来这种表达式本质上是复合函数。
(指数也可能是个表达式,但是笔者数分功底太差,都忘记手算该怎么求了,所以代码没有考虑迭代这种情况) - 函数都支持四则运算,加减可以合并为加法,乘除可以合并为乘法。
然后对该版本程序可扩展性进行了评价,分析得到如下几点不足之处。
- 幂函数类
Pow的成员变量包含系数和指数两部分,其中系数部分与常数类Const相重复。 - 输入处理使用了多个子正则表达式组合而成的大型正则表达式,很不利于长表达式的识别。
- 项类
Term如果对上述复合函数进行求导,单纯包含一个幂函数和一个系数根本无法实现,表达式类只有一个HashMap就更显乏力,这一点也可以从简化的UML类图看出。
(3)第三次架构实现
第三次完善(重构)了设计,基本支持除了多元函数求导外的扩充,周六下午才正式完成测试提交中测。
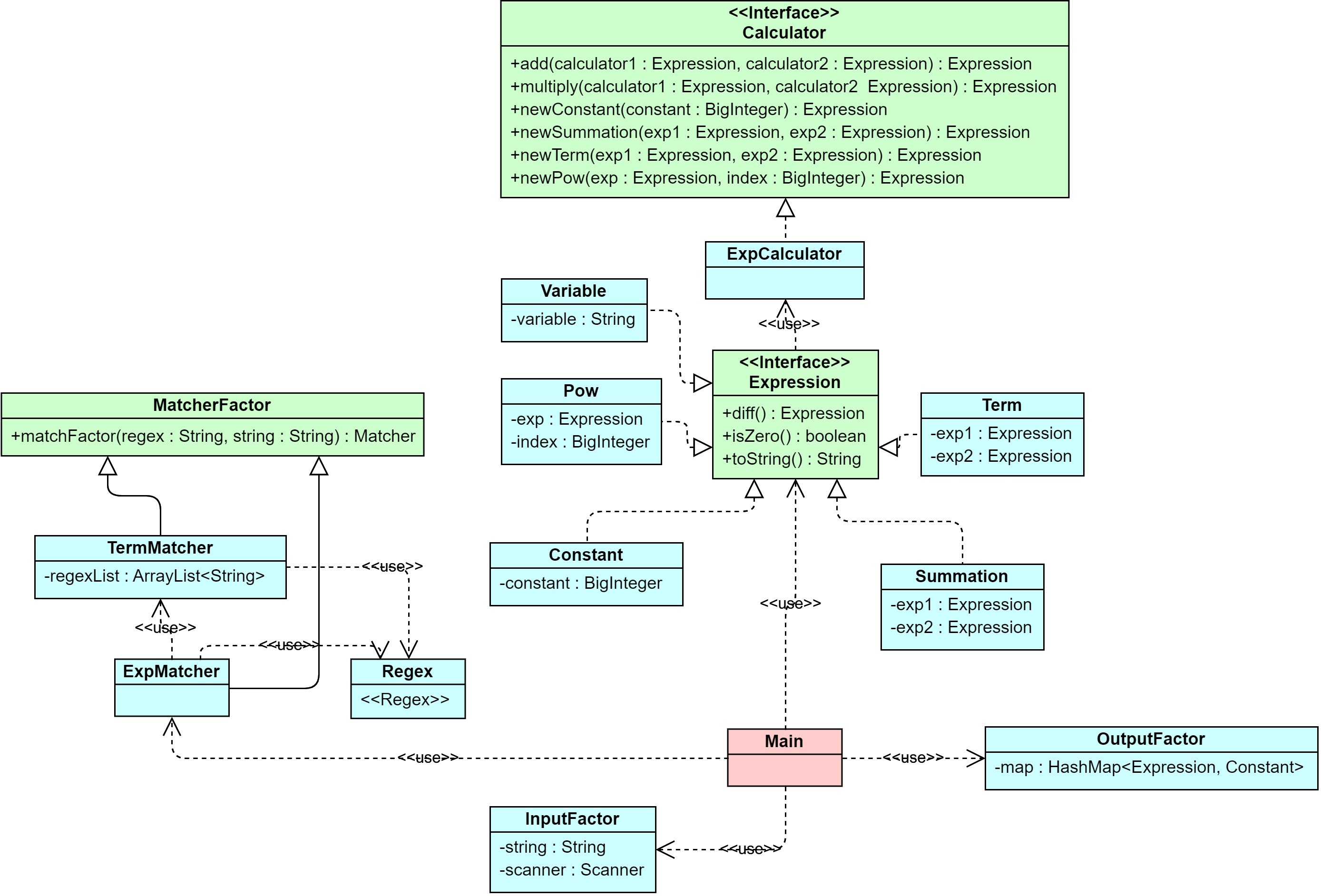
代码量有了明显的提升,复杂度也较为理想,重要的是可扩展性变强了。表格只列举了部分复杂度较高的方法。
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| ExpCalculator.add(Expression,Expression) | 6.0 | 5.0 | 7.0 |
| ExpCalculator.multiply(Expression,Expression) | 12.0 | 13.0 | 13.0 |
| Pow.toString() | 5.0 | 5.0 | 5.0 |
| Total | 114.0 | 130.0 | 141.0 |
| Average | 1.62 | 1.85 | 2.01 |
| class | Total Lines | SrC Lines | OCavg | WMC |
|---|---|---|---|---|
| main.expression.ExpCalculator | 104 | 86 | 3.29 | 23.0 |
| main.expression.function.Constant | 60 | 48 | 1.33 | 12.0 |
| main.expression.function.Pow | 84 | 71 | 1.8 | 18.0 |
| main.expression.function.Summation | 42 | 34 | 1.5 | 9.0 |
| main.expression.function.Term | 49 | 41 | 1.83 | 11.0 |
| main.expression.function.Variable | 49 | 39 | 1.29 | 9.0 |
| main.input.ExpMatcher | 67 | 61 | 5.5 | 11.0 |
| main.input.InputFactor | 30 | 24 | 1.5 | 6.0 |
| main.input.MatcherFactor | 11 | 9 | 1.0 | 1.0 |
| main.input.Regex | 35 | 28 | 1.0 | 6.0 |
| main.input.TermMatcher | 49 | 43 | 2.67 | 8.0 |
| main.Main | 28 | 24 | 1.5 | 3.0 |
| main.output.Double | 19 | 15 | 1.0 | 3.0 |
| main.output.OutputFactor | 73 | 66 | 2.75 | 11.0 |
| Total | 728 | 606 | 131.0 | |
| Average | 48.53 | 40.40 | 1.87 | 9.36 |
本架构有几个优势的地方,同时也存在不足。
- 将乘积项与加和项也实现
Expression接口,可以实现乘积和加和的求导法则。 - 对于每个类的
toString()方法,特判是否为0、1,可以提升结果的性能,但是弊端是导致所有类的该方法复杂度都过高。 - 笔者在设计时并未考虑到二叉树,最后设计出的其实依然是二叉树结构,可以从UML图的
TermSummation成员看出。为了化简不对其进行遍历,笔者在ExpCalculator类的Multiply(Expression, Expression)方法中,特意将二叉树的右节点设为单一的函数或常量,便于循环取出每一个因子进行合并优化。 - 表达式运算类的方法由于加入了过多化简的逻辑,因此复杂度与耦合度都远高于其他方法。
2. 第二次作业:加入正余弦函数的简单表达式求导
第二次作业有了第一次作业的基础,方便表达式接口的拓展,得到正确的结果还是很容易的,但优化较困难。程序主体分为表达式、输入处理和输出优化。与第一次作业作了明显改动的地方已用红色标记。
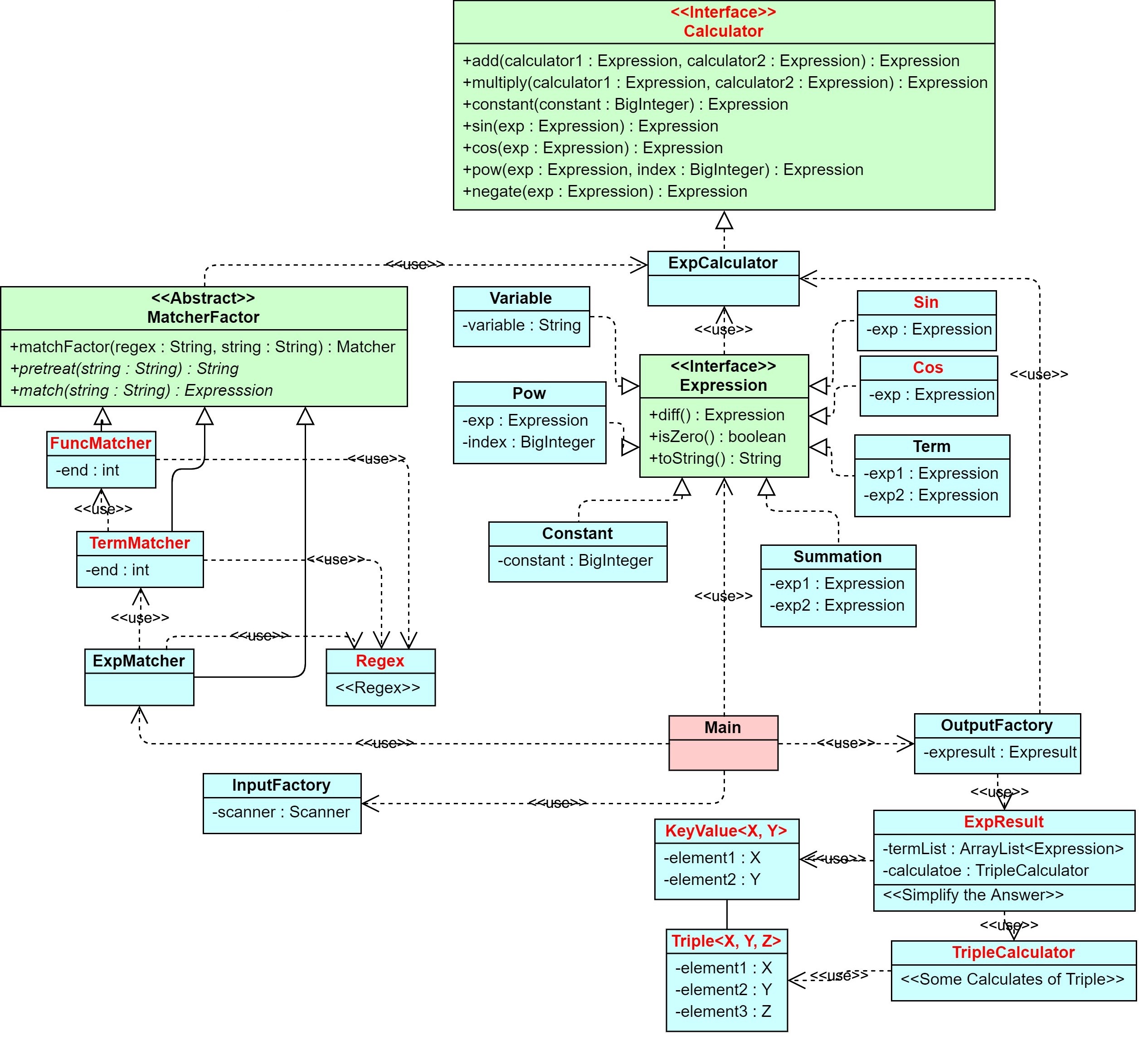
本次优化方法十分冗余复杂,所以代码增加量非常大。复杂度和耦合度有微小提高。表格只列举了部分复杂度较高的方法。
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| ExpCalculator.add(Expression,Expression) | 6.0 | 5.0 | 7.0 |
| ExpCalculator.multiply(Expression,Expression) | 12.0 | 13.0 | 13.0 |
| Pow.toString() | 6.0 | 7.0 | 8.0 |
| Term.toString() | 8.0 | 8.0 | 9.0 |
| FuncMatcher.funcMatch(String,int) | 4.0 | 6.0 | 9.0 |
| TripleCalculator.same(BigInteger,BigInteger) | 6.0 | 9.0 | 10.0 |
| Total | 188.0 | 247.0 | 273.0 |
| Average | 1.72 | 2.26 | 2.50 |
| class | Total Lines | SrC Lines | OCavg | WMC |
|---|---|---|---|---|
| main.expression.ExpCalculator | 114 | 96 | 3.71 | 26.0 |
| main.expression.function.Constant | 60 | 48 | 1.33 | 12.0 |
| main.expression.function.Cos | 37 | 29 | 1.2 | 6.0 |
| main.expression.function.Pow | 85 | 72 | 1.9 | 19.0 |
| main.expression.function.Sin | 41 | 33 | 1.4 | 7.0 |
| main.expression.function.Summation | 42 | 34 | 1.5 | 9.0 |
| main.expression.function.Term | 53 | 45 | 2.17 | 13.0 |
| main.expression.function.Variable | 49 | 39 | 1.29 | 9.0 |
| main.input.InputFactory | 25 | 21 | 2.0 | 4.0 |
| main.input.parser.ExpMatcher | 73 | 67 | 4.33 | 13.0 |
| main.input.parser.FuncMatcher | 107 | 98 | 3.0 | 18.0 |
| main.input.parser.MatcherFactory | 17 | 12 | 1.0 | 1.0 |
| main.input.parser.TermMatcher | 64 | 57 | 2.5 | 10.0 |
| main.input.Regex | 53 | 43 | 1.0 | 9.0 |
| main.Main | 30 | 26 | 1.5 | 3.0 |
| main.output.ExpResult | 143 | 134 | 4.5 | 27.0 |
| main.output.groups.KeyValue | 19 | 15 | 1.0 | 3.0 |
| main.output.groups.Triple | 38 | 31 | 1.17 | 7.0 |
| main.output.groups.TripleCalculator | 182 | 172 | 4.0 | 36.0 |
| main.output.OutputFactory | 58 | 52 | 2.0 | 6.0 |
| Total | 1318 | 1141 | 238.0 | |
| Average | 59.91 | 51.86 | 2.18 | 11.9 |
由于第一次做了很多铺垫,错误格式处理较容易,所以设计重心放在了优化输出上。
- 由分析可知,新增的复杂度和耦合度几乎都来自三元组输出优化,笔者对优化确实没有想出好的实现方法,在合并同类项后,使用简单的三角公式进行化简,双重循环寻找可以合并的两项,但没有考虑化简结果是否将输出简短,最后至少可以实现
m * sin(x)**2 + n * cos(x)**2多次幂的合并以及m - n * sin(x)**2和m - n * cos(x)**2的化简(m, n是同号的)。 - 改写部分表达式运算的方法,在构造幂函数和三角函数时判断内部因子类型,加入取反方法,方便对负号开头表达式的处理。
- 输入采用层次化处理,整体对表达式匹配,以
+为分隔;子匹配类对乘积项匹配,以*为分隔;使用Regex类的正则表达式对因子进行匹配。匹配的层次关系可以从UML图看出。这样匹配的优势是可以在匹配失败(比如匹配结果是null,或匹配开始没有识别到指定的分隔符号)时判定为格式错误,而不需要在开始对格式进行判断。 - 除了第一次的残留问题外,新增复杂度高的类都来自优化输出。
- 这次作业的优化出现了严重的Bug,将在程序Bug分析部分说明。
3. 第三次作业:加入嵌套因子(括号)的表达式求导
在第二次作业的基础上,第三次作业几乎只需要对括号情况进行递归处理,就可以得到正确结果。表格只列举了部分复杂度较高的方法。

因为没有对三角函数进行特定优化,代码量略少于第二次。复杂度有所上升。
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| ExpCalculator.add(Expression,Expression) | 6.0 | 5.0 | 7.0 |
| ExpCalculator.multiply(Expression,Expression) | 12.0 | 15.0 | 15.0 |
| Pow.toString() | 5.0 | 5.0 | 7.0 |
| Term.toString() | 8.0 | 6.0 | 13.0 |
| Term.equals(Object) | 12.0 | 8.0 | 12.0 |
| Summation.equals(Object) | 12.0 | 8.0 | 12.0 |
| FuncMatcher.funcMatch(String,int,Matcher) | 1.0 | 14.0 | 17.0 |
| Total | 185.0 | 230.0 | 270.0 |
| Average | 1.86 | 2.32 | 2.72 |
| class | Total Lines | SrC Lines | OCavg | WMC |
|---|---|---|---|---|
| main.expression.ExpCalculator | 134 | 110 | 4.42 | 31.0 |
| main.expression.function.Constant | 60 | 48 | 1.33 | 12.0 |
| main.expression.function.Cos | 57 | 47 | 1.57 | 11.0 |
| main.expression.function.Pow | 90 | 77 | 1.9 | 19.0 |
| main.expression.function.Sin | 60 | 50 | 1.71 | 12.0 |
| main.expression.function.Summation | 94 | 83 | 2.75 | 22.0 |
| main.expression.function.Term | 122 | 111 | 3.75 | 30.0 |
| main.expression.function.Variable | 49 | 39 | 1.28 | 9.0 |
| main.input.InputFactory | 33 | 29 | 2.5 | 5.0 |
| main.input.parser.ExpMatcher | 79 | 72 | 3.25 | 13.0 |
| main.input.parser.FuncMatcher | 121 | 112 | 3.5 | 21.0 |
| main.input.parser.MatcherFactory | 19 | 13 | 1.0 | 1.0 |
| main.input.parser.TermMatcher | 67 | 60 | 2.5 | 10.0 |
| main.input.Regex | 59 | 47 | 1.0 | 11.0 |
| main.Main | 30 | 26 | 2.0 | 4.0 |
| main.Simplify | 150 | 141 | 4.83 | 29.0 |
| Total | 1252 | 1082 | 240.0 | |
| Average | 69.56 | 60.11 | 2.42 | 15.0 |
- 从UML图可以看出,输入匹配中每个类都有成员变量
end。由于笔者匹配字符串时不会对其进行拆分,而是每次识别到一个因子、一个项、一个子表达式因子后使用substring(String)将匹配到的部分删去,所以需要在使用内层匹配类后得到匹配的终点,方便外层匹配类对字符串进行缩减。 - 将表达式因子与正余弦函数、幂函数和常数等价为同类元素,以
(开头,递归调用ExpMatcher类对其匹配,返回后以)作为表达式因子正常结束的标志。因此判断格式错误依旧与第二次一样。 - 修改了
ExpCalculator类中的乘法,让每个Term对象的右节点为常数(没有常数时就是一个普通的因子),这样做便于直接提取每一项的系数。修改了正余弦方法,用于对sin(0)、cos(0)和cos(-[term])进行化简。 - 重写
Summation类和Term类的hashCode()和equals(Object)方法,便于使用HashMap直接对项内同底幂函数和表达式内同类项进行合并,方法封装在新增的Simplify类中。 - 除了遗留问题外,新增复杂度也主要体现在合并同类项的部分,以及对表达式因子的匹配部分。笔者个人没有想到不破坏架构实现优化的方式,采用了牺牲架构换取优化的策略。
二、程序Bug分析
1. 线下自测
- 优化前,构造一些基本数据和边界数据对程序进行测试,先观察结果是否有格式问题,进而检查正确性。
- 优化过程中,每加入一次优化就对程序进行优化的测试,同时测试功能。
- 笔者从三次作业角度,发现个人容易出现Bug的几个地方。
- 输入匹配时的end计算不正确,导致字符串修改错误,出现误判格式错误。
- 输入匹配使用
CharAt(int)方法时没有考虑是否为空串,导致异常。 ExpCalculator类的乘法和加法方法在首次测试时陷入了递归死循环导致爆栈。- 第三次作业进行优化时,忘记考虑底数不能为表达式和常数,导致
(x+1)**5、1**9等类似情况出现。
2. 提交后发现的Bug
笔者三次作业的中测从未出现Bug,第一次和第三次的强测、互测未被发现Bug,但第二次出现了严重的问题。
首先,在第二次作业互测开放的下午,笔者测试自己程序发现了优化的问题,在化简两项三角函数时,会产生一个新的项,笔者并没有考虑新的项是否本身存在于HashMap中,而是直接使用put(Triple<>)方法将原本存在的内容覆盖,这样会导致最终结果的系数完全不正确,比如sin(x)**2 + cos(x)**2 + 2,经过笔者的化简后,结果为1。
在强测结果公开后,笔者发现自己还有误判格式错误的Bug,即没有考虑sin (x)的情况。
分析两个Bug,笔者认为原因是自己在第一次作业的铺垫下过于自信,没有仔细研读指导书,没做太多的测试。
三、 互测发现其他人Bug策略
1. 第一次互测
笔者第一次互测房间内1个Bug都没有发现,全屋都零伤亡。
2. 第二次互测
第二次互测,笔者使用了Python生成数据和自己构造的强数据,用Python的Sympy库对拍,发现了如下Bug,但有的Bug笔者并不知道是什么问题所致(代码有点难读)。
- 连乘
x不能正确识别,判定为格式错误。 - 化简三角函数不正确。
- 其他求导结果、格式判断错误。
3. 第三次互测
第三次互测,笔者继续沿用第二次的策略,强数据主要是自测发现的Bug以及和同学交流后总结的一些常见Bug,发现了屋内有如下Bug。
-
在不做优化的前提下,对0求导输出没有加上
+,x+0结果为+10。 -
(x+1)*(x+2)*(x+3)*(x+4)*(x+5)*(x+6)*(x+7)*(x+8)*(x+9)*(x+10)求导结果错误,但是笔者去掉一个因子或者改变因子类型后均没有再发现Bug,可谓玄学。 -
括号内部嵌套常数加减,外部乘表达式时,会出现括号嵌套错位置的Bug。
-
输出出现中间项包含
-的格式错误Bug。 -
并没有发现常见超时、爆栈的Bug。
四、总结
笔者经过第一单元的练习,收获颇丰。
- 学会使用git管理自己的版本仓库。
- 在寒假还没接触过Java语言,现在已经对Java入门,了解了基本语法、容器、泛型等知识。
- 能够自己思考如何设计架构保证扩展性,使用一部分面向对象的思想来解决问题。
- 代码量有了巨大提升,首次完成工程化项目设计。
- 代码风格相比一年前,提升巨大。
- 构造测试用例,考虑边界数据。
- 学会了一些辅助评测的工具。
同时依然存在很多不足。
- 在对程序进行优化时没有考虑程序的复杂度,把方法写得十分臃肿,导致复杂度和耦合度骤增,目前还没有学到解决逻辑过多问题的办法。
- 还没使用过异常处理对程序的异常进行捕捉。
- 研读其他人代码的效率太低。
- 对架构盲目自信,往往会自食其果,应当仔细研读指导书,做足测试。
整体来看,对OO这门课的体验还是很好的,希望自己再接再厉。
这也是笔者的第一篇博客,特此纪念。


