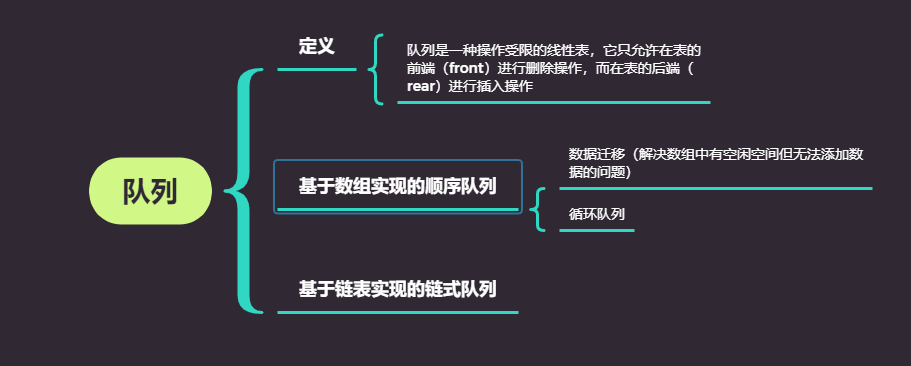
队列,一种"公平"的数据结构
路过一家奶茶店,由于生意火爆,门口的排着长长的队伍,先排队的人先买到奶茶,然后再轮到下一个,秩序井然。有没有一种数据结构能体现”先来后到“这种顺序呢?
当然有,那就是队列。先看一下定义:队列是一种操作受限的线性表,它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作。只能在表的最前端删除,最后端插入,这和排队买奶茶中先给最前面的人做奶茶,新来的只能在最后面排队一样,相对“公平”。
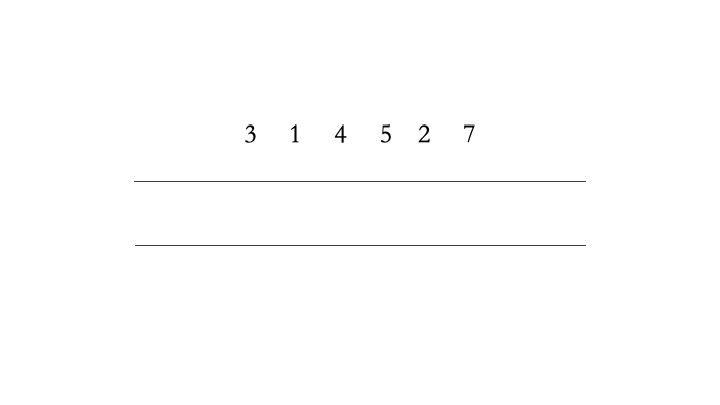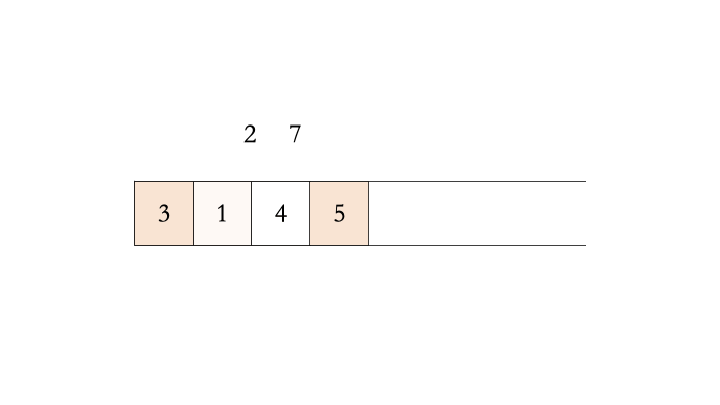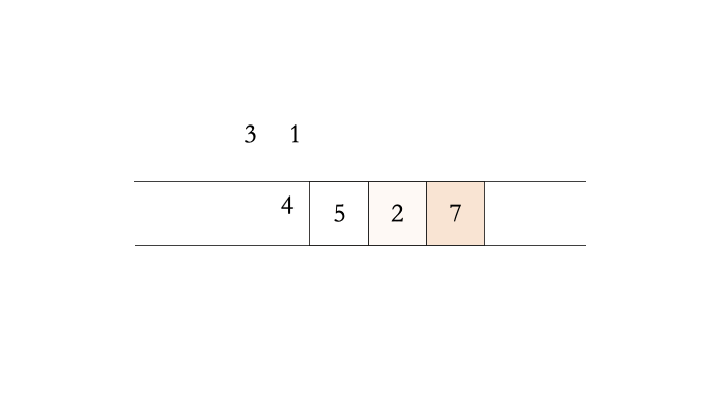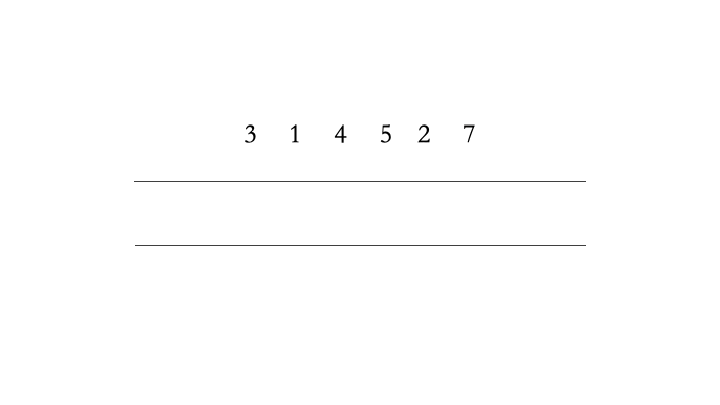
之前我们讲过”
队列的实现
和栈一样,它可以使用数组实现(顺序队列),也可以使用链表实现(链式队列)。
顺序队列
public class QueueArray<T>
{
//存储内容的泛型数组
public T[] items;
//数组长度
private int len;
//使用头指针和尾指针辅助入队、出队操作
int head, tail = 0;
public QueueArray(int capacity)
{
items = new T[capacity];
len = capacity;
}
//入队
public bool Enqueue(T val)
{
//尾指针与数组长度相同,说明队列已满,返回false(注意,该判断存在问题)
if (tail == len)
return false;
items[tail++] = val;
return true;
}
//出队
public T Dequeue()
{
if (tail == head)
throw new Exception("Queue is empty");
return items[head++];
}
}
现在基本功能已经实现了,但仔细分析会发现,代码中的tail和head都只会向后移动(数量只会增加),因此tail == len并不代表数组已满,因为数组头部的数据可能已经出队了,前面出现了许多空闲空间。如下图所示
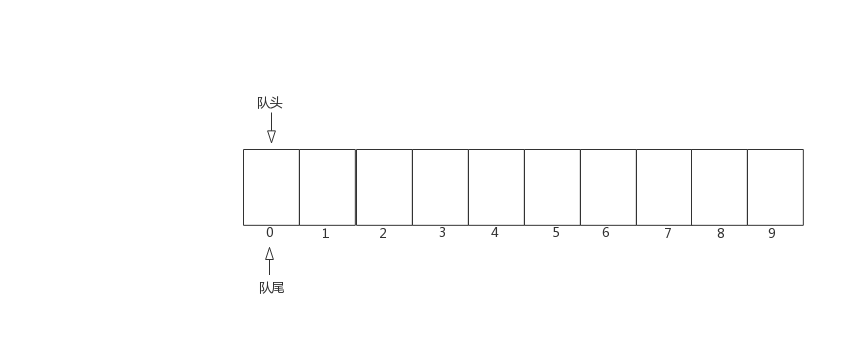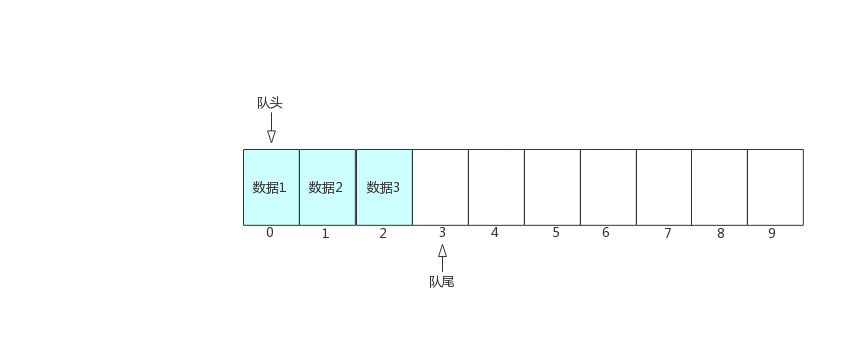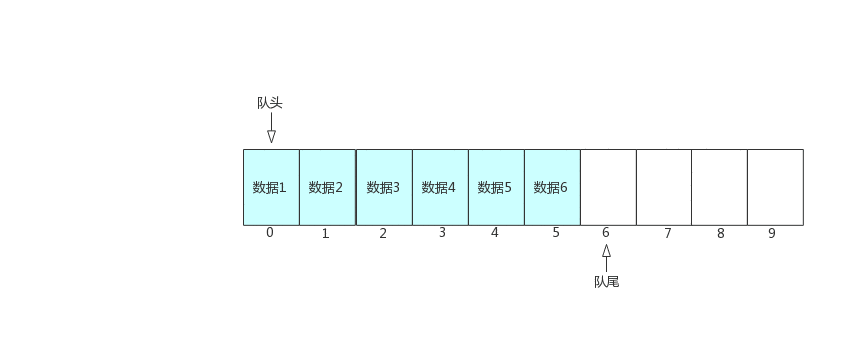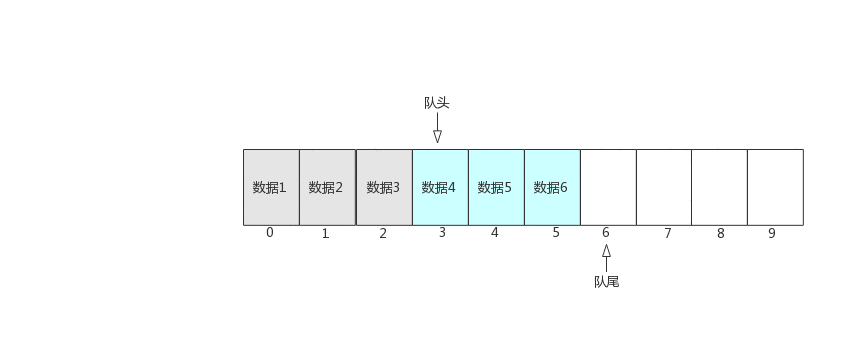
随着不停的执行入队、出队操作,即使数组中还有空闲空间,也无法继续往队列中添加数据了。此时,需要使用数据搬移,即将队列中的元素整体搬移到数组头,如下图所示。
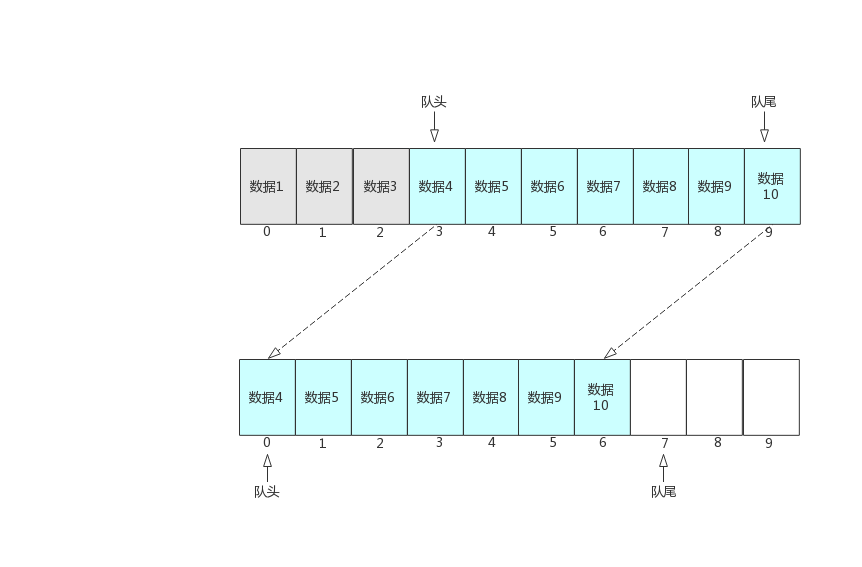
该操作只需要在入队并且”队列已满“的时候执行,因此我们需要修改Enqueue()的代码为
//入队
public bool Enqueue(T val)
{
if (tail == len)
{
// tail ==n && head==0,表示整个队列都占满了
if (head == 0) return false;
// 数据搬移
for (int i = head; i < tail; ++i)
{
items[i - head] = items[i];
}
// 搬移完之后重新更新head和tail
tail -= head;
}
items[tail++] = val;
return true;
}
循环队列
循环队列也是基于数组实现的,并且能够很好的解决上面当tail==n需要数据搬移的问题(数据搬移会消耗许多性能)。
顾名思义,环形队列长得像是一个环,怎么将数组“变成”环呢?思路是当tail==n时,如果有空闲位置让tail = (tail + 1) % len,即将尾部指针转移到数组头部来开始新的循环,这样修改最关键的就是要正确判断队空和队满的条件。下图中蓝色代表头指针,红色代表尾指针
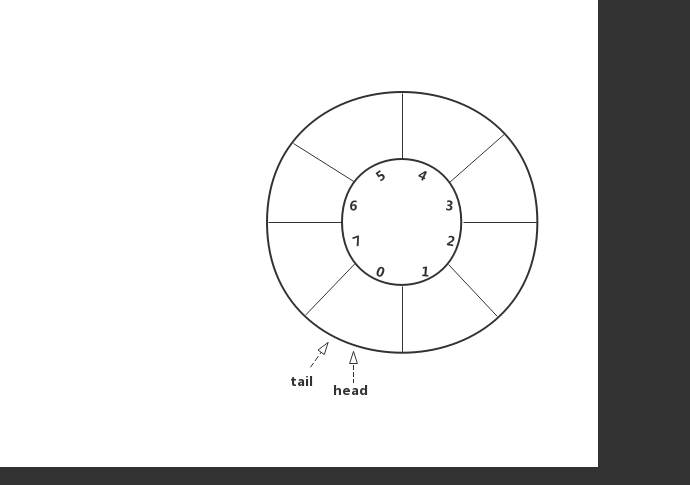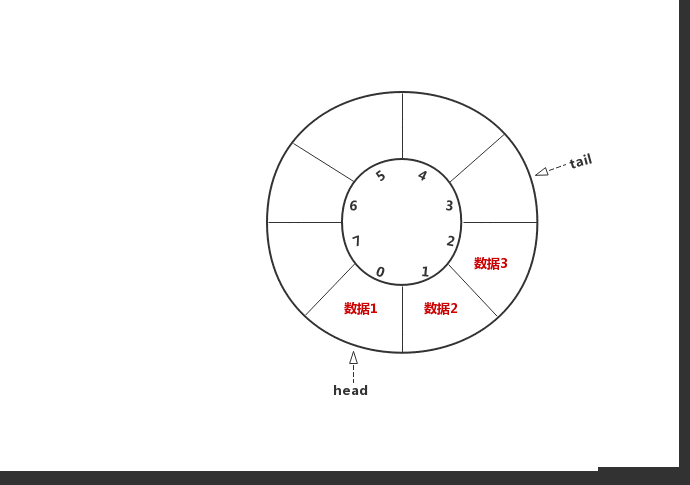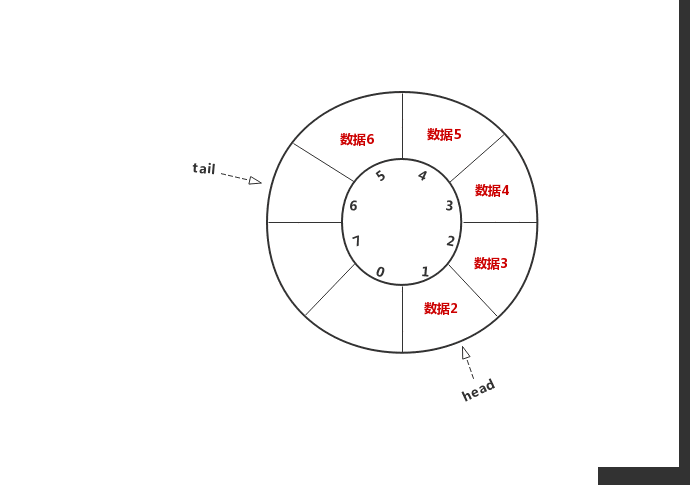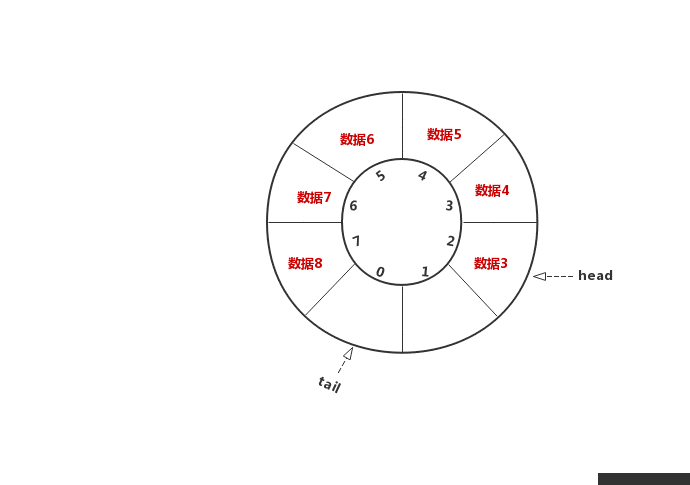
修改入队和出队的代码
//入队
public bool Enqueue(T val)
{
//使用尾指针与头指针来判断队列是否满
if ((tail + 1) % len == head)
return false;
items[tail] = val;
tail = (tail + 1) % len;
return true;
}
//出队
public T Dequeue()
{
if (tail == head)
throw new Exception("Queue is empty");
T ans = items[head];
head = (head + 1) % len;
return ans;
}
因为判断队满使用的是(tail+1)%n=head,所以当队列满时,tail指向的位置实际上是没有存储数据的,浪费了数组的一个存储空间。
💁♂ 代码虽然不多,但最好能够自己手动实现
链式队列
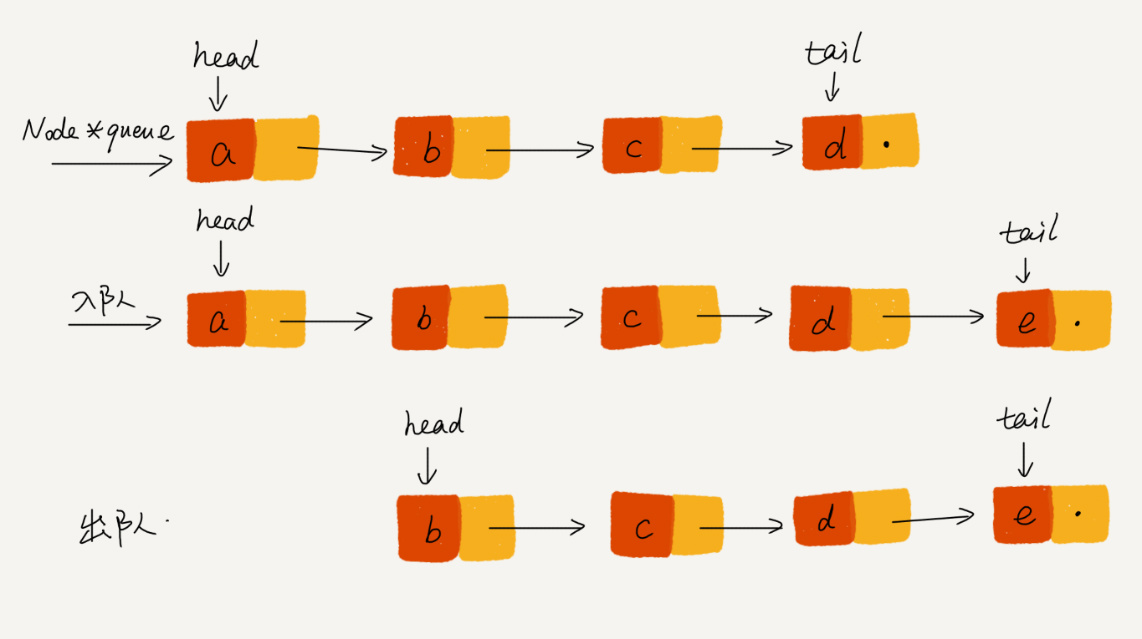
基于链表的实现,我们同样需要两个指针:head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。如图所示,入队时,tail->next= new_node, tail = tail->next;出队时,head = head->next,实现起来比较简单,这里就省略了🤗
总结