【推断统计】 1. 样本和总体 总体:目标事件的全体 样本:总体的一部分(总体的子集) 2. 推断统计: 用样本数据对总体进行归纳的统计过程 假定:样本对总体具有代表性 3. 假设检验: 两个假设:原假设+备择假设 原假设:表述为一个处理没有影响--(小概率事件)H0
备择假设:表述为该处理有影响 H1 4. 抽样误差: 样本和总体之间的差别(样本越少,样本和总体之间的差别越大) 5. P值 P值:表示原假设为真时得到特定结果(甚至更极端结果)的确切概率--“显著性” 作用:alpha(α)--0.05(0.01,0.1) 进行比较: 如果p值小于等于0.05(α),则拒绝原假设---“显著性”或者“统计意义上的显著性” 如果p值大于0.05(α),则不拒绝原假设(接受原假设)---“不显著”
一、T检验
单样本T检验、独立样本T检验、配对样本T检验 【单样本T检验】 将样本均值与总体均值或估计的总体均值进行比较 1. 目的:判断样本均值是否与总体均值或估计的总体均值是否有显著区别 2. 所需数据: 样本(来自总体)+ 因变量(连续) 3. 假设条件: a. 观测值独立 b. 总体当中的因变量服从正态分布 4. 原假设和备择假设: 原假设:H0: μ=μ0 备择假设:H1: μ≠μ0 μ表示样本均值,μ0表示总体均值 5. 假设检验: 假定原假设为真的情况下,如果T检验的结果看起来是不可能(p值小于等于0.05),则拒绝原假设; 如果T检验的结果看起来有可能(p值大于0.05),则不拒绝原假设
6. 具体步骤 a. 导入数据 b. 分析数据:分析--比较平均值--单样本T检验 注意:检验值里放总体样本均值,切记一定放 c. 解释输出的结果: 单样本统计:标准误差平均值=标准差/sqrt(个案数) 单样本检验:t=样本均值与总体均值之差/样本标准误差平均值=5.2/0.3507 自由度=个案数-1 d. 结论:某高校随机抽取600名大学生的平均体重(55.2kg)明显高于大学生的平均体重(50kg)
单样本T检验

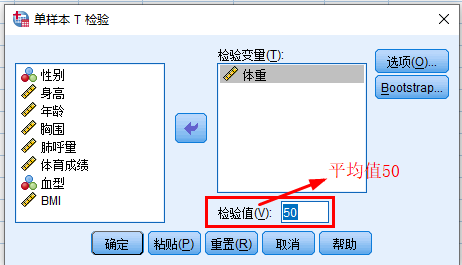
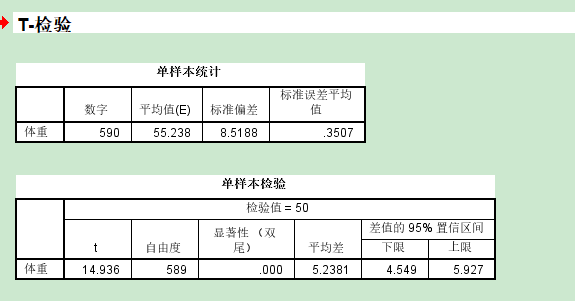
结论:某高校随机抽取600名大学生的平均体重(55.2kg)明显高于大学生的平均体重(50kg
练习一:
1 某药物在某种溶剂中溶解后的标准浓度为20.00mg/L。现测量该药物溶解11次,请分析该方法测量所得结果是否与标准浓度值有所不同?
溶液.sav
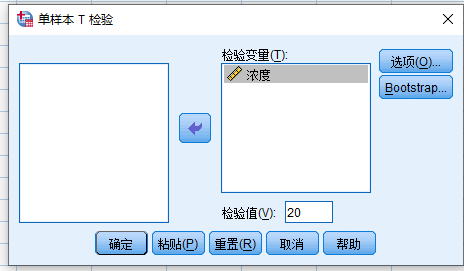
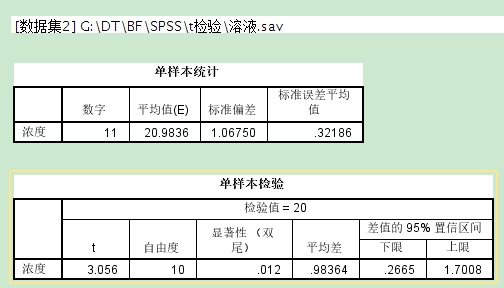
p=0.012<0.05拒绝原假设,接受备选假设:请分析该方法测量所得结果比标准浓度值大
独立样本T检验

案例描述:
现希望评价2007年4月第一次调查时不同性别人群的消费者信心指数是否存在差异。
数据: CCSS_Sample.sav
1. 目的:比较两组独立样本的平均值是否存在显著差异 2. 所需数据: 代表两个不同分组的自变量+连续因变量 3. 假设条件: a. 观测值独立 b. 各总体的因变量取值服从正态分布 c. 两总体方差相同--莱文检验 4. 原假设和备择假设: 原假设:H0: μ1=μ2 备择假设: H1:μ1≠μ2 μ1、μ2分别代表是两个样本的均值 5. 假设检验:*** 在原假设为真的情况下,如果t检验的结果看起来不可能(p值小于等于0.05),则拒绝原假设,说明两个样本均值不相同;
如果t检验结果有可能发生(p值大于0.05),则接受原假设,说明两个样本的均值相同的 6. 具体步骤: a. 导入数据 b. 分析数据:分组变量后面“??”表示定义组别分别对应的数字名称 c. 解释输出结果: 组统计: 独立样本检验:莱文方差检验(检验两总体的方差是否齐性--相同)+独立样本t检验 【莱文方差检验】 原假设:H0:σ1^2=σ2^2 备择假设:H1:σ1^2≠σ2^2 σ1^2、σ2^2分别代表两个总体的方差 判定:p≤0.05,拒绝原假设,方差不相同 p>0.05,接受原假设,方差相同 【独立样本t检验】 结论:两个样本的均值相同的 t=两样本均值之差/两样本标准误差差值=0.018/1.2314 d. 结论:2007年4月第一次调查时不同性别人群的消费者信心指数不存在差异,即相同

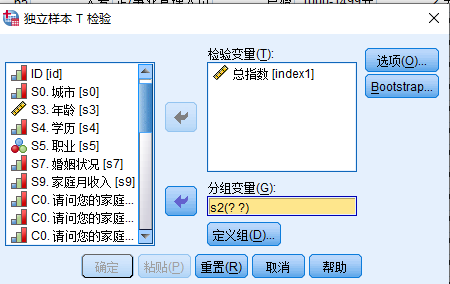
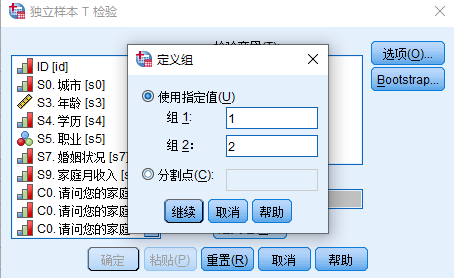
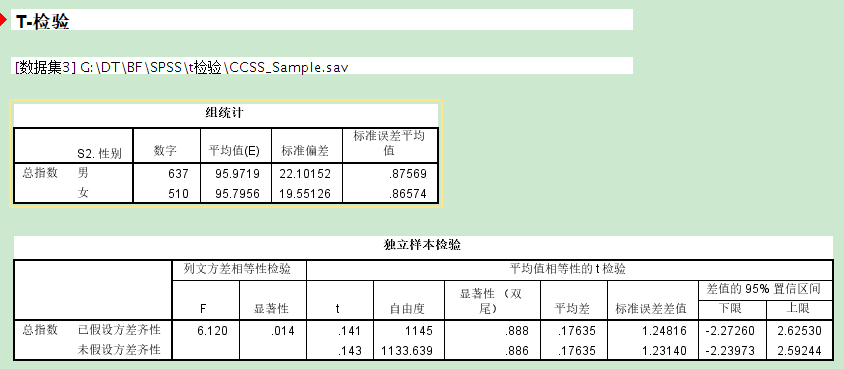
d. 结论:2007年4月第一次调查时不同性别人群的消费者信心指数不存在差异,即相同
练习题二:
2 希望评价两位老师的教学质量,试比较其分别任教的甲、乙两班考试后的成绩是否存在差异?
两班成绩.sav
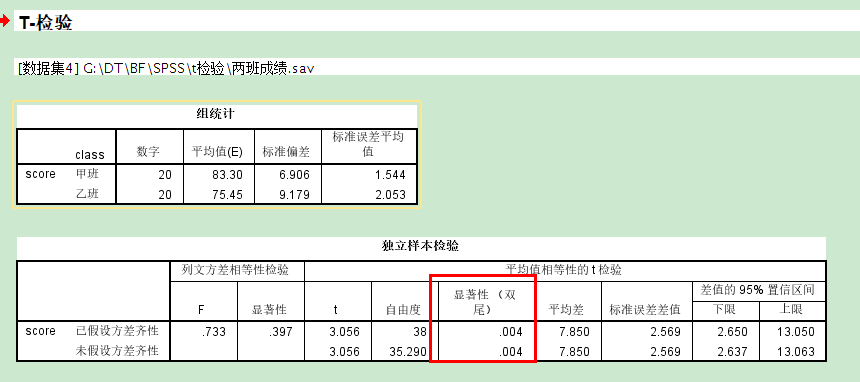
拒绝零假设,有统计显著,存在差异,甲班均值大于乙班
配对样本-T检验
1. 目的:检验两关联分组的因变量均值之间是否存在显著差异 2. 所需数据: 两关联分组或分类的自变量+连续因变量 3. 假设条件: a. 组内观测值独立 b. 两总体差值服从正态分布 4. 原假设和备择假设: 原假设:H0: μ1-μ2=0 备择假设:H1: μ1-μ2≠0 μ1、μ2分别代表是两个样本的均值
5. 假设检验: 在原假设为真的情况下,如果t检验的结果看起来不可能(p值小于等于0.05),则拒绝原假设,说明两个样本均值存在差异; 如果t检验结果有可能发生(p值大于0.05),则接受原假设,说明两个样本的均值没有差异
6. 具体步骤: a. 导入数据 b. 分析数据 c. 解释输出结果: 配对样本统计:治疗前的平均值明显大于治疗后的平均值,是否具有显著性? 配对样本相关性:对t检验不起关键作用,其中的相关性的值--Pearson相关系数 配对样本检验:t=样本之间的均值差/样本差值的标准误差平均值=10/3.78 d. 结论:病人治疗前的平均舒张压(122.1mmHg)高于治疗后的平均舒张压(112.1mmHg),说明药物具有降压效果

案例描述:
用某药治疗10名高血压病人,对每一病人治疗前、后的舒张压(mmHg)进行了测量,结果如下,问该药有无降压作用?
数据:降压效果分析.sav
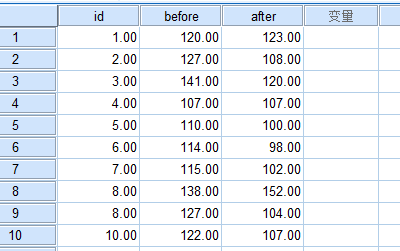
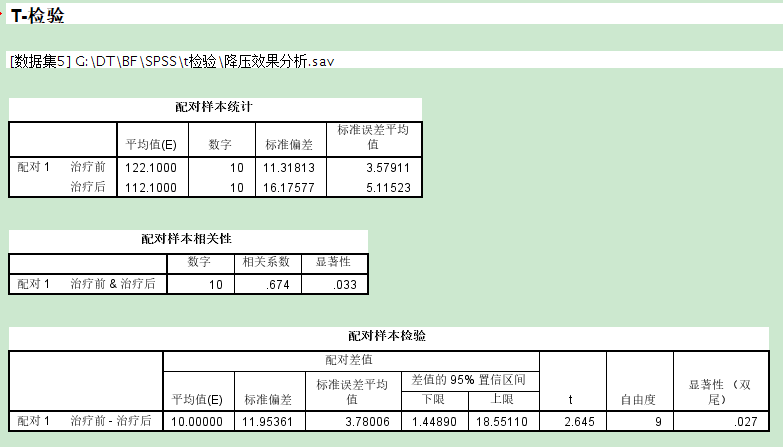
该药有降压作用
练习三:
测量结果,试问干预前后该地区贫血儿童血红蛋白平均水平有无变化?
血红蛋白.sav
1111
悟已往之不谏,知来者之可追。

