假设检验时数据分析必须学习的方法
第一部分:误差思维和置信区间
什么是误差思维?
误差永远存在、不可避免随机干扰因素的影响
一个量在测量、计算或观察过程中由于某些错误或通常由于某些不可控制的因素的影响而造成的变化偏离标准值或规定值的数量 ,误差是不可避免的。
只要有估计,就会有误差。
什么是置信区间?
置信区间:误差范围
什么是置信水平?
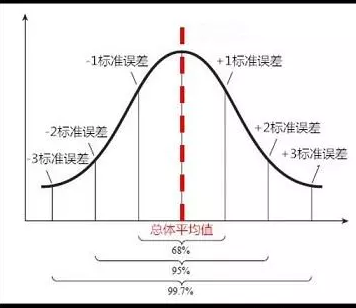
置信水平:区间包含总体平均值的概率p(a<样本平均值<b)=Y%
这里选常用置信水平%95,即精度为2个标准误差范围内:


通过游戏可视化理解置信区间?
如何计算大样本的置信区间?
大样本:当一个抽样调查的样本数量大于30。
这时候可以近似看出样本抽样分布趋近于正态分布,因此它符合中心极限定理。
下面以计算全国成年男性的平均身高为例,假设抽取样本100人,平均值167.1cm,标准差0.2cm
1.确定要求解的问题
计算全国成年男性的平均身高范围及精度
2.求样本的平均值和标准误差

3.确定置信水平
这里选常用置信水平%95,即精度为2个标准误差范围内:
4.求出置信区间上下限的值
(1)由于选用的样本大小为100大于30符合正态分布,先求出如下图中两块红色区域面积(概率):
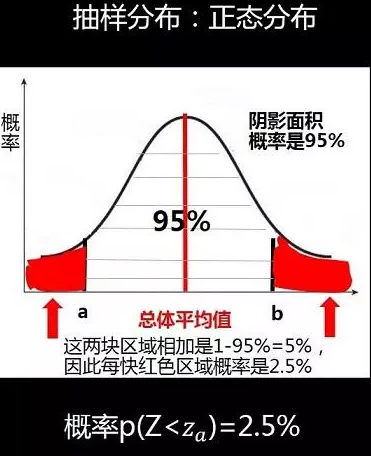
(2)通过查z表格查出标准分Z=-1.96

(3)求出a和b的值的方法:
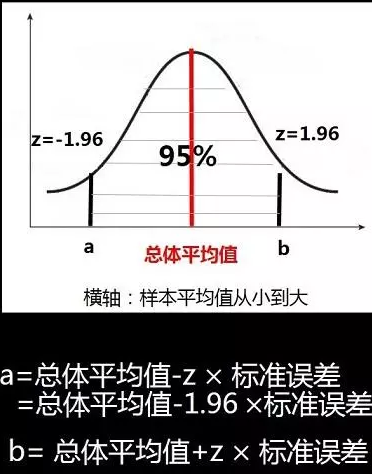
(4)根据中心极限定理,样本平均值约等于总体平均值,最终求出a和b的值:
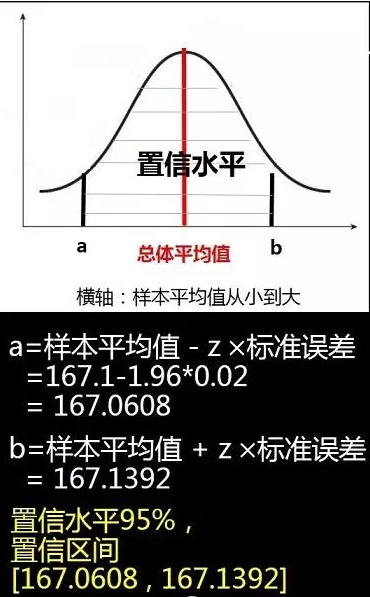
结论:当我们选用置信水平为%95时,求得置信区间为[167.0608,167.1392],
即在两个标准误差范围内,全国成年男性的平均身高为167.0608cm到167.1392cm之间。
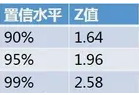
5.常用置信水平及其对应Z值(标准分)
如何计算小样本的置信区间?
小样本:当一个抽样调查的样本数量小于30。
这时候抽样分布符合t分布:
在概率论和统计学中,t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。
如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
这时候抽样分布符合t分布:
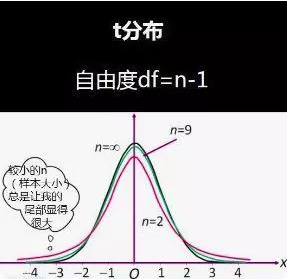
自由度:是指在不影响给定限制条件的情况下,可以自由变换信息的数量。可以将自由度看做估算其他信息时可有的独立信息数量。
在计算自由度的公式中n表示样本数量。
下面是以医院的药物分析为例,已知某种新药物A,现在选取10只小白鼠作为样本注射药物A,对其进行神经刺激并记录反应时间。
经过实验发现平均反应时间为1.05秒,样本标准差为0.5秒。
1.确定要求解的问题
新药物A对神经的反应时间范围
2.求样本的平均值和标准误差
药物A标准误差为:
药物A标准误差为:

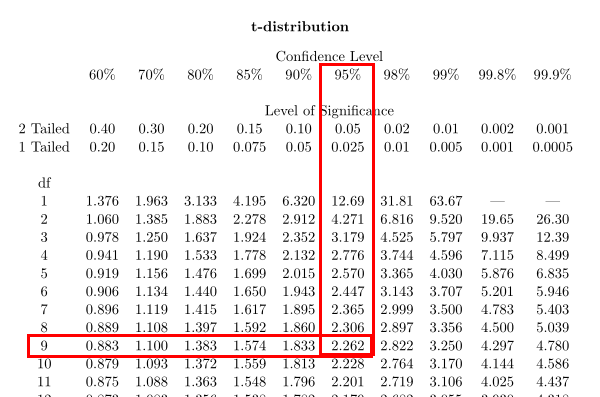
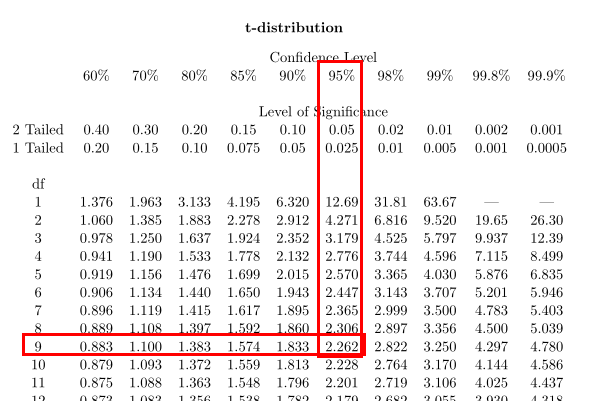
3.查找t表格,求t值
计算自由度:df = n-1 = 10 - 1 = 9
这里依然选用置信水平%95,双侧和单侧表示的是t分布中的面积。
根据自由度df和置信水平查找t表格,求t值:

4.求出置信区间上下限的值
根据上面查表求得t = 2.262,代入下面的公式,求出置信区间上下限a、b的值:
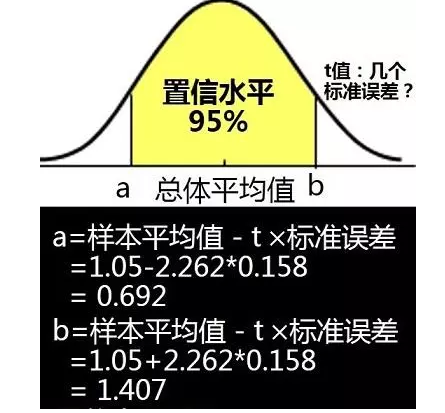
结论:当我们选用置信水平为%95时,求得置信区间为[0.692,1.407],即在两个标准误差范围内,新药物A对神经的反应时间为0.692秒到1.407秒之间。

python的科学计算包scipy如何使用?
第二部分:假设检验
什么是批判性思维?
一种人对生活中的信息理性分析和判断的能力
什么是假设检验?
假设检验(hypothesis testing),又称统计假设检验,是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。
显著性检验是假设检验中最常用的一种方法,也是一种最基本的统计推断形式,其基本原理是先对总体的特征做出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受做出推断。
常用的假设检验方法有Z检验、t检验、卡方检验、F检验等。
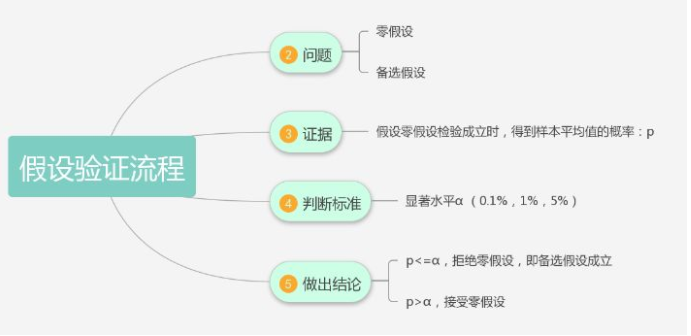
假设检验的套路:
(1)问题是什么
(2)证据是什么
(3)判断标准是什么
(4)做出结论

单样本检验:#案例超级引擎
因为这里只有1个样本,所以选择单样本检验
一、描述统计分析
我们开展调查研究并计算统计结果时,我们会在报告的第一部分进行描述统计分析,例如平均值和标准差。描述统计量是研究的核心。告诉我们研究中发生的情况,应该始终报告出来。
#导入包 import pandas as pd import numpy as np import matplotlib.pyplot as plt #样本数据集 dataSer=pd.Series([15.6,16.2,22.5,20.5,16.4, 19.4,16.6,17.9,12.7,13.9]) #样本平均值 sample_mean=dataSer.mean() ''' 这里要区别:数据集的标准差,和样本标准差 数据集的标准差公式除以的是n,样本标准差公式除以的是n-1。 样本标准差,用途是用样本标准差估计出总体标准差 pandas计算的标准差,默认除以的是n-1,也就是计算出的是样本标准差 pandas标准差官网地址:https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.std.html ''' #样本标准差 sample_std=dataSer.std() print('样本平均值=',sample_mean,'单位:ppm') print('样本标准差=',sample_std,'单位:ppm')
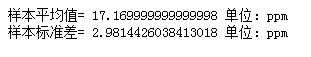
二、推论统计分析 推论统计分析报告中包括:假设检验,置信区间,效应量 1. 问题是什么? 零假设和备选假设 要研究的问题是:这些样本数据是否满足新标准呢? 根据这个问题我提出来下面两个互为相反的假设。 零假设H0:公司引擎排放不满足标准,也就是平均值u>=20。这里的20是政府规定新标准的最低可能值。 零假设总是表述为研究没有改变,没有效果,不起作用等,这里就是不满足标准。 备选假设H1:公司引擎排放满足标准,也就是平均值u<20
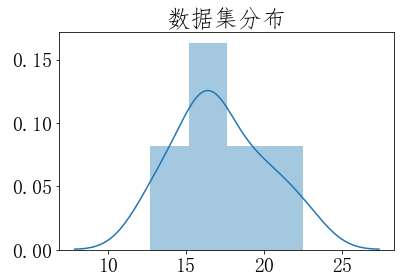
检验类型 检验类型有很多种,因为这里只有1个样本,所以选择单样本检验。 检验类型参考资料:http://support.minitab.com/zh-cn/minitab/17/topic-library/basic-statistics-and-graphs/hypothesis-tests/tests-of-means/types-of-t-tests/ 抽样分布类型 我们还要判断抽样分布是哪种?因为抽样分布的类型,决定了后面计算p值的不同。 在我们这个汽车引擎案例中,样本大小是10(小于30),属于小样本。那小样本的抽样分布是否满足t分布呢?因为t分布还要求数据集近似正态分布,所以下面图片我们看下样本数据集的分布长什么样。
"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码 ''' 直方图能够粗略估计数据密度,如果想给数据一个更精确的拟合曲线(专业术语叫:核密度估计kernel density estimate (KDE)), Seaborn 可以很方便的画出直方图和拟合曲线。 查看数据集分布官网教程地址:https://seaborn.pydata.org/tutorial/distributions.html ''' ''' 需要在conda中先安装绘图包seaborn: conda install seaborn ''' import seaborn as sns #查看数据集分布 sns.distplot(dataSer) plt.title('数据集分布') plt.show()
seaborn中的distplot主要功能是绘制单变量的直方图
通过观察上面数据集分布图,数据集近似正态分布,满足t分布的使用条件,所以抽样分布是t分布,自由度df=n-1=10-1=9。
检验方向 单尾检验(左尾,右尾),还是双尾检验? 因为备选假设是公司引擎排放满足标准,也就是平均值u<20 所以我们使用单尾检验中的左尾检验 总结 综合以上分析,本次假设检验是单样本t检验,单尾检验中的左尾。
2.证据是什么?
在零假设成立前提下,得到样本平均值的概率p是多少? 计算p值步骤也很简单: 1)计算出标准误差 标准误差=样本标准差除以样本大小n的开方。这里的样本标准差是用来估计总体标准差的 2)计算t值 t=(样本平均值-总体平均值)/标准误差 3)根据t值,自由的计算出概率p值
''' 方法二:用python统计包scipy自动计算 用scipy计算出的是:双尾检验 单(1samp)样本t检验(ttest_1samp):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_1samp.html 相关(related)样本t检验(ttest_rel):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_rel.html 双独立(independent)样本t检验(ttest_ind):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html ''' #导入统计模块(stats) from scipy import stats #总体平均值 pop_mean=20 ''' ttest_1samp:单独样本t检验 返回的第1个值t是假设检验计算出的(t值), 第2个值p是双尾检验的p值 ''' t,p_two =stats.ttest_1samp(dataSer,pop_mean) print('t值=',t,'双尾检验的p值=',p_two)

''' 因为scipy计算出的是双尾检验的t值和p值,但是我们这里是左尾检验。 根据对称性,双尾的p值是对应单尾p值的2倍 ''' #单尾检验的p值 p_one=p_two/2 print('单尾检验的p值=',p_one)

3. 判断标准是什么?
#判断标准(显著水平)使用alpha=5% alpha=0.05
4. 做出结论
''' 左尾判断条件:t < 0 and p_one < 判断标准(显著水平)alpha 右尾判断条件:t > 0 and p_one < 判断标准(显著水平)alpha ''' #做出结论 if(t<0 and p_one< alpha): #左尾判断条件 print('拒绝零假设,有统计显著,也就是汽车引擎排放满足标准') else: print('接受零假设,没有统计显著,也就是汽车引擎排放不满足标准')

(5)置信区间
''' 1)置信水平对应的t值(t_ci) 查t表格可以得到,95%的置信水平,自由度是n-1对应的t值
10-1=9 2)计算上下限 置信区间上限a=样本平均值 - t_ci ×标准误差 置信区间下限b=样本平均值 - t_ci ×标准误差 ''' ''' 查找t表格获取95%的置信水平,自由度是n-1对应的t值 ''' t_ci=2.262
#使用scipy计算标准误差 se=stats.sem(dataSer) #置信区间上限 a=sample_mean - t_ci * se #置信区间下限
print('单个平均值的置信区间,95置信水平 CI=(%f,%f)' % (a,b))

6.效应量
还需要在报告中给出效应量(effect size)。什么是效应量呢? 效应量是指处理效应的大小,例如药物A比药物B效果显著。度量效应量有很多种,但大多数都属于两大主要类别。 1)第一种叫做差异度量 例如在对比平均值时,衡量效应大小的常见标准之一是Cohen's d Cohen's d = (样本平均值1-样本平均值2) / 标准差 Cohen's d 除以的是标准差,也就是以标准差为单位,样本平均值和总体平均值之间相差多少。 2)第二种叫做相关度度量 例如R平方,表示某个变量的变化比例与另一变量的关系。可以用t检验的信息推出R平方的公式,这里的t值从t检验中获得的值,df是自由度。 r2=t2 / (t2+df),其中r2是指r的平方,t2是t的平方 如果r平方等于20%,表示我们可以说通过知道另一个变量能够接受相关变量20%的变化情况 为什么要给出效应量? 在判断某个调查研究的结果,是否有意义或者重要时,要考虑的另一项指标是效应量。效应量太小,意味着处理即使达到了显著水平,也缺乏实用价值。 所以,在假设检验中,我们给出了是否具有统计显著性,也要给出效应量,一起来判断研究结果是否有意义。 效应量报告格式:d=x.xx ,R2=.xx
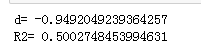
''' 效应量:差异指标Cohen's d ''' d=(sample_mean - pop_mean) / sample_std ''' 效应量:相关度指标R2 ''' #样本大小 n=10 #自由度 df=n-1 R2=(t*t)/(t*t+df) print('d=',d) print('R2=',R2)
三、数据分析报告
1、描述统计分析 样本平均值17.17ppm,样本标准差2.98ppm 2、推论统计分析 1)假设检验 独立样本t(9)=-3.00,p=.0074(α=5%),单尾检验(左尾) 公司引擎排放满足标准 2)置信区间 平均值的置信区间,95% CI=(17.11,17.23) 3)效应量 d=-0.94
置信区间APA格式:置信区间类型,置信水平CI=(a,b)
完成假设检验的套路是什么?如何用Python进行假设检验?
如何写推论统计学报告?