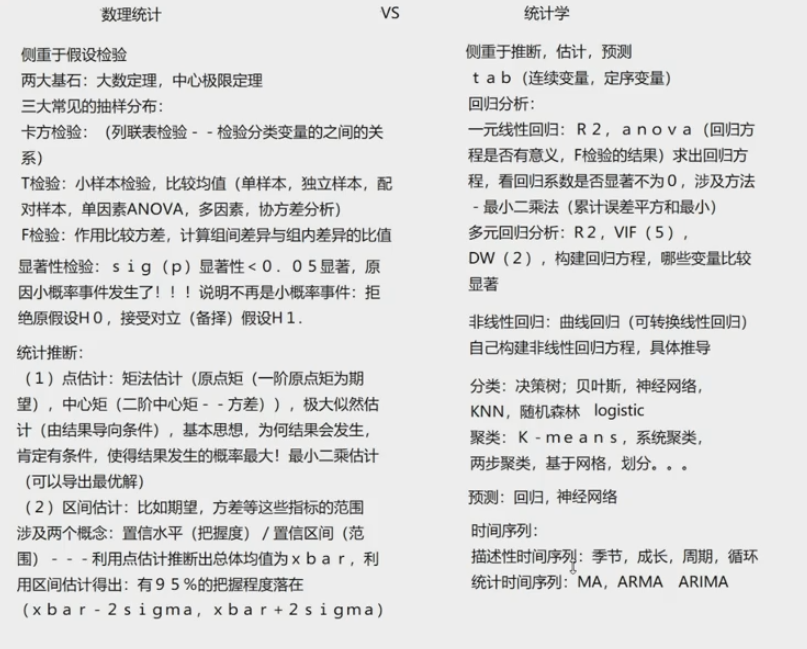


排列数:

组合数:

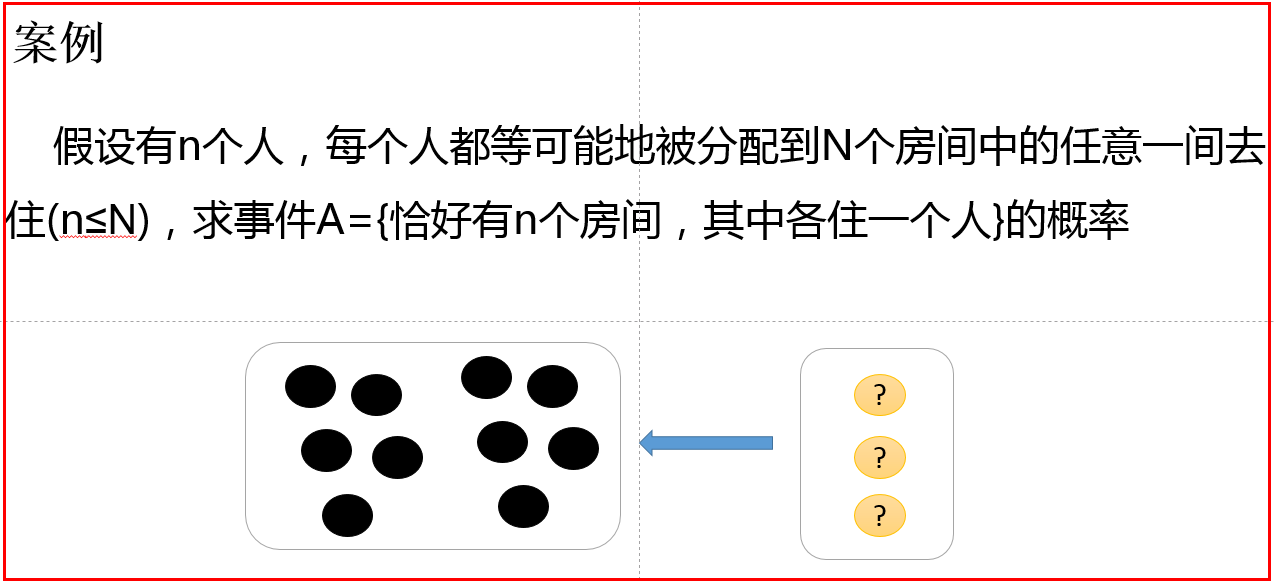


关联规则:
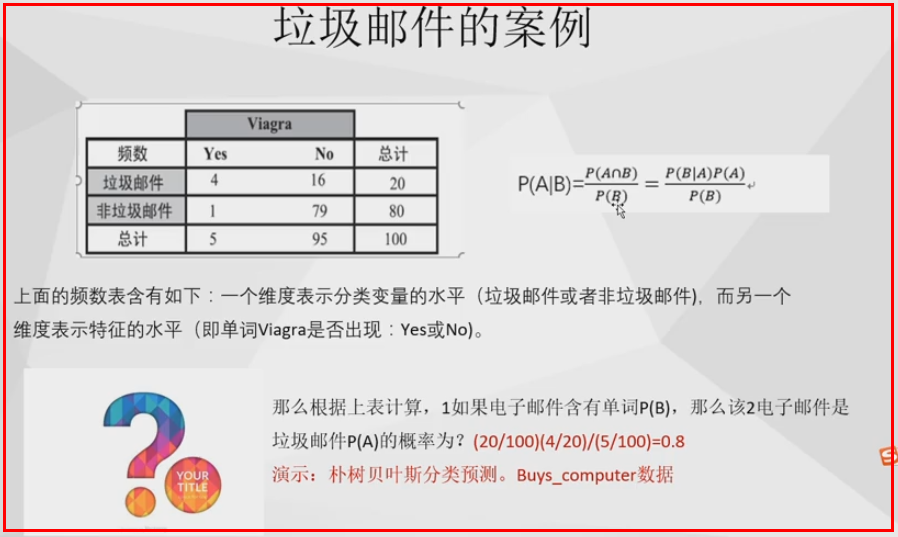
1、联合概率和条件概率
联合概率:P(AB)两个概率同时发生的概率



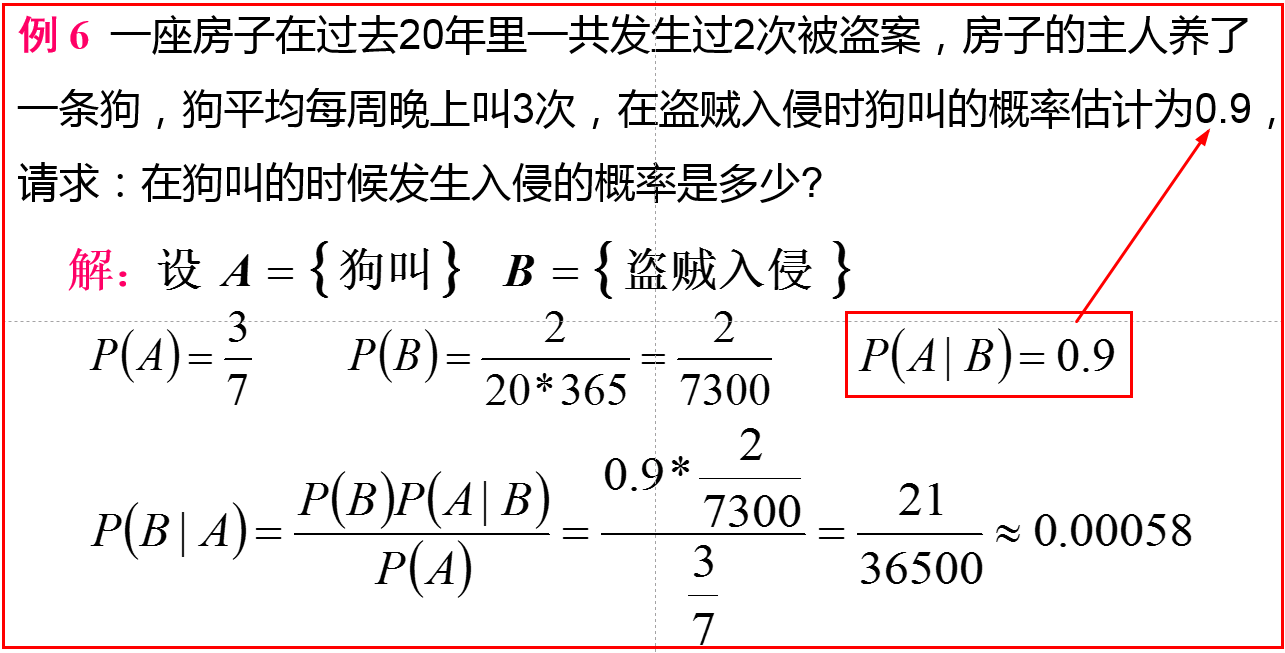
2、关联规则算法



这个发现为商家带来了大量的利润,但是如何从浩如烟海却又杂乱无章的大数据中,发现啤酒和尿布销售之间的联系呢?这又给了我们什么样的启示呢?
关联规则分析
关联规则挖掘的一个典型例子是购物篮分析。关联规则研究有助于发现交易数据库中不同商品(项)之间的联系,
找出顾客购买行为模式,如购买了某一商品对购买其他商品的影响。分析结果可以应用于商品货架布局、货存安排以及根据购买模式对用户进行分类。
3、全概率公式
条件概率、全概率=贝叶斯公式
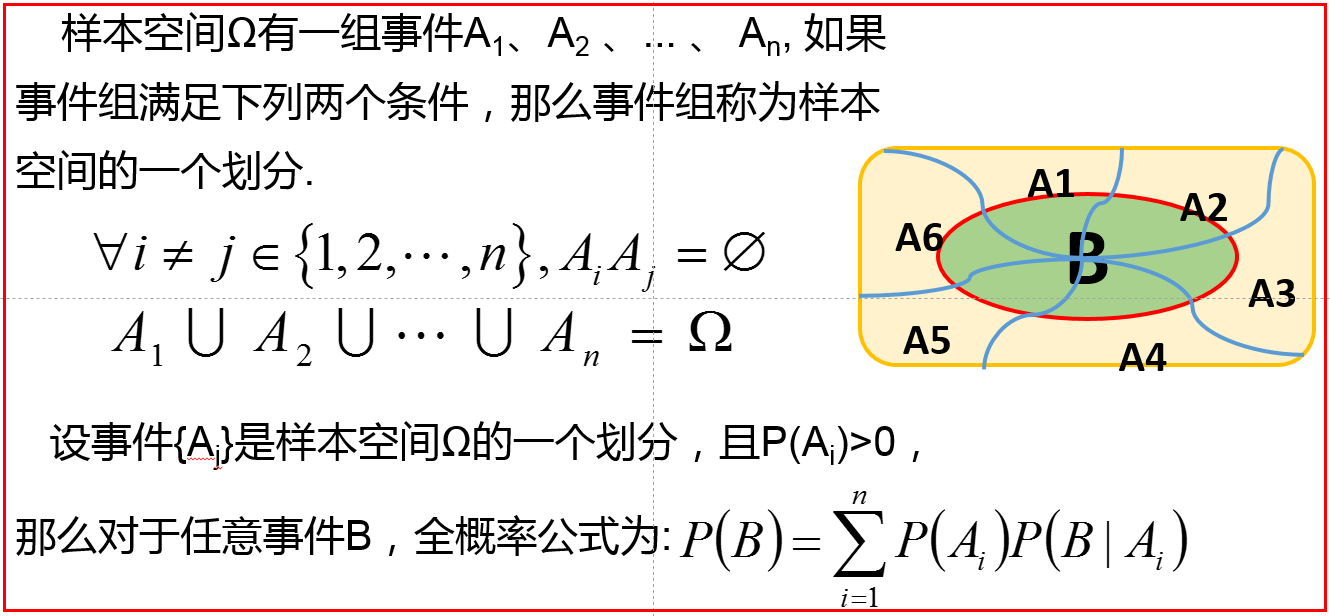

4、贝叶斯公式


P(B)=3/5 * 2/4 + 2/5 * 3/4 =3/5
2/4=P(B|A) 在A发生的条件下B发生 (先因后果)
P(A/B)在B发生的条件下B发生 (先果后因)
贝叶斯公式及例题
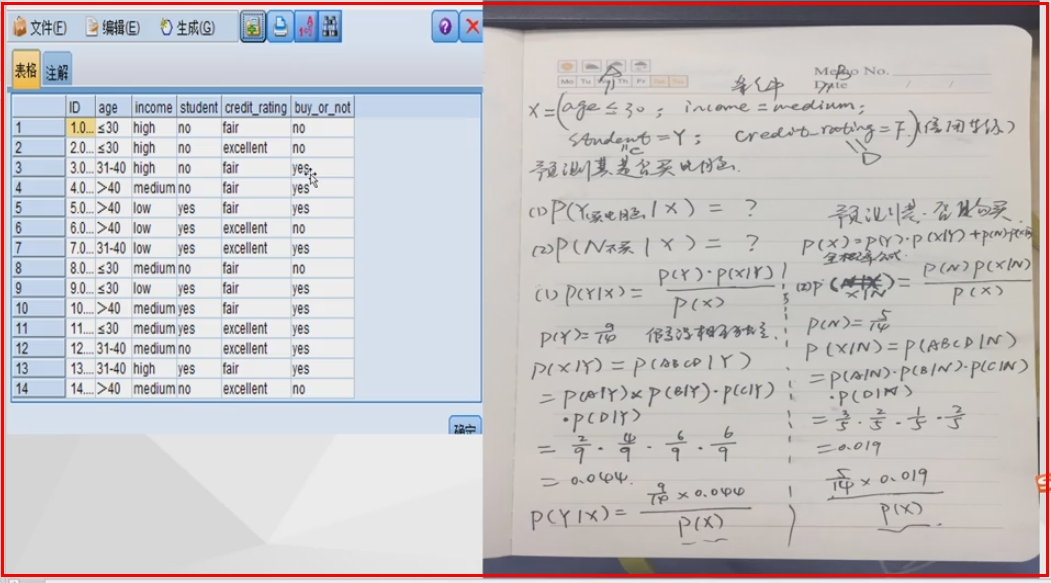
14个数据,Y:9个买,X:5个不买
A对应age
B对应 学student
判断是否为学生预测购买的概率
三、一维随机变量及其分布
数据的分散情况,分布在各未知的概率


区间的每个值都可以取到-----连续
只能取区间的部分点------离散
3.1离散型随机变量及其分布

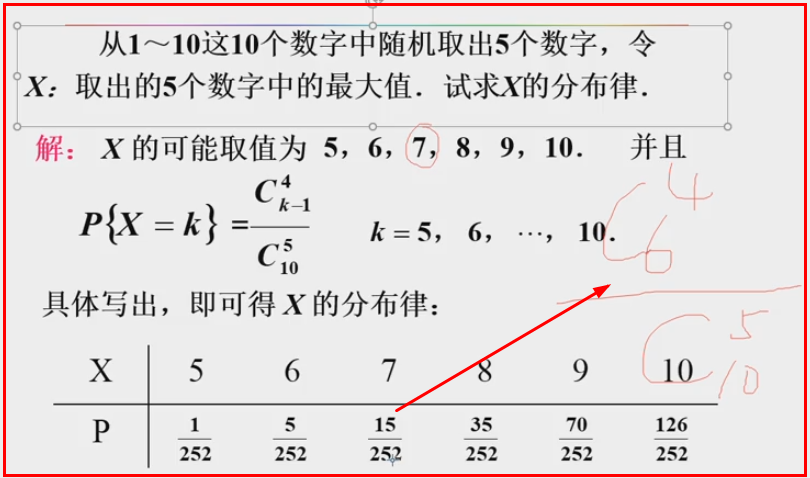
Bernoulli分布



Poisson分布--
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。


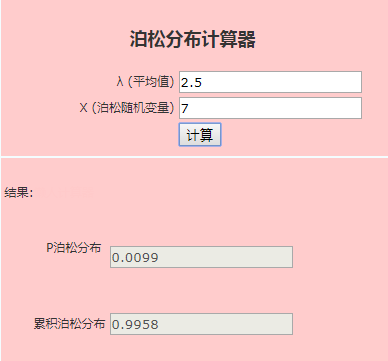


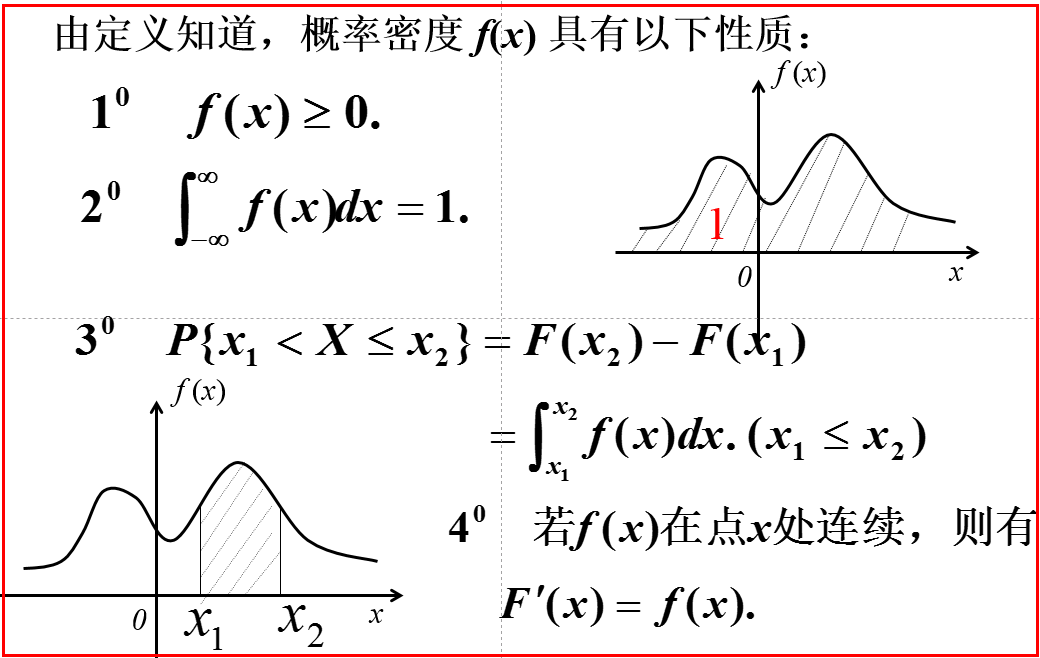
四、连续型随机变量及其概率密度


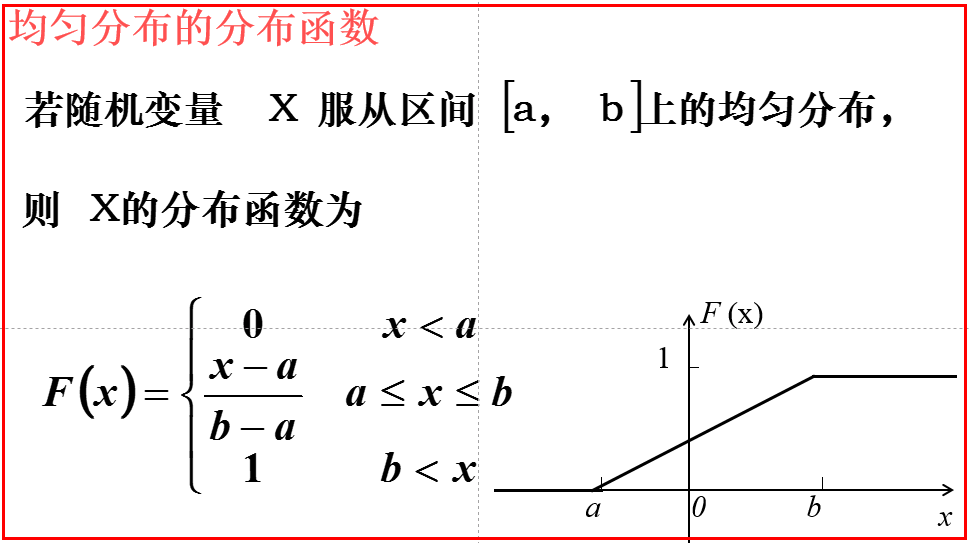
均匀分布

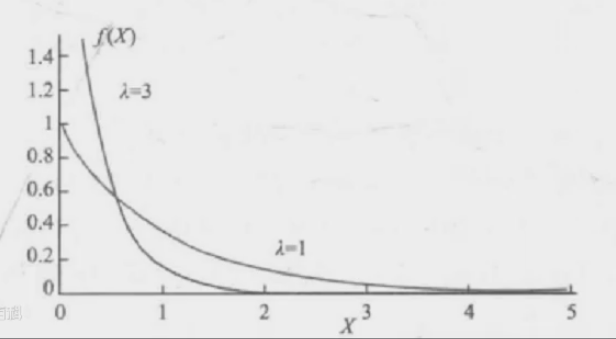
指数分布
指数分布公式的含义是什么?

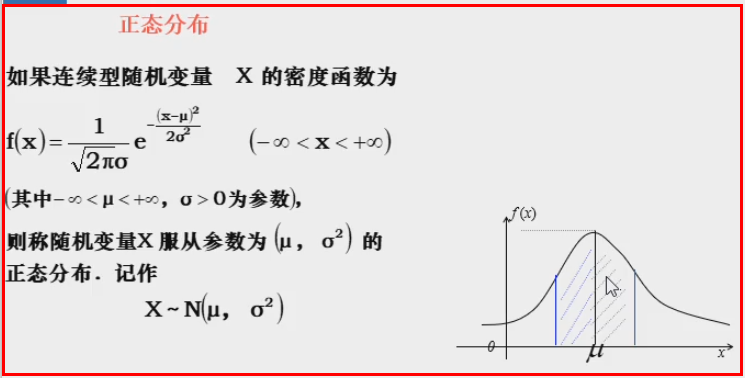
正态分布

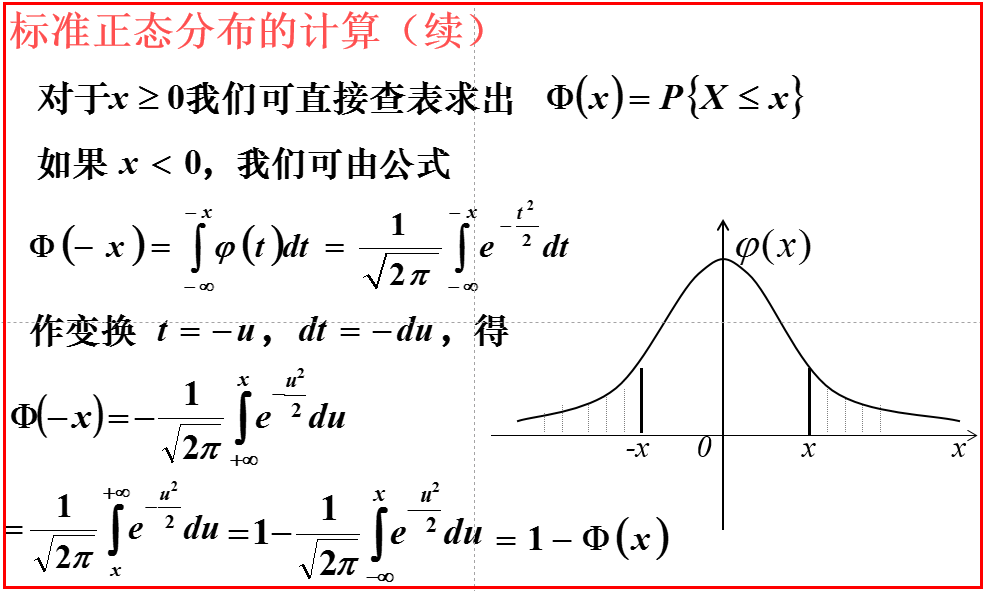
标准正态分布:
期望值μ=0,即曲线图象对称轴为Y轴,标准差σ=1条件下的正态分布,记为N(0,1)。


用软件处理小批量数据 例如500M的SPSS ,电脑就带不动,必须用代码Python
spss侧重于假设和检验
python侧重于大数据的 统计推断
泊松分布表示的是事件发生的次数,“次数”这个是离散变量,所以泊松分布是离散随机变量的分布。
指数分布是两件事情发生的平均间隔时间,“时间”是连续变量,所以指数分布是一种连续随机变量的分布。
可以用等公交车作为例子:
某个公交站台一个小时内出现了的公交车的数量 就用泊松分布来表示
某个公交站台任意两辆公交车出现的间隔时间 就用指数分布来表示

P(X<2)-P(X<1)
最小二乘法
做预测,做回归
最小二乘法,所谓“二乘”就是平方的意思

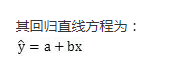
极大似然方法
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!
换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。
五、数值特征
5.1数学期望

体现数据的集中性
5.2 方差
体现数据的波动情况、越大说明波动越大




如何通俗地理解协方差和相关系数?
协方差代表了两个变量之间的是否同时偏离均值。


5.3 大数定律和中心极限定理
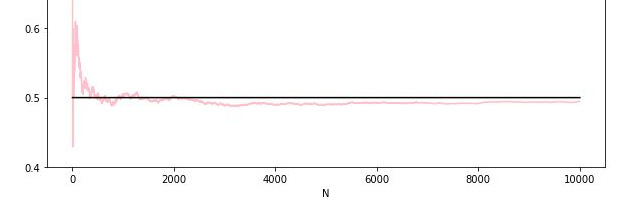
大数定律:当次数足够多可以用频率代替概率

简单而言,大数定律讲的是样本均值收敛到总体均值(就是期望)
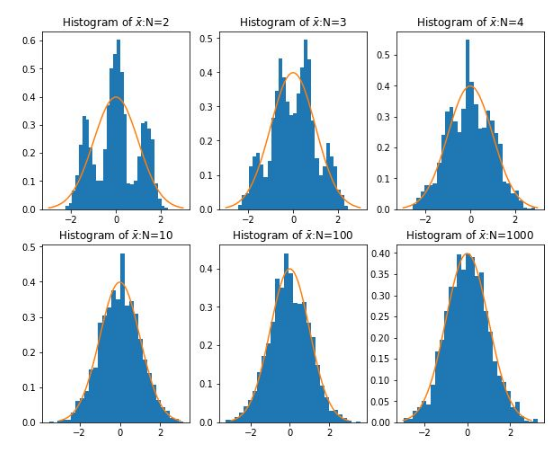
中心极限定律
而中心极限定理告诉我们,当样本量足够大时,样本均值的分布慢慢变成正态分布,就像这个图:
抽样分布
抽样分布就是统计量的分布,其特点是不包含未知参数且尽可能多的概括了样本信息。
除了常见的正态分布之外,还有卡方分布、t分布和F分布为最常见的描述抽样分布的分布函数。
这几个分布函数在数理统计中也非常有名。我们常说的卡方检验、t检验和F检验就跟这三个分布有关。
下面分别从定义、性质、函数图像和分位数等方面介绍三大分布。
悟已往之不谏,知来者之可追。

