数据结构

一、数据结构介绍

二、列表结构

 

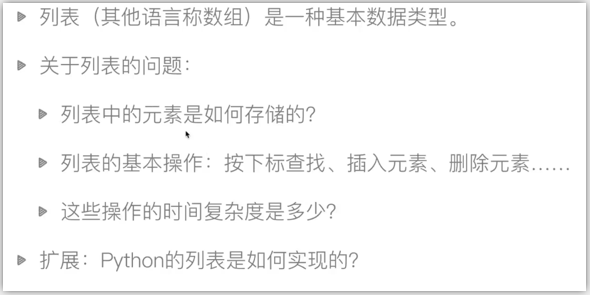
数组与列表两点不同：

　　1、数组元素类型要相同

　　2、数组长度固定(定义好就不变了)

列表里面存的是地址

列表可以增删

三、栈的结构----先进后出

递归的数据结构就是栈

 

取栈顶，只是确定值，不是取出来

class Stack:
    def __init__(self):
        self.stack = []
    def push(self,element):
        self.stack.append(element)
    def pop(self):
        # pop() 函数用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值。
        return self.stack.pop()
    def get_top(self):
        if len(self.stack)>0:
            return self.stack[-1]
        else:
            return None
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop())
print(stack.__dict__)

3
{'stack': [1, 2]}

栈的应用：

括号匹配问题

class Stack:
    def __init__(self):
        self.stack = []
    def push(self,element):
        self.stack.append(element)
    def pop(self):
        # pop() 函数用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值。
        return self.stack.pop()
    def get_top(self):
        if len(self.stack)>0:
            return self.stack[-1]
        else:
            return None

    def is_empty(self):
        return len(self.stack)==0


def brace_match(s):
    math = {'}':'{',']':'[',')':'('}
    stack = Stack()
    for ch in s:
        if ch in {'(','[','{'}:
            stack.push(ch)
        else:
            if stack.is_empty():
                return False
            elif stack.get_top()==math[ch]:
                stack.pop()
            else:
                return False
    if stack.is_empty():
        return True
    else:
        return False
print(brace_match('[{()}{}]'))

队列的介绍----先进先出

front 英 /frʌnt/ 美 /frʌnt/  前

rear 英 /rɪə/ 美 /rɪr/        后

 

 环形队列

class Queue:
    def __init__(self,size=100):
        self.queue = [0 for _ in range(size)]
        self.size = size
        self.rear = 0 # 队尾
        self.front = 0 # 队首

    def push(self,element):
        if not self.is_filled():
            self.rear = (self.rear+1) % self.size
            self.queue[self.rear] = element
        else:
            raise IndexError('Queue is filled')
    def pop(self):
        if not self.is_empty():
            self.front = (self.front+1) %self.size
            return self.queue[self.front]
        else:
            raise IndexError('Queue is empty')
    # 判断队空
    def is_empty(self):
        return self.rear==self.front

    # 判断队满
    def is_filled(self):
        return (self.rear+1)%self.size==self.front

q = Queue(5)
for i in range(4):
    q.push(i)
print(q.pop())
q.push(5)

队列的内置模块

　　双向队列

from collections import deque
# deque([iterable[, maxlen]]) --> deque object
q = deque([1,2,3,4,5],5)
q.append(6) # 队尾进队
print(q.popleft()) # 队首出队

# 用于双向队列
# q.appendleft(1) # 队首进队
# q.pop()

栈和队列的应用：迷宫问题

栈---深度优先(一条道走到黑)

maze 英 /meɪz/ 美 /mez/  迷宫

maze = [
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

dirs = [
    lambda x,y: (x+1,y),
    lambda x,y: (x-1,y),
    lambda x,y: (x,y-1),
    lambda x,y: (x,y+1)
]
# 起点：(x1,y1)；终点：(x2,y2)
def maze_path(x1,y1,x2,y2):
    stack = []
    stack.append((x1, y1))
    while(len(stack)>0):
        curNode = stack[-1] # 当前的节点
        if curNode[0] == x2 and curNode[1] == y2:
            # 走到终点了
            for p in stack:
                print(p)
            return True

        # x,y 四个方向 x-1,y; x+1,y; x,y-1; x,y+1
        # 得出结论：for 循环正常执行结束后，else 语句里面的内容也会正常执行。
        for dir in dirs:
            nextNode = dir(curNode[0], curNode[1])
            # 如果下一个节点能走
            if maze[nextNode[0]][nextNode[1]] == 0:
                stack.append(nextNode)
                # 已经走过的标记一下
                maze[nextNode[0]][nextNode[1]] = 2 # 2表示为已经走过
                break
        else:
            maze[nextNode[0]][nextNode[1]] = 2
            stack.pop()
    else:
        print("没有路")
        return False
# (1,1)为0  (8,8)为0 -对角线
maze_path(1,1,8,8)

 

使用队列解决迷宫问题

队列----广度优先

先到的排序时间最短

from collections import deque

maze = [
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

dirs = [
    lambda x, y: (x + 1, y),
    lambda x, y: (x - 1, y),
    lambda x, y: (x, y - 1),
    lambda x, y: (x, y + 1)
]


def print_r(path):
    curNode = path[-1]

    realpath = []

    while curNode[2] == -1:
        realpath.append(curNode[0:2])
        curNode = path[curNode[2]]

    realpath.append(curNode[0:2])  # 起点
    realpath.reverse()
    for node in realpath:
        print(node)


def maze_path_queue(x1, y1, x2, y2):
    queue = deque()
    queue.append((x1, y1, -1))
    path = []
    while len(queue) > 0:
        curNode = queue.pop()
        path.append(curNode)
        if curNode[0] == x2 and curNode[1] == y2:
            # 终点
            print_r(path)
            return True
        for dir in dirs:
            nextNode = dir(curNode[0], curNode[1])
            if maze[nextNode[0]][nextNode[1]] == 0:
                queue.append((nextNode[0], nextNode[1], len(path) - 1))  # 后续节点进队，记录哪个节点带他来的
                maze[nextNode[0]][nextNode[1]] = 2  # 标记为已经走过
    else:
        print("没有路")
        return False


maze_path_queue(1, 1, 8, 8)

 

链表

node 英 /nəʊd/ 美 /nod/  节点

linked list 链表

链表的创建和遍历

头插法-------------------------------尾插法

class Node:
　　def __init__(self,item):
　　　　self.item = item
　　　　self.next = Node

def create_linklist_head(li):
    head = Node(li[0])
    for element in li[1:]:
        node = Node(element)
        node.next = head

        head = node
        print(head.__dict__)
    return head

# 尾插入
def create_linklist_tail(li):
    head = Node(li[0])
    tail = head
    for element in li[1:]:
        node = Node(element)
        tail.next = node
        tail = node
    return head


def print_linklist(lk):
    while lk:
        print(lk.item,end=',')
        lk= lk.next

# 头插法
lk = create_linklist_head([1,2,3])
print(lk.__dict__)
print_linklist(lk)
# print(lk.next.item)

{'item': 2, 'next': <__main__.Node object at 0x0000000002258C50>}
{'item': 3, 'next': <__main__.Node object at 0x000000000225EAC8>}

{'item': 3, 'next': <__main__.Node object at 0x000000000225EAC8>}
3,2,1,

链表的插入和删除

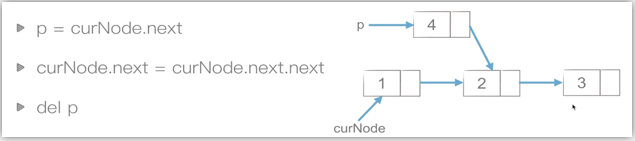
 单链表只能从前往后找

 

双链表

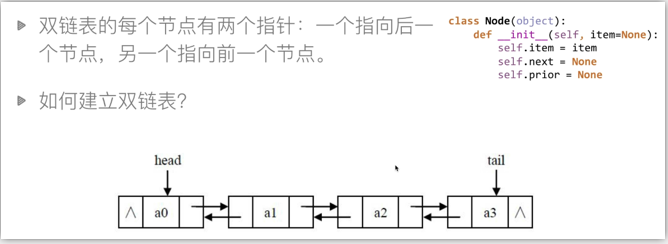
 总结