Hough圆检测和Hough直线检测思想类似，都是把直角坐标系中的一条直线或一个圆转换成另一个坐标系中的一个点。
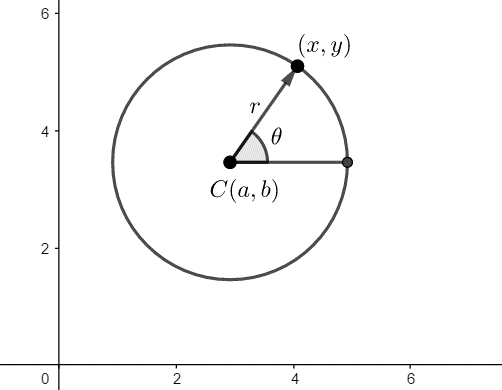
对于Hough圆，在直角坐标系中的一个圆 \(C\)，圆心为 \(C(a,b)\)，半径为 \(r\)，则圆上的每一点可以表示成
把 \(a\), \(b\) 写在左面，得
我们可以建立这样一个三维空间：对于原直角坐标系中的每一个圆，可以确定 \((a,b,r)\) 这样一个点，这个点即为新的三维空间中的点。
对于原直角坐标系，如果给定了 \((a,b)\)，则原坐标系以 \((a,b)\) 为圆心的所有不同半径的圆对应了新坐标空间中的一条直线。
在实际数字图像中，图像大小是有限的，图像本身是离散的，则对应的 \(r\) 取值也是有限的和离散的。
1. 直接检测Hough圆
下面说明怎样找出Hough圆。
我们假设图像已经二值化，背景为黑色，前景为白色。通常是进行Canny边缘检测形成二值图，否则如果是一个实心的白圆，将造成巨大干扰。Hough圆检测思路如下：
- 在图像上建立坐标系，比如以左上角为原点，向右为 \(x\) 正方向，向下为 \(y\) 正方向；
- 设计一个三维数组当做计数器 \(N(i,j,k)\)，\(i,j,k\) 分别对应 \(a,b,r\)，该计数器用来累计对应的前景像素，具体如下。
- 遍历每个像素，对每个像素，从最小指定半径开始，按给定步长依次增加半径，直到最大半径。如果在某一个半径上的圆通过某个前景像素，那么此时对应对 \((a,b,r)\) 的计数器 \(N(a,b,r)\) 的值加 \(1\)。
试想如果待检测图像中恰好有一个圆，那么最终在某个计数器位置 \(N(a_0,b_0,r_0)\) 位置的计数值会很大，而其他地方的计数值都为 \(0\)。而那个最佳计数器 \(a_0,b_0,r_0\) 就确定了一个圆。
在实际操作中，通常会设定一个阈值，超过该阈值的计数器的值都可以认为是有一个圆存在。
上述操作理论上完全没问题，但计算量比较大。例如，一张 \(500\times 500\) 这样小分辨率的图像，前景像素占 \(1/100\)，即有 \(2500\) 个像素白点。如果设半径步长为 \(1\)，即每次增加一个像素点的半径，半径从 \(0\) 到图像最大，考虑边缘，粗略估计半径变化大约 \(200\) 次，这样最终需要计算 \(2500 \times 200=5\times 10^5\) 次，也就是说这样的图片检测依次需要五十万次计算，为了提高效率，通常采用 Hough 梯度法。
2. Hough梯度法
- 对原图像进行边缘检测，获得二值图像。
- 对原图像分别进行一次 \(x\) 和 \(y\) 方向的 \(Sobel\) 算子，分别得到 \(x\) 和 \(y\) 方向的像素梯度值。有了两个方向的梯度值，就可以计算梯度的幅值和方向。如果是一个圆，梯度方向将指向圆心。
- 设置一个圆心二维计数器 \(N(i,j)\)，和上面的计数器相比，少了半径方向的维度，初始化为所有的 \(N(i,j)=0\)。
- 遍历Canny边缘二值图中所有的非零像素点，计算出其梯度方向，该梯度方向和非零像素点可以对应一条射线，起点为非零像素点，方向为梯度方向。把射线经过的位置 \((i,j)\) 的计数器 \(N(i,j) = N(i,j) + 1\)。
- 试想原图中有一个圆，那么这个圆上所有点都会让圆心处的计数器增\(1\)。所以根据设定的阈值，当计数器大于该阈值，就认为该计数器对应的点为一个圆心。
- 确定了圆心，再逐步增长半径寻找圆，这个过程和直接检测Hough圆类似。
综上可以看出，Hough梯度法是先想办法找出圆心，再去找半径。而不是像直接Hough圆检测一样去对每个前景点都进行圆心搜索。
我们据上面例子粗略计算一下。一张 \(500\times 500\) 这样小分辨率的图像，前景像素占 \(1/100\)，即有 \(2500\) 个像素白点。如果设半径步长为 \(1\)，半径从 \(0\) 到图像最大，考虑边缘，粗略估计半径变化大约 \(200\) 次。假设图上有 \(5\) 个圆。
这样，先找圆心，需要计算 \(2500\) 次，然后对 \(5\) 个圆，大约需要 \(5\times 200 = 1000\)次，总计 \(3500\) 次，相比效率为 \(5\times 10^5 / 3500 = 143\)，所以速度增快了两个数量级。
