Hough直线检测通过直角坐标系中（之后称直角坐标系）的点线关系和转换后的极坐标系（之后称为新坐标系）之间的对应关系，把直角坐标系中的直线检测转换成新坐标系中的点检测。
为了理解 Hough变换，先看一个简单的例子。

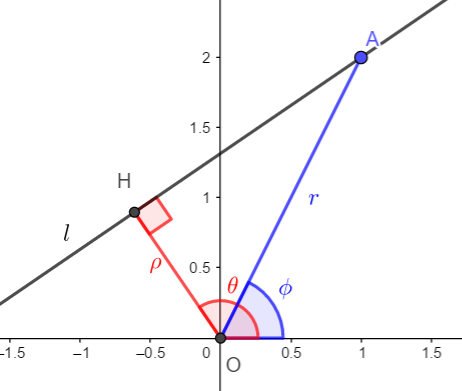
图1

其中 \(A\)为定点，直角坐标为 \(A(x,y)\)，极坐标表示为 \(A(r, \phi)\)。直线 \(l\) 可以绕 \(A\) 旋转。过原点作直线 \(l\) 的垂线，垂足 \(H\) 极坐标表示为 \((\rho, \theta)\)，当直线 \(l\) 绕 \(A\) 旋转的时候，\(H\) 的轨迹是一定的，也就是说，\(\rho, \theta\) 之间要满足一定的关系式，这个关系是什么呢？通过分析可以发现约束关系

\[\begin{aligned} \rho &= r cos(\phi-\theta) \\ &= r cos\phi cos\theta + r sin\phi sin\theta \end{aligned}\tag{1} \]

由根据 \(A\) 点极坐标与直角坐标的关系，知道

\[rcos\phi = x\\ rsin\phi = y \]

代入 \((1)\) 式，得

\[\rho = xcos\theta + ysin\theta \tag{2} \]

下面来解读以下这个式子。式 \((2)\) 表明，任意给一个定点 \((x,y)\)，过该点有无穷多条直线，随着直线的变化，根据原点到这些直线的距离 \(\rho\) 和其与 \(x\) 轴的夹角 \(\theta\) ，可以得到一条曲线。
下面我们考虑一条定直线 \(m: y=x+1\)，上面取的 \(A=(1,2)\) 在直线 \(m\) 上，另外取 \(B=(0,1)\in m, C=(-1,0)\in m\)， 同上，也可以分别确定一个方程。
由 \(A,B,C\)三点决定了三个方程如下：

\[\rho = cos\theta + 2sin\theta \tag{3} \]

\[\rho = sin\theta \tag{4} \]

\[\rho = -cos\theta \tag{5} \]

我们可以以 \(\theta\) 为横坐标，以 \(\rho\) 为纵坐标画出曲线，事实上这是个三角函数，其曲线如下（\(\rho\) 取绝对值）
图2 \(\theta, \rho\) 关系图

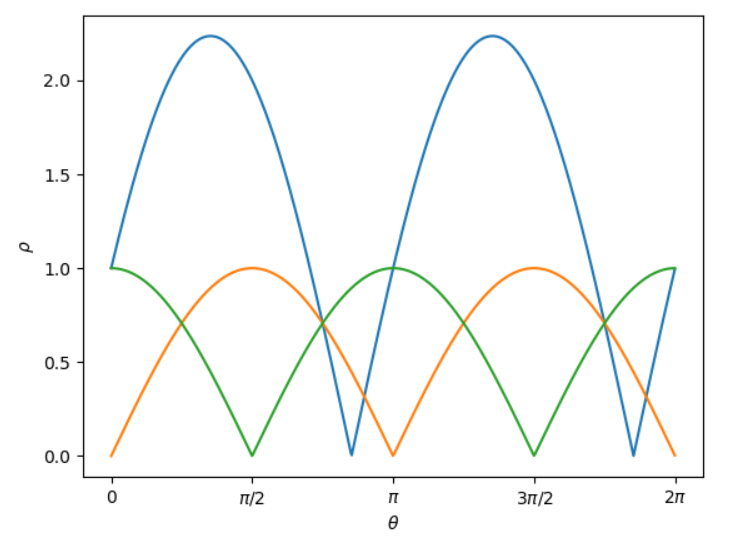
图2

过 \(A, B, C\) 三点决定的方程在新坐标系中各决定了一条曲线，而曲线的交点，就是方程 \((3),(4),(5)\) 的解。事实上，只要是在直线 \(p\) 上的点决定新坐标的方程，都会过该交点。联系直角坐标系和方程 \(y=x+1\)，可以算出，这个交点是 \(\rho= 1/\sqrt{2}, \theta = 135^{\circ}=3\pi/4\)。

事实上，在直角坐标系中，如果多个点都在某个直线 \(q\) 上，那么它们在新坐标系中都有一个共同的交点。那怎样实现 Hough 变换呢？

我们可以把图2网格化，即把 \(\theta\) 分成 \(m\) 份， \(\rho\) 分成 \(n\) 份，设一个计数器 \(C(i,j),i\in[1,...,m], j\in[1,...,n]\)。假设现在二维数学图像（离散）上有若干点，每个点就可以决定一条曲线，这个曲线依次经过的一系列格子上，对应的计数器 \(C(i,j)\) 加 \(1\)，这样，扫描完所有点之后，就可以得到一个计数器表。就像图2中的交点一样，如果直角坐标系中真有一条直线，那它上面的点都会映射到新坐标中的一点，对应的格子的计数值就大。如果某个格子上的计数超过阈值，说明有一条直线存在，把此时的这个格子对应的 \((\rho, \theta)\) 值代入方程 \((2)\)，就可以得到对应的直角坐标系中的直线。