定义

设 \(A=(a_{ij})_{n\times n}\)，称 \(A\) 的特征值的集合为 \(A\) 的谱，称 \(A\) 的特征值的模的最大值为 \(A\) 的谱半径，记为 \(\rho(A)\). 记

\[R_i = |a_{i1}|+\cdots + |a_{ii-1}|+|a_{ii+1}|+\cdots + |a_{in}|, \]

\[C_i = \{z| |z-a_{ii}|\le R_i\} \]

称之为 \(A\) 的第i个盖尔圆；
称 \(G = \cup_{i=1}^n C_i\) 为 \(A\) 的盖尔圆系。

对于盖尔圆，说人话就是，以某一行的处于对角线元素为圆心，以该行其余元素的模的和为半径的一个圆，这里考虑的是复矩阵，所以是模，而不是绝对值。

定理

矩阵 \(A\) 的特征值必定在 \(A\) 的盖尔圆系中。

谱半径的估计

设 \(A=(a_{ij})_{n\times n}\)，

\[\rho_1 = \max\limits_{1\le i\le n}\{\sum\limits_{j=1}^n |a_{ij}| \},\\ \rho_2 = \max\limits_{1\le j\le n}\{\sum\limits_{i=1}^n |a_{ij}| \}\\ \]

则 \(rho(A)\le min(\rho_1, rho_2)\)。
说人话就是，谱半径小于等于<最大列模和>和<最大行模和>的最小值。

题目

设矩阵 \(A=\left( \begin{matrix} 1 & 2 & 3 & 4\\ 2 & 3 & 4 & 1\\ 3 & 4 & 1 & 2\\ 1 & 1 & 2 & 3 \end{matrix} \right)\)，试证：\(\rho(A)\lt 10\)。

解答

根据<行模和>小于等于10，由谱半径的估计，容易证明\(\rho(A)\le 10\)。
如果再证明10不是特征值，其实不够，因为盖尔圆是再复平面的一个圆，除了(10,0i)外还有无数模为10的点。
可以用图像画出所有盖尔圆，即圆心是对角线元素（复数，本题中虚部为0），可以看出，盖尔圆的并集中模最大的点为(10,0)，其余点的模均小于10，此时再证明10不是特征值，即可说明 \(\rho(A)\lt 10\)。
盖尔圆如下图所示，两条黑线交点为原点：

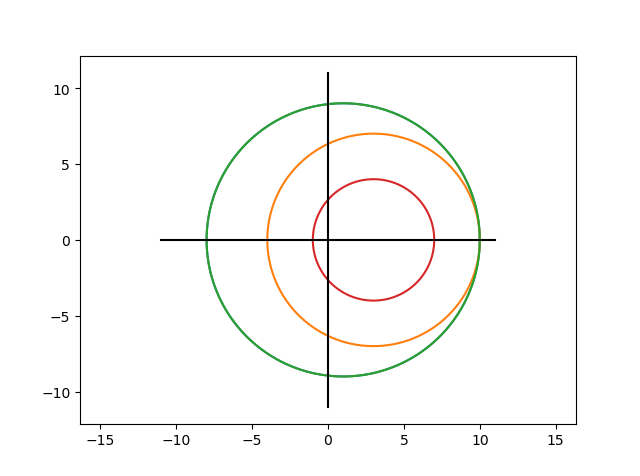
要说明10不是特征值，证明 \(|A-10I|\ne 0\) 即可，此处略。