题目描述

编程实现线性判别分析，并给出西瓜数据集3.0\(\alpha\)上的结果。

解答

直接根据公式计算即可，根据公式（3.39）

\[w = S_w^{-1}(\mu_0 - \mu_1) \]

其中\(\mu_0\), \(\mu_1\) 分别是0类（坏瓜）和1类（好瓜）的各个属性的均值向量，其长度就是属性数。\(S_w\) 是类内散度矩阵，定义为是（3.33），

\[\begin{aligned} S_w &= \sum_0 + \sum_1 \\ &= \sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T + \sum_{x\in X_1} (x-\mu_1)(x-\mu_1)^T \\ \end{aligned} \]

效果如下，蓝色的线就是投影的线：

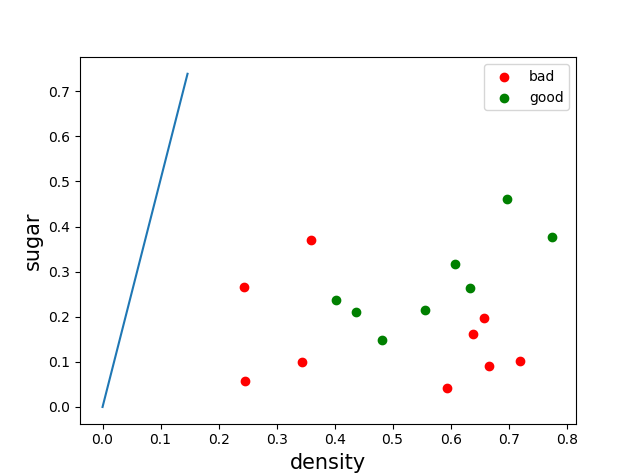
编程实现很简单，用python的broadcasting，可以简化代码。

import numpy as np
import matplotlib.pyplot as plt

# 西瓜数据集
# 编号,密度,含糖率,好1（坏0）瓜
data = """
1,0.697,0.46,1
2,0.774,0.376,1
3,0.634,0.264,1
4,0.608,0.318,1
5,0.556,0.215,1
6,0.403,0.237,1
7,0.481,0.149,1
8,0.437,0.211,1
9,0.666,0.091,0
10,0.243,0.267,0
11,0.245,0.057,0
12,0.343,0.099,0
13,0.639,0.161,0
14,0.657,0.198,0
15,0.36,0.37,0
16,0.593,0.042,0
17,0.719,0.103,0
"""

def get_data(data): # 这里就不划分训练和测试集
    X = [(item.split(',')) for item in data.split()]
    X = np.array(X, dtype=np.float)
    y = X[:, 3]
    X = X[:,[1,2]]
    return X, y

X, y = get_data(data)
X0, y0 = X[y==0], y[y==0]
X1, y1 = X[y==1], y[y==1]

mu0, mu1 = np.mean(X0, axis=0), np.mean(X1, axis=0)
Sw = (X0 - mu0).T.dot(X0 - mu0) + (X1 - mu1).T.dot(X1 - mu1)
w = np.linalg.inv(Sw).dot(mu0 - mu1)
print(w)

# 可视化
plt.scatter(X0[:,0], X0[:,1], c='r', label="bad")
plt.scatter(X1[:,0], X1[:,1], c='g', label="good")
plt.plot([0, -1*w[0]], [0, -1*w[1]]) # 方便显示，w同时乘-1，都是同一条直线
plt.legend()
plt.xlabel("density", fontsize=15)
plt.ylabel("sugar", fontsize=15)
plt.show()