题目描述：
编程实现对率回归，并给出西瓜数据集3.0\(\alpha\)上的结果。
编程实现
对数几率回归最小化损失函数（西瓜书公式3.27）如下：
\[l(\beta) = \sum_{i=1}^m (-y_i\beta ^T x_i + ln(1+e^{\beta^T x_i}))
\]
证明：
\[suppose: g_i = g_i(\beta) = e^{\beta^T x_i} \\
g_i > 0 \\
g_i' = g_i x_i \\
\nabla l(\beta) = \sum_{i=1}^m (-y_i x_i + \frac{g_i'}{1+g_i}) = \sum_{i=1}^m (-y_i x_i + \frac{g_i}{1+g_i}x_i) \\
\]
更新方式为
\[w \gets w - \alpha \nabla f(w)
\]
\(\alpha\) 为步长。
先展示结果
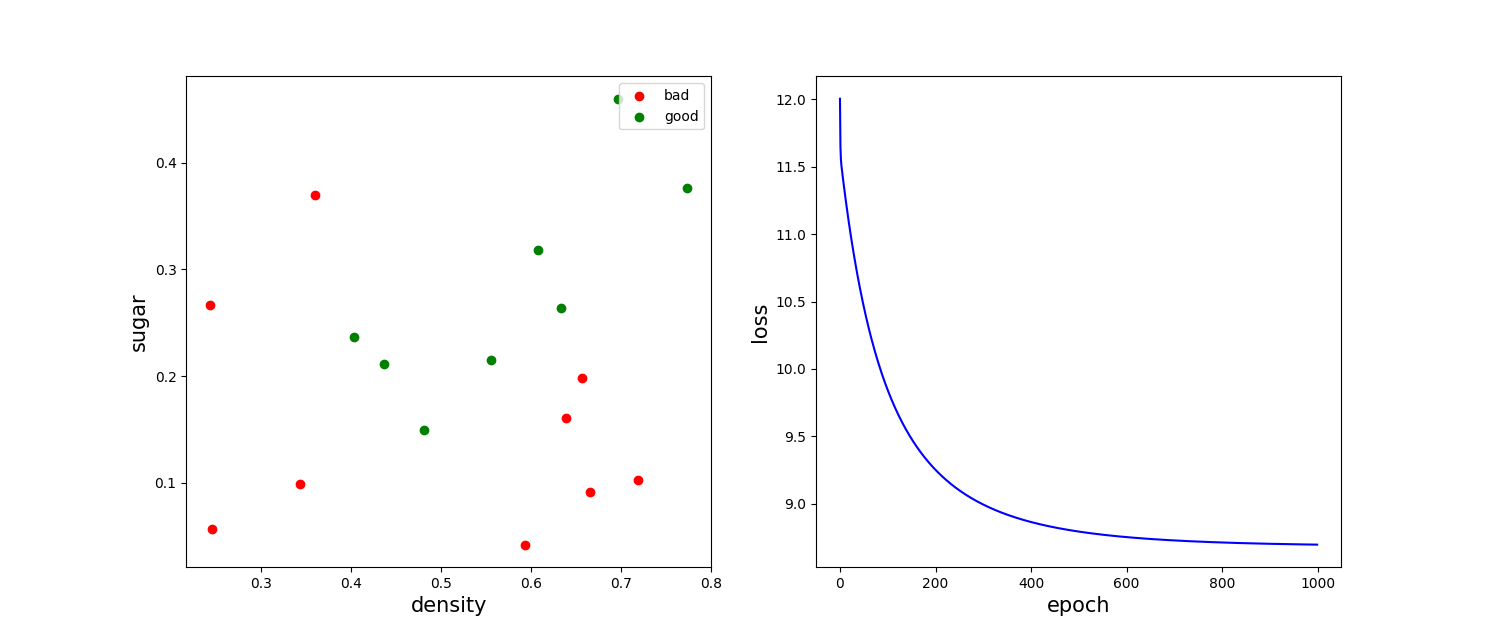
Accuracy = 0.71
import numpy as np
import matplotlib.pyplot as plt
def loss(X, y, beta): # 根据损失公式计算当前参数 beta 时打损失
loss1 = np.sum(-y * (X.dot(beta)))
loss2 = np.sum(np.log(1 + np.exp(X.dot(beta))))
return loss1 + loss2
def grad(X, y, beta): # 根据梯度公式计算当前参数 beta 时的一阶梯度
g = np.exp(X.dot(beta))
grad1 = -y.dot(X)
grad2 = (g / (1.0 + g)).dot(X)
return grad1 + grad2
def get_data(data): # 根据原始数据得到增加1截距项X,y，这里就不化分训练和测试集
X = [(item.split(',')) for item in data.split()]
X = np.array(X, dtype=np.float)
y = X[:, 3]
X = X[:,[1,2]]
X = np.hstack([np.ones((len(X),1)), X])
return X, y
def get_acc(X, y_true, beta): # 计算准确率
y_pred = 1. / (1 + np.exp(-X.dot(beta)))
y_pred = np.array(y_pred >= 0.5, dtype=np.float)
acc = (y_pred == y_true).sum() / len(y_pred)
return acc
def logistic_regression(X, y):
episilon = 1e-5 # 如果两次更新损失小于次，停止更新
max_epoch = 1000 # 最大迭代次数
alpha = 0.1 # 学习率
beta = np.random.random(X.shape[1]) # 待学习参数
losses = [] # 记录损失
for i in range(max_epoch):
last_beta = beta.copy()
grad_beta = grad(X, y, beta) # 计算梯度
beta -= alpha * grad_beta # 梯度下降法
if (abs(loss(X,y,beta) - loss(X,y,grad_beta))<episilon):
break
losses.append(loss(X, y, beta)) # 记录损失
acc = get_acc(X, y, beta)
return acc, losses
# 编号,密度,含糖率,好1（坏0）瓜
data = """
1,0.697,0.46,1
2,0.774,0.376,1
3,0.634,0.264,1
4,0.608,0.318,1
5,0.556,0.215,1
6,0.403,0.237,1
7,0.481,0.149,1
8,0.437,0.211,1
9,0.666,0.091,0
10,0.243,0.267,0
11,0.245,0.057,0
12,0.343,0.099,0
13,0.639,0.161,0
14,0.657,0.198,0
15,0.36,0.37,0
16,0.593,0.042,0
17,0.719,0.103,0
"""
X, y = get_data(data)
acc, losses = logistic_regression(X, y) # 获取准确率和损失list
print(f"Accuracy = {acc:.2}")
# 可视化
# ax1 显示原数据
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(12,4))
ax1.scatter(X[y==0,1], X[y==0,2], c='r', label="bad")
ax1.scatter(X[y==1,1], X[y==1,2], c='g', label="good")
ax1.set_xlabel("density", fontsize=15)
ax1.set_ylabel("sugar", fontsize=15)
ax1.legend()
# ax2 显示损失变化
ax2.plot(range(len(losses)), losses, 'b')
ax2.set_xlabel("epoch", fontsize=15)
ax2.set_ylabel("loss", fontsize=15)
plt.show()
