生成模型——自回归模型详解与PixelCNN构建
生成模型——自回归模型详解与PixelCNN构建
自回归模型(Autoregressive models)
深度神经网络生成算法主要分为三类:
- 生成对抗网络(Generative Adversarial Network, GAN)
- 可变自动编码器(Variational Autoencoder, VAE)
- 自回归模型(Autoregressive models)
VAE已经在《变分自编码器(VAE)原理与实现(tensorflow2.x)》中进行了介绍。GAN的详细信息参考《深度卷积生成对抗网络(DCGAN)原理与实现(采用Tensorflow2.x)》。将在这里介绍鲜为人知的自回归模型,尽管自回归在图像生成中并不常见,但自回归仍然是研究的活跃领域,DeepMind的WaveNet使用自回归来生成逼真的音频。在本文中,将介绍自回归模型并构建PixelCNN模型。
简介
Autoregressive中的“Auto”意味着自我(self),而机器学习术语的回归(regress)意味着预测新的值。将它们放在一起,自回归意味着我们使用模型基于模型的过去数据点来预测新数据点。
设图像的概率分布是
p
(
x
)
p(x)
p(x)是像素的联合概率分布
p
(
x
1
,
x
2
,
…
x
n
)
p(x_1, x_2, …x_n)
p(x1,x2,…xn),由于高维数很难建模。在这里,我们假设一个像素的值仅取决于它之前的像素的值。换句话说,当前像素仅以其前一像素为条件,即
p
(
x
i
)
=
p
(
x
i
∣
x
i
−
1
)
p
(
x
i
−
1
)
p(x_i) = p(x_i | x_{i-1}) p(x_{i-1})
p(xi)=p(xi∣xi−1)p(xi−1),我们就可以将联合概率近似为条件概率的乘积:
p
(
x
)
=
p
(
x
n
,
x
n
−
1
,
…
,
x
2
,
x
1
)
p(x) = p(x_n, x_{n-1}, …, x_2, x_1)
p(x)=p(xn,xn−1,…,x2,x1)
p
(
x
)
=
p
(
x
n
∣
x
n
−
1
)
.
.
.
p
(
x
3
∣
x
2
)
p
(
x
2
∣
x
1
)
p
(
x
1
)
p(x) = p(x_n | x_{n-1})... p(x_3 | x_2) p(x_2 | x_1) p(x_1)
p(x)=p(xn∣xn−1)...p(x3∣x2)p(x2∣x1)p(x1)
举一个具体的例子,假设在图像的中心附近包含一个红色的苹果,并且该苹果被绿叶包围,在此情况下,假设仅存在两种可能的颜色:红色和绿色。
x
1
x_1
x1是左上像素,所以
p
(
x
1
)
p(x_1)
p(x1)表示左上像素是绿色还是红色的概率。如果
x
1
x_1
x1为绿色,则其右边
p
(
x
2
)
p(x_2)
p(x2)的像素也可能也为绿色,因为它可能会有更多的叶子。但是,尽管可能性较小,但它也可能是红色的。
继续进行计算,我们最终将得到红色像素。从那个像素开始,接下来的几个像素也很可能也是红色的,这比必须同时考虑所有像素要简单得多。
PixelRNN
PixelRNN由DeepMind于2016年提出。正如名称RNN(Recurrent Neural Network, 递归神经网络)所暗示的那样,该模型使用一种称为长短期记忆(LSTM)的RNN来学习图像的分布。它在LSTM中的一个步骤中一次读取图像的一行,并使用一维卷积层对其进行处理,然后将激活信息馈送到后续层中以预测该行的像素。
由于LSTM运行缓慢,因此需要花费很长时间来训练和生成样本。因此,我们不会对其进行过多的研究,而将注意力转移到同一论文中提出的一种变体——PixelCNN。
使用TensorFlow 2构建PixelCNN模型
PixelCNN仅由卷积层组成,使其比PixelRNN快得多。在这里,我们将为使用MNIST数据集训练一个简单的PixelCNN模型。
输入和标签
MNIST由28 x 28 x 1灰度数字手写数字组成。它只有一个通道:

在本实验中,通过将图像转换为二进制数据来简化问题:0代表黑色,1代表白色:
def binarize(image, label):
image = tf.cast(image, tf.float32)
image = tf.math.round(image/255.)
return image, tf.cast(image, tf.int32)
该函数需要两个输入——图像和标签。该函数的前两行将图像转换为二进制float32格式,即0.0或1.0。并且,我们将二进制图像转换为整数并返回,以遵循使用整数作为标签的惯例而已。返回的数据,将作为网络训练的输入和标签,都是28 x 28 x 1的二进制MNIST图像,它们仅在数据类型上有所不同。
掩膜
与PixelRNN逐行读取不同,PixelCNN在图像中从左到右,从上到下滑动卷积核。当执行卷积以预测当前像素时,传统的卷积核能够看到当前输入像素及其周围的像素,其中包括当前像素之后的像素信息,这与在简介部分的条件概率假设相悖。
为了避免这种情况,我们需要确保CNN在预测输出像素
x
i
x_i
xi时不会看到输入像素
x
i
x_i
xi。
这是通过使用掩膜卷积来实现的,其中在执行卷积之前将掩膜应用于卷积核权重。下图显示了一个7 x 7卷积核的掩膜,其中从中心开始的权重为0。这会阻止CNN看到它正在预测的像素(卷积核的中心)以及所有之后的像素。这称为A型掩膜,仅应用于输入层。
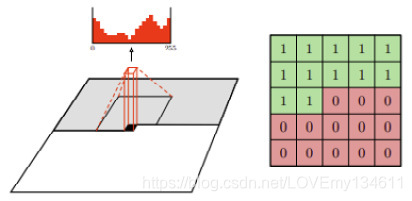
由于中心像素在第一层中被遮挡,因此我们不再需要在后面的层中隐藏中心要素。实际上,我们需要将卷积核中心设置为1,以使其能够读取先前层的特征,这称为B型掩膜。
实现自定义层
现在,我们将为掩膜卷积创建一个自定义层。我们可以使用从基类tf.keras.layers.Layer继承的子类在TensorFlow2.x中创建自定义层,以便将能够像使用其他Keras层一样使用它。以下是自定义层类的基本结构:
class MaskedConv2D(tf.keras.layers.Layer):
def __init__(self):
...
def build(self, input_shape):
...
def call(self, inputs):
...
return output
build()将输入张量的形状作为参数,我们将使用此信息来确保创建正确形状的变量。构建图层时,此函数仅运行一次。我们可以通过声明不可训练的变量或常量来创建掩码,以使TensorFlow知道它不需要梯度来反向传播:
def build(self, input_shape):
self.w = self.add_weight(shape=[self.kernel,
self.kernel,
input_shape[-1],
self.filters],
initializer='glorot_normal',
trainable=True)
self.b = self.add_weight(shape=(self.filters,),
initializer='zeros',
trainable=True)
mask = np.ones(self.kernel**2, dtype=np.float32)
center = len(mask)//2
mask[center+1:] = 0
if self.mask_type == 'A':
mask[center] = 0
mask = mask.reshape((self.kernel, self.kernel, 1, 1))
self.mask = tf.constant(mask, dtype='float32')
call()用来执行前向传递。在掩膜卷积层中,在使用低级tf.nn API执行卷积之前,我们将权重乘以掩码后将下半部分的值设为零:
def call(self, inputs):
masked_w = tf.math.multiply(self.w, self.mask)
output=tf.nn.conv2d(inputs, masked_w, 1, "SAME") + self.b
return output
网络架构
PixelCNN架构非常简单。在使用A型掩膜的第一个7 x 7 conv2d图层之后,有几层带有B型掩膜的残差块:
Model: "PixelCnn"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 28, 28, 1)] 0
_________________________________________________________________
masked_conv2d_22 (MaskedConv (None, 28, 28, 128) 6400
_________________________________________________________________
residual_block_7 (ResidualBl (None, 28, 28, 128) 53504
_________________________________________________________________
residual_block_8 (ResidualBl (None, 28, 28, 128) 53504
_________________________________________________________________
residual_block_9 (ResidualBl (None, 28, 28, 128) 53504
_________________________________________________________________
residual_block_10 (ResidualB (None, 28, 28, 128) 53504
_________________________________________________________________
residual_block_11 (ResidualB (None, 28, 28, 128) 53504
_________________________________________________________________
residual_block_12 (ResidualB (None, 28, 28, 128) 53504
_________________________________________________________________
residual_block_13 (ResidualB (None, 28, 28, 128) 53504
_________________________________________________________________
conv2d_2 (Conv2D) (None, 28, 28, 64) 8256
_________________________________________________________________
conv2d_3 (Conv2D) (None, 28, 28, 1) 65
=================================================================
Total params: 389,249
Trainable params: 389,249
Non-trainable params: 0
下图说明了PixelCNN中使用的残差块架构:

交叉熵损失
交叉熵损失也称为对数损失,它衡量模型的性能,其中输出的概率在0到1之间。以下是二进制交叉熵损失的方程,其中只有两个类,标签y可以是0或1,
p
(
x
)
p(x)
p(x)是模型的预测:
B
C
E
=
−
1
N
∑
i
=
1
N
(
y
i
l
o
g
p
(
x
)
+
(
1
−
y
i
)
l
o
g
(
1
−
p
(
x
)
)
)
BCE = -\frac1N\sum_{i=1}^N(y_ilogp(x)+(1-y_i)log(1-p(x)))
BCE=−N1i=1∑N(yilogp(x)+(1−yi)log(1−p(x)))
在PixelCNN中,单个图像像素用作标签。在二值化MNIST中,我们要预测输出像素是0还是1,这使其成为使用交叉熵作为损失函数的分类问题。
最后,编译和训练神经网络,我们对损失和度量均使用二进制交叉熵,并使用RMSprop作为优化器。有许多不同的优化器可供使用,它们的主要区别在于它们根据过去的统计信息调整学习率的方式。没有一种最佳的优化器可以在所有情况下使用,因此建议尝试使用不同的优化器。
编译和训练pixelcnn模型:
pixelcnn = SimplePixelCnn()
pixelcnn.compile(
loss = tf.keras.losses.BinaryCrossentropy(),
optimizer=tf.keras.optimizers.RMSprop(learning_rate=0.001),
metrics=[ tf.keras.metrics.BinaryCrossentropy()])
pixelcnn.fit(ds_train, epochs = 10, validation_data=ds_test)
接下来,我们将根据先前的模型生成一个新图像。
采样生成图片
训练后,我们可以通过以下步骤使用该模型生成新图像:
- 创建一个具有与输入图像相同形状的空张量,并用
1填充。将其馈入网络并获得 p ( x 1 ) p(x1) p(x1),即第一个像素的概率。 - 从 p ( x 1 ) p(x_1) p(x1)进行采样,并将采样值分配给输入张量中的像素 x 1 x_1 x1。
- 再次将输入提供给网络,并对下一个像素执行步骤2。
- 重复步骤2和3,直到生成 x N x_N xN。
自回归模型的一个主要缺点是它生成速度慢,因为需要逐像素生成,而无法并行化。以下图像是我们的PixelCNN模型经过100个训练周期后生成的。它们看起来还不太像正确的数字,但我们现在可以凭空生成新图像。可以通过训练更长的模型并进行一些超参数调整来生成更好的数字。

完整代码
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras.activations import relu
from tensorflow.keras.models import Sequential
import tensorflow_datasets as tfds
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
print(tf.__version__)
(ds_train, ds_test), ds_info = tfds.load(
'mnist',
split=['test', 'test'],
shuffle_files=True,
as_supervised=True,
with_info=True)
fig = tfds.show_examples(ds_train, ds_info)
def binarize(image, label):
image = tf.cast(image, tf.float32)
image = tf.math.round(image/255.)
return image, tf.cast(image, tf.int32)
ds_train = ds_train.map(binarize)
ds_train = ds_train.cache() # put dataset into memory
ds_train = ds_train.shuffle(ds_info.splits['train'].num_examples)
ds_train = ds_train.batch(128)
ds_test = ds_test.map(binarize).batch(128).prefetch(64)
class MaskedConv2D(layers.Layer):
def __init__(self, mask_type, kernel=5, filters=1):
super(MaskedConv2D, self).__init__()
self.kernel = kernel
self.filters = filters
self.mask_type = mask_type
def build(self, input_shape):
self.w = self.add_weight(shape=[
self.kernel,
self.kernel,
input_shape[-1],
self.filters],
initializer='glorot_normal',
trainable=True)
self.b = self.add_weight(shape=(self.filters,),
initializer='zeros',
trainable=True)
# Create Mask
mask = np.ones(self.kernel ** 2, dtype=np.float32)
center = len(mask) // 2
mask[center+1:] = 0
if self.mask_type == 'A':
mask[center] = 0
mask = mask.reshape((self.kernel, self.kernel, 1, 1))
self.mask = tf.constant(mask, dtype='float32')
def call(self, inputs):
# mask the convolution
masked_w = tf.math.multiply(self.w, self.mask)
# preform conv2d using low level API
output = tf.nn.conv2d(inputs, masked_w, 1, 'SAME') + self.b
return tf.nn.relu(output)
class ResidualBlock(layers.Layer):
def __init__(self, h=32):
super(ResidualBlock, self).__init__()
self.forward = Sequential([
MaskedConv2D('B', kernel=1, filters=h),
MaskedConv2D('B', kernel=3, filters=h),
MaskedConv2D('B', kernel=1, filters=2*h),
])
def call(self, inputs):
x = self.forward(inputs)
return x + inputs
def SimplePixelCnn(
hidden_features=64,
output_features=64,
resblocks_num=7):
inputs = layers.Input(shape=[28, 28, 1])
x = inputs
x = MaskedConv2D('A', kernel=7, filters=2*hidden_features)(x)
for _ in range(resblocks_num):
x = ResidualBlock(hidden_features)(x)
x = layers.Conv2D(output_features, (1,1), padding='same', activation='relu')(x)
x = layers.Conv2D(1, (1,1), padding='same', activation='sigmoid')(x)
return tf.keras.Model(inputs=inputs, outputs=x, name='PixelCnn')
pixel_cnn = SimplePixelCnn()
pixel_cnn.summary()
pixel_cnn.compile(
loss=tf.keras.losses.BinaryCrossentropy(),
optimizer=tf.keras.optimizers.RMSprop(learning_rate=0.001),
metrics=[tf.keras.losses.BinaryCrossentropy()]
)
grid_row = 5
grid_col = 5
batch = grid_row * grid_col
h = w = 28
images = np.ones((batch,h,w,1), dtype=np.float32)
for row in range(h):
for col in range(w):
prob = pixel_cnn.predict(images)[:, row,col,0]
pixel_samples = tf.random.categorical(
tf.math.log(np.stack([1-prob,prob],1)),1
)
#print(pixel_samples.shape)
images[:,row,col,0] = tf.reshape(pixel_samples, [batch])
# Display
f, axarr = plt.subplots(grid_row, grid_col, figsize=(grid_col*1.1,grid_row))
i = 0
for row in range(grid_row):
for col in range(grid_col):
axarr[row,col].imshow(images[i,:,:,0], cmap='gray')
axarr[row,col].axis('off')
i += 1
f.tight_layout(0.1, h_pad=0.2, w_pad=0.1)
plt.show()



