二叉树、B树、B+树、红黑树

树的概念

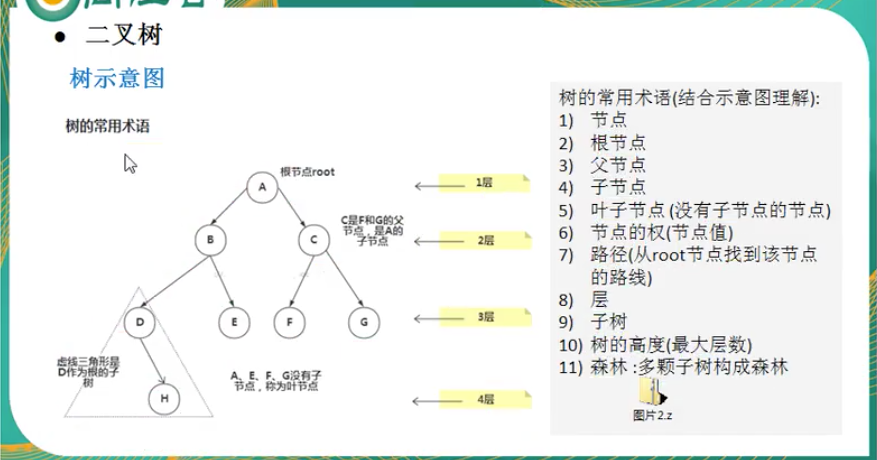
二叉树的概念

每个节点最多有2个子节点。

满二叉树

所有的叶子节点都在最后一层。

节点的总数为 2^n -1 ,n为层数。

完全二叉树

所有叶子节点在最后一层或倒数第二层。

也就是说，满二叉树，是一种特殊的完全二叉树。

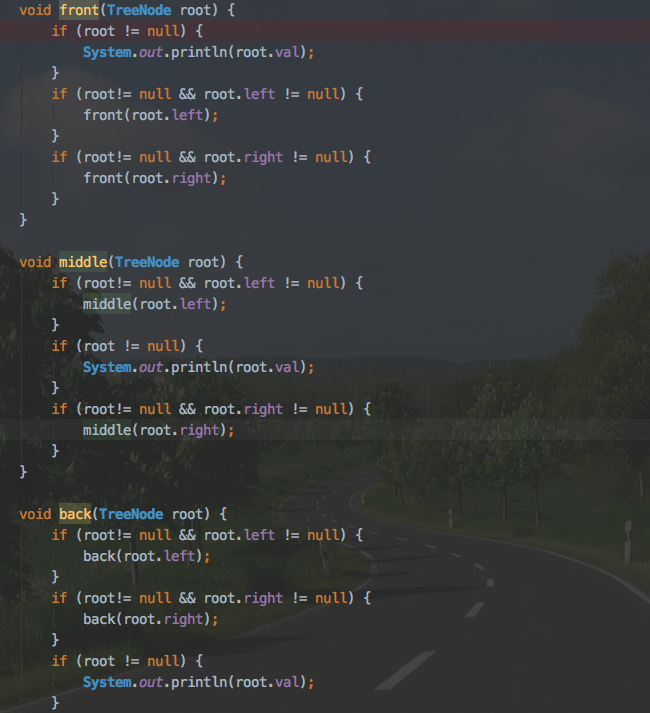
前序中序后序遍历(以递归的方式)

这里的前中后指的是父节点的位置。

前序：root，左，右
中序：左，root，右
后序：左，右，root

二叉搜索树（BST）

左子树的所有节点都比root小，右子树则大。

这就相当于之前在车上玩的游戏，猜一个数，大了还是小了，直到猜中那个数。思想是类似的。

平衡二叉树（AVL树）

别名：AVL树，是两个科学家的名字缩写。

平衡指的是，左右两边的节点层级的差不大于1。是在二叉搜索树的基础上加了一个平衡的概念。

左子树的所有节点都比root小，右子树则大。

它是一种基于二分法策略提高数据查找速度的二叉树结构。

B树

B-Tree，不读作B减树

B树与二叉查找树的不同之处在于，B树是多路的，也叫做平衡多路查找树。

B树的阶：B树中所有节点的孩子节点数的最大值，也就是每个节点最多包含的孩子。K取决于磁盘页的大小。

MySQL的索引为什么要用B-Tree，因为树的查询效率高。因为树的结构是非线性的，在插入的时候，已经将数据以指定形式存储。

为什么不用BST，BST的时间复杂度是O(logN)。

磁盘IO次数等于索引树的高度，最坏情况下，磁盘IO次数等于树的最高高度。为了减少磁盘IO次数，将原本瘦高的BST，改为矮胖的B-Tree。这也是B-Tree诞生的背景。

B+树

B+树是基于B树的一个变体，有更高的查询性能。

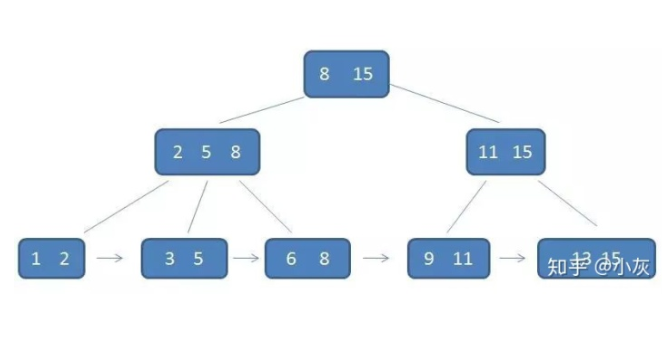
每个父节点的元素都出现在子节点中。

B+树的中间节点没有卫星数据，同样大小的磁盘页可以存储更多的节点元素。

B+树的结构比B-树更矮胖，查询时IO次数更少。查询性能更稳定，范围查询简便。

为什么说B+树更稳定，因为每次查找都必须查找到叶子节点，而B树最坏的情况下查到叶子节点。

红黑树

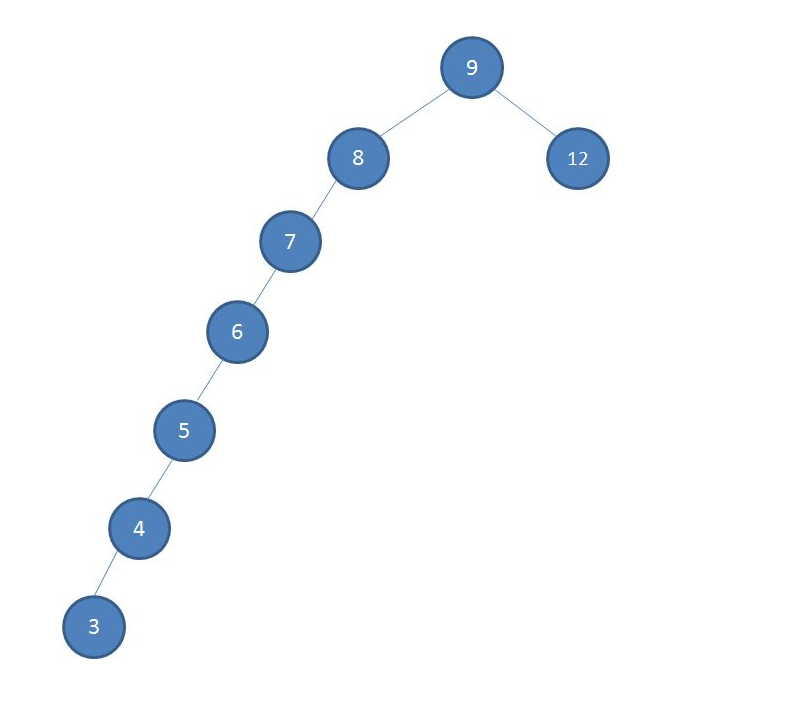
为什么要有红黑树这种数据结构？

BST的一个缺陷时，当频繁插入某些数据时，会导致二叉树的高度快速增加。

红黑树的定义：

• 节点是红色或黑色
• 根节点是黑色
• 红色节点的两个子节点一定是黑色
• 从任意节点到自己的叶子节点，经过的黑色节点数都是相同的
• 每个叶子节点都是黑色的空节点（NIL）

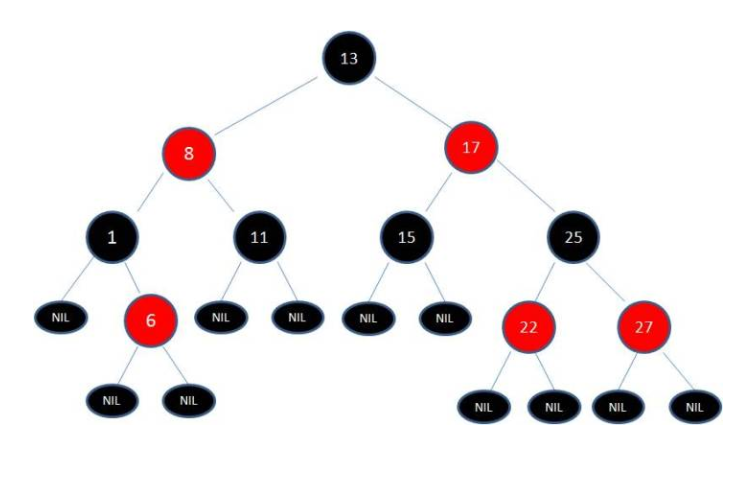
这种规则就限制了，红黑树从根到叶子的最长路径，不会超过最短路径的2倍。

调整的方式：

• 变色
• 旋转（左旋转、右旋转）