深入浅出统计学第七章 几何分布,二项分布,柏松分布
简介
<深入浅出统计学>第七章详细介绍了三种概率分布及其应用,而我们则将进行程序编写,来计算这三种概率分布.
几何分布
scipy几何分布原文地址
下面是书中一些重要公式的代码实现,此处我们直接调用scipy的类库,不再自己编写。首先当然是滑雪问题,固执的查德先生明明只有百分之二十的机会,一次滑雪成功,可他却分要不成功便成仁.为了我们的这位倒霉朋友的生命安全着想,看来我们是时候启动我们的计算机了.
from scipy.stats import geom
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
p = 0.2# P(X > r) = q ** r
print(geom.sf(2,p)) # pmf(r,p),当成功概率为p时,第一次成功需要r次以上的概率
# P(X <= r) = 1 - q ** r
print(geom.cdf(2,p)) # cdf(r,p),当成功概率为p时,r次及以内成功的概率
# P(X = 4) = p * q ** (r-1)
print(geom.pmf(4,p)) # pmf(r,p),当成功概率为p时,第r次成功的概率
# 额外的
print(geom.ppf(0.99, p)) # ppf(q,p),当成功概率为p时,想要获取q的概率,需要尝试的次数0.64
0.36
0.10240000000000003
21.0
print(geom.var(p)) # 方差 Var(X) = q/(p ** 2)
print(geom.mean(p)) # 均值,也就是期望E(X) = 1/p
print(geom.std(p)) # 标准差20.0
5.0
4.47213595499958
例题
为了更好的让查德先生了解自己的作死行为,我们还是不得比使用一些更直观的方法——表格与图标。(绘制P280的表格与图表如下,P282的表格与图标只需简单修改以下代码,此处不再冗余操作:)
x = np.arange(1,9)
import pandas as pd
df_Gemo_Table = pd.DataFrame({
"P(X=x)":geom.pmf(x,p),
"xP(X=x)":x * geom.pmf(x,p),
"xP(X<=x)":(x * geom.pmf(x,p)).cumsum()})
df_Gemo_Table| P(X=x) | xP(X<=x) | xP(X=x) | |
|---|---|---|---|
| 0 | 0.200000 | 0.200000 | 0.200000 |
| 1 | 0.160000 | 0.520000 | 0.320000 |
| 2 | 0.128000 | 0.904000 | 0.384000 |
| 3 | 0.102400 | 1.313600 | 0.409600 |
| 4 | 0.081920 | 1.723200 | 0.409600 |
| 5 | 0.065536 | 2.116416 | 0.393216 |
| 6 | 0.052429 | 2.483418 | 0.367002 |
| 7 | 0.041943 | 2.818962 | 0.335544 |
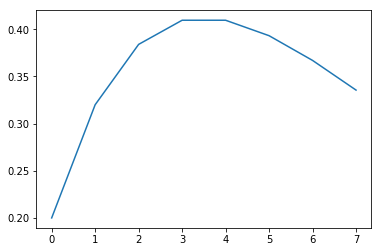
df_Gemo_Table ['xP(X = x)']。plot()
plt.show()二次分布
而除了我们的倒霉查德先生以外,还有一位不学习只能蒙题的老学渣,为了让他浪子回头,我们又不得不动用我们的双手和键盘连做点事情了。(二次分布的语法与几何分布是类似的,如下:),不过要算五十道题的二次分布似乎很麻烦(笔算),我们先算算四道问题的。
from scipy.stats import binom
print("假设四道四个选项的单项选择题,随便蒙,那么此时")
print("四道问题中答对零道的概率为",binom.pmf(0,4,0.25))
print("四道问题中答对一道的概率为",binom.pmf(1,4,0.25))
print("四道问题中答对两道的概率为",binom.pmf(2,4,0.25))
print("四道问题中答对三道的概率为",binom.pmf(3,4,0.25))
print("四道问题中答对四道的概率为",binom.pmf(4,4,0.25))假设四道四个选项的单项选择题,随便蒙,那么此时
四道问题中答对零道的概率为 0.31640625000000006
四道问题中答对一道的概率为 0.4218750000000001
四道问题中答对两道的概率为 0.21093750000000006
四道问题中答对三道的概率为 0.046875000000000035
四道问题中答对四道的概率为 0.003906250000000001
然后是累积概率,换句话说就是答对至少N道题的概率:
print("四道问题中至少一道的概率为",binom.cdf(1,4,0.25))四道问题中至少一道的概率为 0.73828125
四道问题中至少一道的概率为 4.0
期望与方差的语法与几何分布保持一致:
print(binom.var(4,0.25)) # 方差 Var(X) = npq
print(binom.mean(4,0.25)) # 均值,也就是期望E(X) = n * p
print(binom.std(4,0.25)) # 标准差
print(binom.expect(args=(4,0.25))) # 期望0.75
1.0
0.8660254037844386
1.0000000000000004
从上面看,想要答对四道题目都这么困难,看来以后还是不要侥幸了,好好学习才是王道。而下面我们还可利用scipy的类库计算一下我们参与“轮椅转转赢”比赛的获奖概率,这个游戏一共有五个问题,假如每个问题答对的概率都是0.25,那概率应该怎么计算呢?(原书P303的例题:)
print("最后一轮有五道题,每一道题的答对概率为0.25。")
print("那么答对两道题的概率为:{0:.3f}".format(binom.pmf(2,5,0.25)))
print("那么答对三道题的概率为:{0:.3f}".format(binom.pmf(3,5,0.25)))
print("那么答对两或三道题的概率为:{0:.3f}".format(binom.pmf(2,5,0.25) + binom.pmf(3,5,0.25)))
print("一道题都没答对的的概率为:{0:.3f}".format(binom.pmf(0,5,0.25)))
print("期望为:{0:.3f},方差为:{1:.3f}".format(binom.mean(5,0.25),(binom.var(4,0.25))) )最后一轮有五道题每一道题的答对概率为0.25。
那么答对两道题的概率为:0.264
那么答对三道题的概率为:0.088
那么答对两或三道题的概率为:0.352
一道题都没答对的的概率为:0.237
期望为:1.250,方差为:0.750
泊松分布
泊松分布在第七章中主要有两个用处:
1. 本身的用处,一种是根据一定时间内或一定区间内的平均次数,计算其他概率
2. 在n很大,p很小的情况下利用泊松分布代替二次分布进行计算
因为三种概率分布分布的语法是相近的,所以此处我们直接使用泊松分布计算书中的例题,也就是一个爆米花机问题,问一个一周平均发生3.4次故障的爆米花机下周会不会发生故障?拜托,如果我有一台一周发生3.4次故障的爆米花机,还决定下周不换的,那只有一个原因,那就是我傻了,emmmm,也有可能是我没钱。又或者我们是时候利用泊松分布计算一下蒙五十道题的概率了?
编程语法请参考原文档—>Scipy泊松分布
from scipy.stats import poisson
mu = 3.4
print("P309 爆米花机问题,一周内爆米花机平均发生故障:{0}".format(mu))
print("下一周爆米花机不发生故障的概率为:{0:.3f}".format(poisson.pmf(0, mu)))
print("下一周爆米花机发生三次故障的概率为:{0:.3f}".format(poisson.pmf(3, mu)))
print("其期望为:{0:.3f},方差为:{1:.3f}".format(poisson.mean(mu),(poisson.var(mu))) )P309 爆米花机问题,一周内爆米花机平均发生故障:3.4
下一周爆米花机不发生故障的概率为:0.033
下一周爆米花机发生三次故障的概率为:0.558
其期望为:3.400,方差为:3.400
mu_test = 0.05 * 50
print("P317 考试问题,每一道题的答对概率为:{0},我们用泊松分布来代替二次分布".format(mu_test))
print(“答对五题的概率为:{0:.3f}”。format(poisson.pmf(5,mu_test)))
print(“额外的:答对最多三题的概率为:{0:.3f }。“。format(poisson.cdf(3,mu_test)))P317考试问题,每一道题的答案概率为:2.5,
我们用泊松分布来 代替二次分布答对五题的概率为:0.067
额外的:答对最多三题的的概率为:0.758
参考资料
- Scipy二次分布参考地址
- scipy几何分布原文地址
- Scipy泊松分布
- 深入浅出统计学原书


 浙公网安备 33010602011771号
浙公网安备 33010602011771号