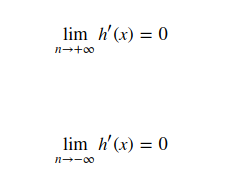Google提出的新型激活函数:Swish

简介

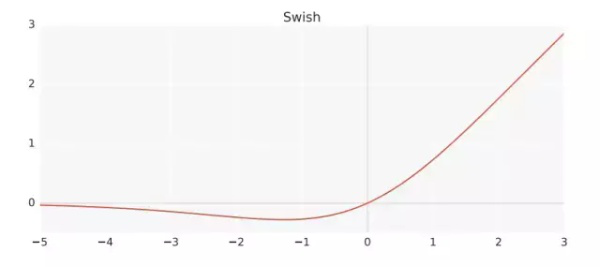
Swish是Google在10月16号提出的一种新型激活函数,其原始公式为:f(x)=x * sigmod(x),变形Swish-B激活函数的公式则为f(x)=x * sigmod(b * x),其拥有不饱和,光滑,非单调性的特征,而Google在论文中的多项测试表明Swish以及Swish-B激活函数的性能即佳,在不同的数据集上都表现出了要优于当前最佳激活函数的性能.

论文地址:https://arxiv.org/abs/1710.05941

详细讲述

激活函数常在神经网络中用于添加非线性因素,可以将激活函数定义为一个几乎处处可微的函数:h : R → R .[1].

激活函数存在饱和问题,当激活函数满足上述公式第一种情况时,称之为右饱和,反之为左饱和.

如果激活函数在非极限状态下存在一个常数C可以证明,在x大于或小于该常数C时,h(x)的一次导数存在恒等于零的情况时,则称h(x)为右硬饱和函数或左硬饱和函数.否则称其为软饱和函数.

因为反向传播算法的计算方式,可证明饱和激活函数会导致神经网络的性能大幅度下降.从而产生梯度消失问题,如常见的sigmod或tanh函数都存在该问题.

而现在深度神经网络中常用的激活函数为ReLU激活函数,其存在有上界,无下界,光滑的特点,其变种拥有在大多数数据集上的最佳性能.但是其变种复杂多样想要使用仍然存在很多的调试问题.而新的Swish函数则不同,其Swish-B形式在谷歌论文中的大型数据集即各种神经网络中中拥有绝对的优势,虽然现在还没有数学证明,但是其实践结果却可能意味着,我们之后再也不需要测试很多的激活函数了,这大大降低了我们的工作量.

Swish与ReLU一样有上界而无下界,但是其非单调性确与其他常见的激活函数不同,通知其也拥有平滑和一阶导数,二阶导数平滑的特性.

谷歌测试证明,Swich适应于局部响应归一化,并且在40以上全连接层的效果要远优于其他激活函数,而在40全连接层之内则性能差距不明显.但是根据在mnist数据上AleNet的测试效果却证明,Swich在低全连接层上与Relu的性能差距依旧有较大的优势.

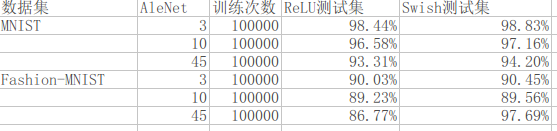
对于MNIST数据集而言,五层内的全连接层已经可以达到更好的测试性能,但是为了测试两种激活函数的不同,我使用了3,10,45三种不同的全连接层进行测试,同时为了加大数据集的难度,我同时使用了Fashion-MNIST数据集进行测试

测试结果:

总结.

google的论文告诉我们在更大的数据集与更深的神经网络上,Swish拥有更好的性能,而且当其与局部响应归一化结合使用时,味道更佳,但是我们在mnist与Fashion-MNIST数据集上的测试同时也表明,其实在部分中小型数据集上Swish激活函数,可能也拥有不错的性能表现.优于该函数没有数学证明,我们在使用时可能需要多实践一些.但是总体上我们可以认为,该激活函数是有效的.看来我们之后又多了一个炼丹的利器.

参考
[1] Noisy Activation Functions: Caglar Gulcehre, Marcin Moczulski
,Misha Denil, Yoshua Bengio.arXiv:1603.00391v3

[2] Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms. Han Xiao, Kashif Rasul, Roland Vollgraf. arXiv:1708.07747

[3] Swish: a Self-Gated Activation Function.Prajit Ramachandran, Barret Zoph, Quoc V. Leoc V. Le. arXiv:1710.05941