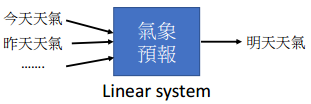
对于一个如下的线性系统
可通过Multiplication和Addition转换为线性方程租
即线性系统与线性方程租等价
线性系统的应用
大多数电路系统为线性系统
机器学习
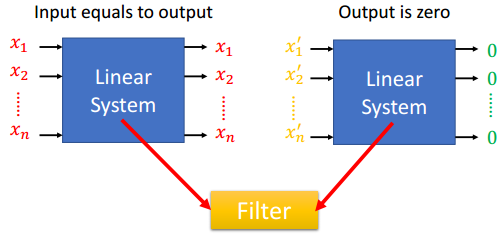
设计滤波器
通过特征值(Ei)与特征向量可以设计特定输出的线性系统
图像压缩
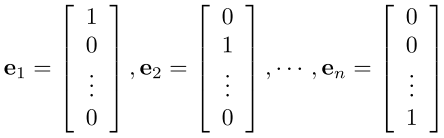
向量(Vectors)
向量的第i个元素为vi,v1=1, v2=2, v3=3
零向量
标准向量
向量集
包含n个元素的向量集为
![]()
R
n
矩阵(Matrix)
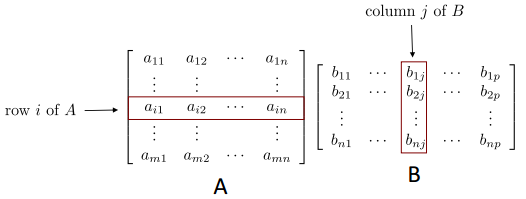
标记规则:先 Row 再 Column
零矩阵
单位矩阵(Identity matrix)
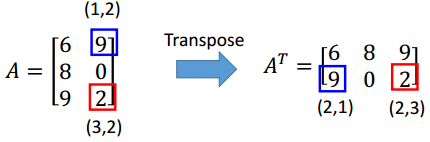
矩阵转置
AT中第(i,j)个元素为A中第(j,i)个元素
矩阵与向量
矩阵Am*n与向量x相乘结果为m维向量。可通过行角度和列角度理解:
eg.
A and B 都是mxn矩阵. 如果对于Rn中所有w,都有Aw = Bw. 那么A=B?
因为
线性组合(Linear Combination)
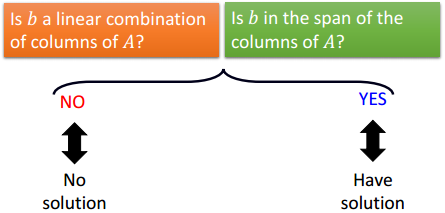
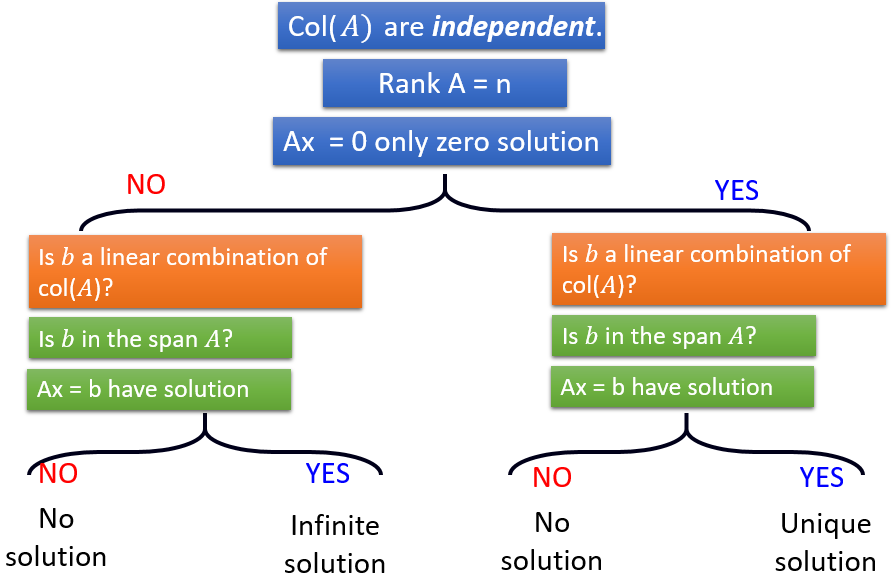
“Ax = b 是否有解” 可以转化为 “b是否是A中各列的线性组合”
线性空间(Span)
给定一组向量集合
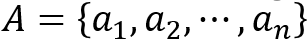
,Span A定义为其中各向量的所有线性组合,即
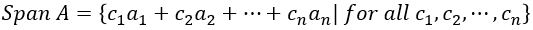
“Ax = b 是否有解”可以转化为 “b是否 ∈ Span A”
【总结】
对于
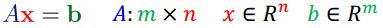
线性相关(Linear Dependent)
定义:给定一组向量集{a1, a2,..., an} ,若其中存在任一向量ai可由其他向量线性组合,则称该向量集线性相关
等价为如下
向量集{a1, a2,..., an} 线性相关:Ax = 0存在非零解
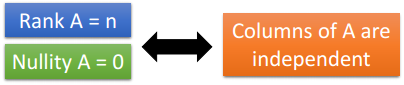
向量集{a1, a2,..., an} 线性独立:Ax = 0只有零解
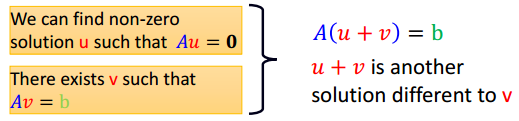
对于线性相关的向量集{a1, a2,..., an} / Ax = 0存在非零解 → 方程Ax=b只要有解,必有无穷多解
线性相关法证明:
齐次方程(Homogeneous Equations)Ax=0证明:
秩(Rank)
定义:矩阵中线性独立列的最大值
Nullity = Number of columns - rank
对于Am*n
【总结】
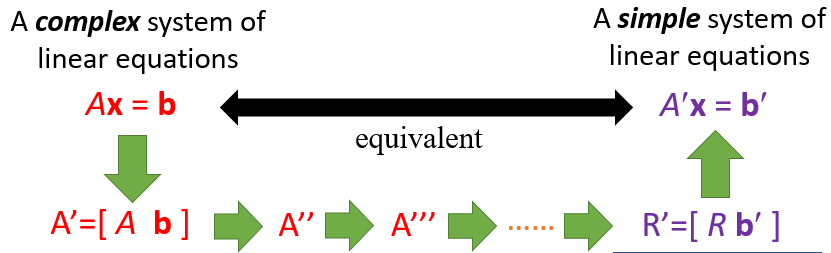
解线性方程方法
抽象为线性系统即为
其中A'=[A b]称为增广阵(augmented matrix)
R=[R' b']为简化行阶梯矩阵(reduced row echelon form,RREF)
- 矩阵是行阶梯型
- 含先导元素(leading entries)的列(pivot column)是标准向量
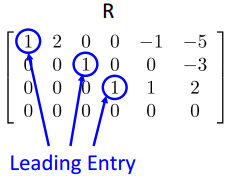
A'→R的变换称为基础行变换(elementary row operations)
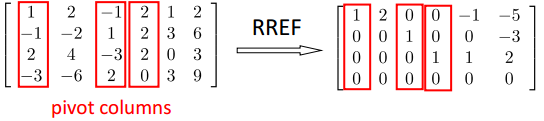
初始矩阵 v.s. RREF
列:关系不变、span 变化(即Col A≠Col R)
行:关系变化、span 不变(即Row A=Row R)
秩(Rank)
最大独立列的个数 = 主元列(Pivot Col)个数 = 非零行个数
由上可得,Rank A ≤ Min(列数,行数)
RREF与解的关系
对于瘦长型矩阵
若 Rank R = col A
无解:Rank R < Rank R'
唯一解:Rank R = Rank R'
若 Rank R < col A
无穷多解
对于扁平型矩阵
无解:Rank R < Rank R'
无穷多解:m = n 且 Rank R = Rank R'
唯一解:m < n 且 Rank R = Rank R'
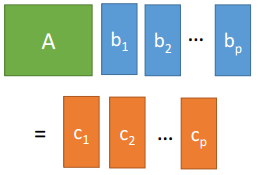
矩阵相乘的两个观点
内积
列的线性组合
AB = A[b1 b2 ... bp] = [Ab1 Ab2 ... Abp]
基础行变换与矩阵乘积
1. 互换
2. 缩放
3. 倍乘第i行、加至第j行
eg. A为m*n矩阵,其RREF为R,即
可逆
A为n*n矩阵,当且仅当以下条件成立时,A是可逆的:
- A的列张成(span)Rn
- 对所有b∈Rn, Ax=b都有解
- A的秩为n
- A的列相互独立
- Ax=0 只有零解
- A的nullity为0
- A的RREF为In
- 存在Bn*n使得BA = In
- 存在Cn*n使得AC = In
求解逆矩阵
对于An*n,将[A In]进行基础行变换,转化为[In B],则A-1=B
行列式(Determinants)
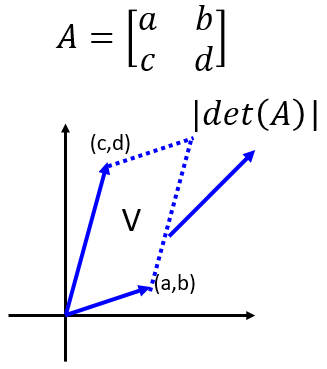
行列式的性质
- det(I) = 1
- 交换行改变det正负
- 行列式对每行都是线性
- det(AB) = det(A)det(B)
- a:det(A-1) = 1/det(A)
- b:det(A2) = det(A)2
行列式计算
选择某行
或者某列
其中cij为代数余子式(cofactor)
克拉默法则(Cramer's Rule)
C为A的代数余子阵,CT为A的伴随矩阵(adj A)
证明:
ACT = det(A)In
【注】A中row i与row j的代数余子式乘积为0,相当于A中row i与row j相同
子空间(Subspace)
一组满足以下条件的向量集V:
0向量 ∈ V
如果u,w ∈ V,则u+w ∈ V
如果u ∈ V,则cu ∈ V
零空间(Null Space)
定义:Null A={ v∈Rn:Av=0 }
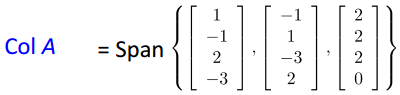
列空间(Column Space)
Col A={ Av:v∈Rn}
Row A=Col AT
11
基(Basis)
定义:基为子空间V的一个线性独立生成集
举例:矩阵列空间Col A的基为其先导列
【释】先导列相互独立;且其可生成Col A
基的性质
基是最小的生成集(generation set)
如果S为子空间V的生成集
Subspace V = Span S = Col S,即Col S的基与Subspace V相同,然而S的基为S的先导列(S的Subset),可参见上例
则V的基一定≤S的向量个数,即S可通过删去某些向量转化为V的基
基是子空间中最大的独立向量个数
子空间中的任何两个基包含相同个数的向量(即为子空间V的维度dim V)
此处证明较为抽象故省略,建立这种直觉即可
证明向量集S为子空间V的基
定义:基S为子空间V的一个线性独立生成集
线性独立:做RREF即可判断
生成集:已知dim V = k(通过RREF判断),而S是V的子集且含k个向量
eg.判断B是否为V的基。
满足以下两个条件,故B是V的基
- B中各向量独立
- dim V = 3,B∈V且含有3个向量
12
| |
维度 |
基 |
| Col A |
Rank A |
A的先导列 |
| Null A |
Nullity A
=n-Rank A |
Ax = 0的解向量 |
| Row A |
Rank A |
A的RREF中非零行 |
13
当满足以下条件时,一组向量集B可作为Rn的坐标系
坐标系B={u1,u2,...,un}为Rn空间的基
坐标系转换
其他系统↔笛卡尔坐标系
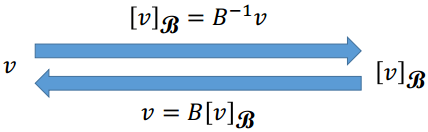
14
机器学习
15

16
秩的更多性质
已知Am×n、Bn×k,则Rank(AB) ≤ min(Rank(A), Rank(B))
证明
即证明以下两条同时成立
a. Rank(AB) ≤ Rank(A)
b. Rank(AB) ≤ Rank(B)
先证(a)
对可逆矩阵Qm×m,QA = R(RREF),因可逆矩阵是基础矩阵的乘积,初等行变换不会改变行空间,
即行空间的维度不会变化,即Rank不变,故有Rank(QA) = Rank(A)
Rank(AB) = Rank(QAB) = Rank(RB)
Rank(A) = Rank(PA) = Rank(R)
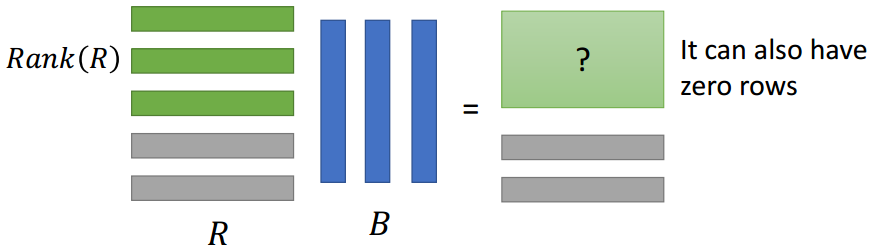
R中非零行即为Rank(R),而RB的非零行≤R中非零行,即Rank(RB) ≤ Rank(R),故有Rank(AB) ≤ Rank(A)
将(AB)T带入上式,可得Rank(AB) ≤ Rank(B),综上则有Rank(AB) ≤ min(Rank(A), Rank(B))
其他性质(证明省略)
- 若Rank(B) = n → Rank(AB) = Rank(A)
- 若Rank(A) = n → Rank(AB) = Rank(B)
- Rank(A+B) ≤ Rank(A) + Rank(B)
行列式的更多性质
交换行会改变行列式的正负
对每行来说,行列式是线性的
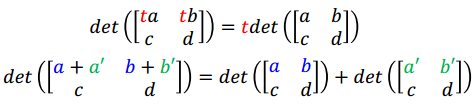
det(AB) = det(A)det(B)
det(A) = det(AT)
17
Av = λv(λ为特征值,v为特征向量【非零】)
可认为T(v) = Av,即对向量v的线性变换
即求解(A - λIn)v = 0
即λ对应的特征向量为Null(A - λIn),又称为λ的特征空间(eigenspace of λ)
判断λ是否为A的特征值?
即判断λ的特征空间尺寸,若为0 → 特征空间仅含{0} → 没有特征向量 → λ不是特征值
18 特征多项式
值t为方阵A的特征值
↔ 存在v ≠ 0 使得(A-tIn)v = 0
↔ (A-tIn)v = 0有多解
↔ (A-tIn)的列线性相关
↔ Rank(A-tIn) < n
↔ (A-tIn)不可逆
↔ det(A-tIn) = 0
特征多项式性质
相似矩阵有相同的特征多项式,即相同的特征值
证明如下
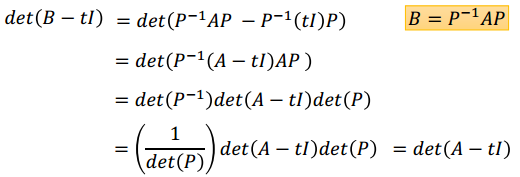
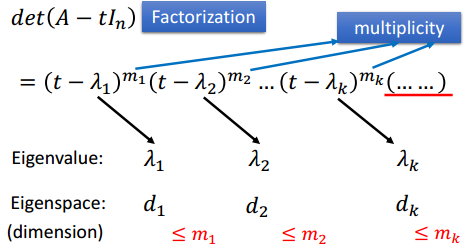
An×n的特征多项式次数为n
n个特征值(包含重根)之和 = A的迹
n个特征值(包含重根)之积 = A的行列式
(上下)三角阵的特征值为其对角元素
特征多项式与特征空间
19 对角化
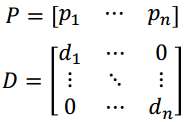
若A可对角化,即A = PDP-1
则AP = PD,即[ Ap1 ··· Apn ] = [ d1p1 ··· dnpn ]
pi即为A的特征向量,对应特征值为di
20 线性变换的对角化
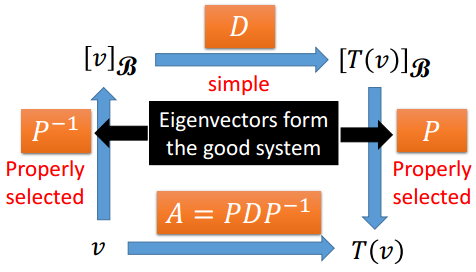
矩阵A可对角化条件
A的特征向量可组成Rn维基,即各特征向量相互独立
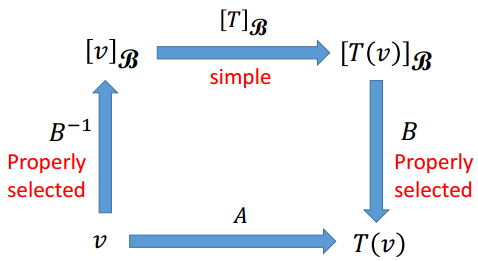
如下图,[T]B为B坐标系下的线性变换矩阵,找到合适的坐标系B可以得到较为简单的变换矩阵[T]B
21 正交化
范数Norm:
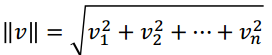
点乘:


22 正交投影
非零向量集S的正交补(Orthogonal Complement)记为S⊥,S⊥垂直于S中的每一个向量
S⊥ = { ν :v·u = 0 , all u ∈ S }
(Row A)⊥ = Null A
【释】
A = Span{a1 , a2},当且仅当a1·v = a2·v = 0时,v ∈ A⊥
即A⊥为“ Av = 0 ”的解,即为Null A
【注】
对Rn的任何子空间W,dimW + dimW⊥ = n
rank nullity
eg.W = Span{w1 , w2},w1 = [1 1 -1 4]T,w2 = [1 -1 1 2]T;W⊥ = Span{μ1 , μ2},w1 = [1 1 -1 4]T,w2 = [1 -1 1 2]T

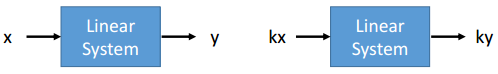
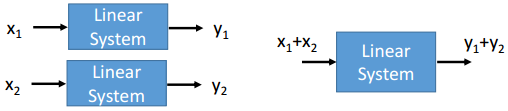

 :线性系统
:线性系统





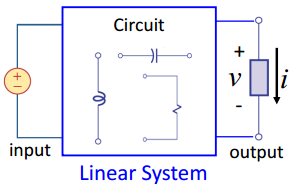
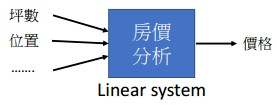


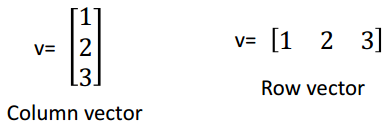
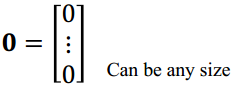
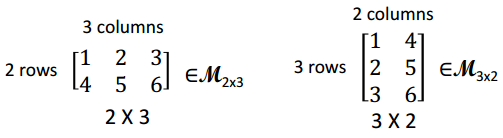
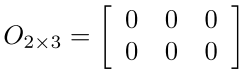
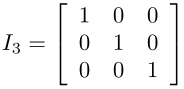


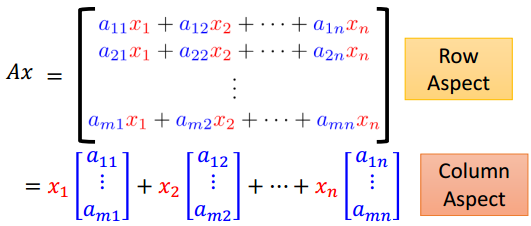
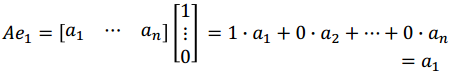
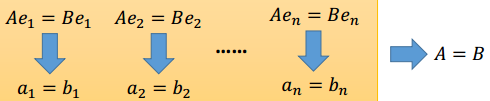
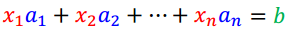
![]()

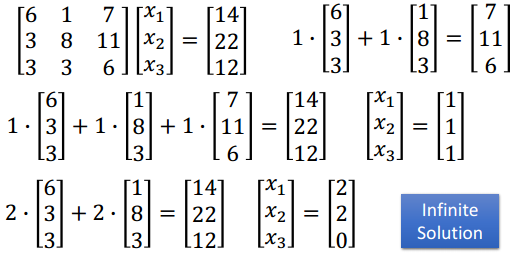
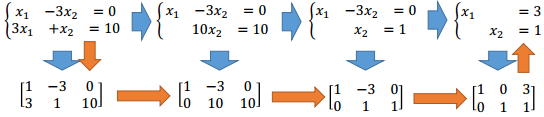



![]()
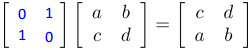
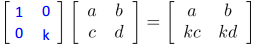
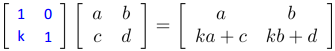
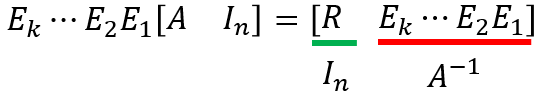


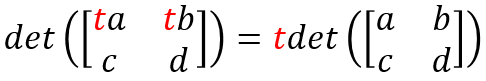
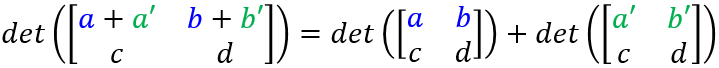
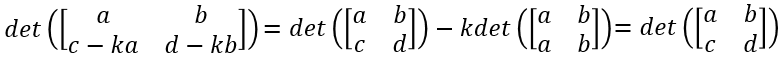
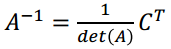


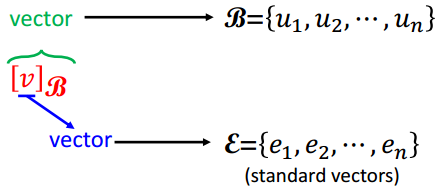
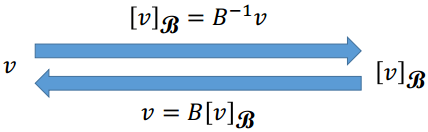


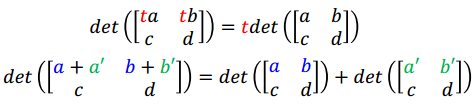
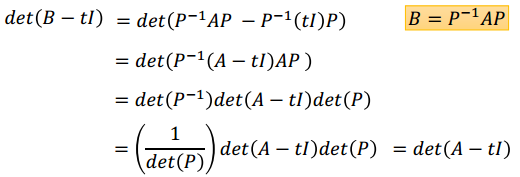

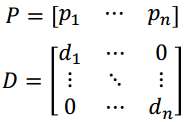


![]()
![]()


