古典密码之棋盘密码(ADFGVX,ADFGX,Polybius)

引言

棋盘密码只加密字母，不区分大小写（ADFGVX棋盘还可加密数字），若输入其它字符则原样保留。

若输入多行（段落），每行是单独加密的。
Polybius/ADFGX棋盘由于I/J在同一格，解密后需人工确认I和J。
ADFGX/ADFGVX棋盘原则上需要密钥二次加密，但可留空不使用密钥。若使用，则必须符合棋盘密码严格定义，即：
- Polybius/ADFGX明文只能是连续字母。
- ADFGVX明文只能是连续字母或数字或两者。
- Polybius密文必定是连续数字，且在1-5之间。
- ADFGX/ADFGVX密文必定是连续字母，且是ADFGX或ADFGVX。
- 密钥不能有重复字母！[后面会有一种密钥(偏移量,iv)可以有重复字母的算法]

[引用] 千千秀字 - 棋盘密码加密解密

例题

┌──────────────────────────────────────────┐
│                神奇的棋盘                  │
│                  300                     │
│    神奇的棋盘附有一张奇怪的纸条               │
│    请你发现蹊跷解密这个棋盘                  │
│                                          │
└──────────────────────────────────────────┘

Writeup（WP）

题目提供了一张图片

根据图片我们知道是ADFGVX密码。同时，二进制查看图片末尾存在隐藏字符：JRQXG5CLMV4XWWLVONQXS6LEON6Q====

>>> import base32
>>> print(base64.b32decode('JRQXG5CLMV4XWWLVONQXS6LEON6Q===='))
b'LastKey{Yusayyds}'

base32解密为：LastKey{Yusayyds}
2、一个文本文件dong.txt,内容如下：

>>> dong=[11,22,11,53,53,14,11,22,22,51,22,22,51,14,51,11,
      14,11,51,53,14,22,11,14,51,22,14,51,11,11,14,14,
      14,14,21,53,11,21,11,21,14,22,14,51,53,53,14,22,
      22,14,22,22,14,53,14,14,21,14,14,53,51,22,53,11,
      14,22,51,14,21,53,51,51,11,11,14,14,53,14,53,53,
      11,14,14,51,22,22,22,53,22,53,53,53,53,22,53,53,
      22,22,53,22,14,51,51,51,22,22,22,11,22,11,11,11,
      11,22,11,11,22,22,11,22,14,14,14,11,22,11,22,22,
      22,11,22,22,11,22,11,22,11,11,11,51,11,11,11,53,
      22,53,22,22,22,53,22,22,53,22,53,22,53,53,53,51]
'''print(set(dong)) #{11, 14, 51, 53, 22, 21}
 \  1  2  3  4  5
1   A B C D  E
2   F G H I/J K
3   L M N O P
4   Q R S T  U
5   V W X Y Z
'''
>>> m={11:'A',14:'D', 21:'F', 22:'G',51:'V', 53:'X'}
>>> cipher = ''.join([m[i] for i in dong])
>>> print(cipher)

此时尝试千千秀字的棋盘密码加密解密，提示：密钥不能有重复字母！
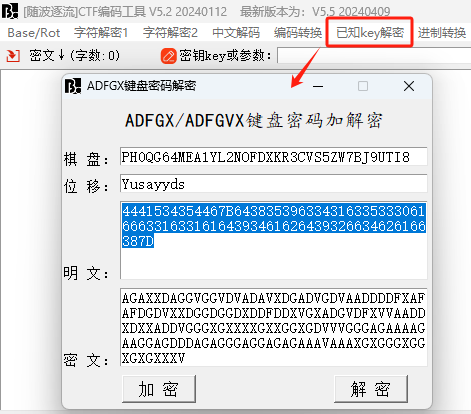
卡了几天，最后咨询了大佬，说是有一种带iv（偏移量）的密码，还推荐了[随波逐流]CTF编码工具，确实很牛！
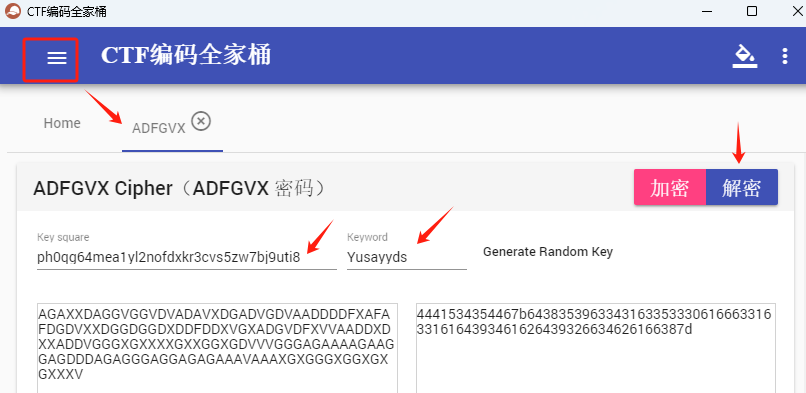
随波逐流有个大问题就是老是让升级，万一在断网的竞赛中，就不好了！后面发现CaptfEncoder也可以
想用Python实现这种带偏移量的棋盘密码解码，苦于找不到算法，大佬说逆向搞一下，我说github上有源码，对着js排除各种坑实现一版：

def  adfgvx_plus_decode(cp:str, kw:str, km:str)->str:
    '''
        cp:cipher         密文
        kw:keyword    密码
        km:keymap     键盘布局
    '''
    keyword = kw.lower()
    cipher = cp.lower()
    klen = len(keyword)
    clen = len(cipher) // klen 
    ncol = len(cipher) % klen
    #print(len(cipher),klen,clen,ncol)

    cols = ['']*klen
    i = j = k = 0
    while i<klen:    
        try: # js: string.charAt(j) 
            c = 'abcdefghijklmnopqrstuvwxyz'[j]
        except:
            c = ''
        t=keyword.find(c) # js: string.indexOf(c)     
        if t >= 0:
            col = clen + (1 if t < ncol else 0)
            cols[t] = cipher[k:k+col]
            k += col
            atmp = list(keyword)
            atmp[t] = '_'
            keyword = ''.join(atmp)
            i += 1
        else:
            j += 1
        #print(i,j,k,t,cols,keyword)

    s = ''
    for i in range(clen + 1):
        for j in range(klen):
            try:# js: string.charAt(j)
                s += cols[j][i]
            except:
                pass
            #print(s)

    a='adfgvx'
    return ''.join([km[a.find(s[i])*6+a.find(s[i+1])] for i in range(0,len(s),2)])

s=[['P','H','0','Q','G','6'],
   ['4','M','E','A','1','Y'],
   ['L','2','N','O','F','D'],
   ['X','K','R','3','C','V'],
   ['S','5','Z','W','7','B'],
   ['J','9','U','T','I','8']]
keymap=''.join([s[i][j] for i in range(6) for j in range(6)])
keyword = 'Yusayyds'
cipher = 'AGAXXDAGGVGGVDVADAVXDGADVGDVAADDDDFXAFAFDGDVXXDGGDGGDXDDFDDXVGXADGVDFXVVAADDXDXXADDVGGGXGXXXXGXXGGXGDVVVGGGAGAAAAGAAGGAGDDDAGAGGGAGGAGAGAAAVAAAXGXGGGXGGXGXGXXXV'
flag = adfgvx_plus_decode(cipher, keyword, keymap)
for i in range(0,len(flag),2):
    print(chr(int(flag[i:i+2],16)),end='')

flag

DASCTF{d859c41c530afc1c1ad94abd92f4baf8}

算法介绍

波利比奥斯方阵

公元前2世纪，一个叫Polybius的希腊人设计了一种将字母编码成符号对的方法。他使用了一个称为Polybius的校验表。Polybius校验表由一个5行5列的网格组成，网格中包含26个英文字母，其中I和J在同一格中。相应字母用数对表示。在古代，这种棋盘密码被广泛使用。Polybius校验表如下：

\	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	I/J	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	V	W	X	Y	Z

假设需要发送明文信息“Hello”，找到H对应2行3列，则加密为23，e加密为15，以此类推，得到密文：2315 31 31 34。

实际应用中，方阵中的字母顺序会被打乱，然后分发给信息发送方和接收方，增加第三方破解难度。
特点：

明文只能是字母；
密文全部为数字；
密文长度是明文的两倍，即偶数；
明文字母I和J的密文编码相同，解密后需人工确认。

ADFGX密码

1918年，第一次世界大战将要结束时，法军截获了一份德军电报，电文中的所有单词都由A、D、F、G、X五个字母拼成，因此被称为ADFGX密码。ADFGX密码是1918年3月由德军上校FritzNebel发明的，是结合了Polybius方阵和置换密码的双重加密方案。ADFGX密码之所以选择ADFGX一个字母，是因为它们译成摩斯密码时不容易混淆，可以降低传输错误的机率。ADFGX密码表如下：

\	A	D	F	G	X
A	b	t	a	l	p
D	d	h	o	z	k
F	q	f	v	s	n
G	g	i/j	c	u	x
X	m	r	e	w	y

这样加密的话Hello的密文就是：DD XF AG AGDF。

然后使用一个密钥将密文再次移位加密，得到最终密文。例如“hello”用ADFGX棋盘加密得到密文“DFAXFAFAFG”，然后用密钥“bye”再次加密：

b	y	e
D	F	A
X	F	A
F	A	F
G

密钥有几个字母，就有多少列，然后将密文一行一行填入。把密钥“bye”按字母顺序重排为“bey”，因此，密码不能有重复的字母,依照这个顺序将表格中的字母一列一列的抄写得到：DXFGAAFFFA，这就是最终密文。可见，由于增加了密钥，ADFGX棋盘的加密强度明显高于Polybius棋盘密码。
特点：

明文只能是字母；
密文只会是字母：ADFGX；
密文长度是明文的两倍，即偶数；
明文字母I和J的密文编码相同，解密后需人工确认。

ADFGVX密码

ADFGX密码发送含有大量数字的信息会有问题。在1918年6月，又加入一个字母V扩充，变成以6×6格共36个字符加密，这使得所有英文字母（不再将I和J视为同一个字）以及数字0到9都可混合使用。ADFGVX是被法国陆军中尉Georges Painvin所破解的:

\	A	D	F	G	V	x
A	w	h	e	n	2	g
D	o	9	3	a	b	c
F	d	f	i	j	k	l
G	m	p	q	r	s	t
V	u	v	x	y	z	0
X	1	4	5	6	7	8

例如“hello”用ADFGVX棋盘加密得到密文“DDAVDXDXFF”

然后用密钥“bye”再次加密：

b	y	e
D	D	A
V	D	X
D	X	F
F

依照“bey”的顺序抄写列，得到最终密文：DVDFAXFDDX。
特点：

明文只能是字母或数字或两者；
密文只会是字母：ADFGVX；
密文长度是明文的两倍，即偶数。

扩展

此外，类似的还有日历密码、普莱菲尔密码等；高级版的还有就是四面八方密码等；

上面给了带偏移量的棋盘密码解码，下面附上加密代码：

keySquare = 'ph0qg64mea1yl2nofdxkr3cvs5zw7bj9uti8'
keyword = 'yusayyds'.lower()
plaintext = "linux"
adfgvx = "ADFGVX"
ciphertext1 = ""

for i in range(len(plaintext)):
    index = keySquare.find(plaintext[i])
    ciphertext1 += adfgvx[index // 6] + adfgvx[index % 6] 
#print(ciphertext1,'FAXVFFXFGA')

colLength = len(ciphertext1) / len(keyword)
chars = "abcdefghijklmnopqrstuvwxyz"
ciphertext = ""
k = 0
for i in range(len(keyword)):
    while(k<26):
        t = keyword.find(chars[k])
        if t>=0:
            arrkw = list(keyword)
            arrkw[t] = '_'
            keyword = "".join(arrkw)
            break
        else:
            k+=1
    j=0
    while j < colLength:
        try:
            x=ciphertext1[j * len(keyword) + t]
        except:
            x=''
        ciphertext += x
        j+=1
print(ciphertext,'VXXFAAFGFF')

至此，其实还是不太明白这个带偏移量的棋盘密码的算法流程，今天晚了先欠下吧。

落之~

题外话：MARKDOWN中的表格单元格合并

合并行		c1
a2	合并列	c2
a3	合并列	c3
a4	大合并
a5	大合并

<table border=0 cellpadding=0 cellspacing=0 width=207 style='border-collapse:
 collapse;table-layout:fixed;width:156pt'>
 <col width=69 span=3 style='width:52pt'>
 <tr height=19 style='height:14.0pt'>
  <td colspan=2 height=19 class=xl636101 width=138 style='height:14.0pt;
  width:104pt'>合并行</td>
  <td class=xl156101 width=69 style='width:52pt'>c1</td>
 </tr>
 <tr height=19 style='height:14.0pt'>
  <td height=19 class=xl156101 style='height:14.0pt'>a2</td>
  <td rowspan=2 class=xl636101>合并列</td>
  <td class=xl156101>c2</td>
 </tr>
 <tr height=19 style='height:14.0pt'>
  <td height=19 class=xl156101 style='height:14.0pt'>a3</td>
  <td class=xl156101>c3</td>
 </tr>
 <tr height=19 style='height:14.0pt'>
  <td height=19 class=xl156101 style='height:14.0pt'>a4</td>
  <td colspan=2 rowspan=2 class=xl636101>大合并</td>
 </tr>
 <tr height=19 style='height:14.0pt'>
  <td height=19 class=xl156101 style='height:14.0pt'>a5</td>
 </tr>
 <![if supportMisalignedColumns]>
 <tr height=0 style='display:none'>
  <td width=69 style='width:52pt'></td>
  <td width=69 style='width:52pt'></td>
  <td width=69 style='width:52pt'></td>
 </tr>
 <![endif]>
</table>

posted @ 2024-04-19 23:11 folio 阅读(1251) 评论(0) 编辑收藏举报

刷新页面返回顶部

folio