2045. 到达目的地的第二短时间_2022_01_22

2045. 到达目的地的第二短时间

城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [u<sub style="display: inline;">i</sub>, v<sub style="display: inline;">i</sub>] 表示一条节点 u<sub style="display: inline;">i</sub> 和节点 v<sub style="display: inline;">i</sub> 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点，但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是  绿色 ，你 不能 在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

• 例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。

给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

• 你可以 任意次 穿过任意顶点，包括 1 和 n 。
• 你可以假设在 启程时 ，所有信号灯刚刚变成 绿色 。

示例 1：

       

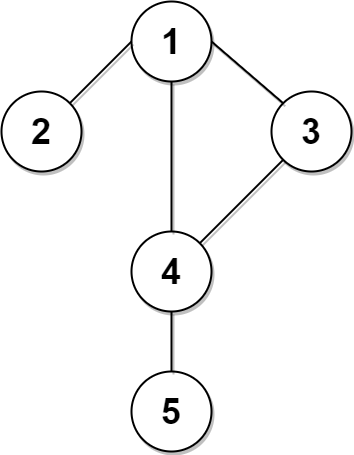
输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
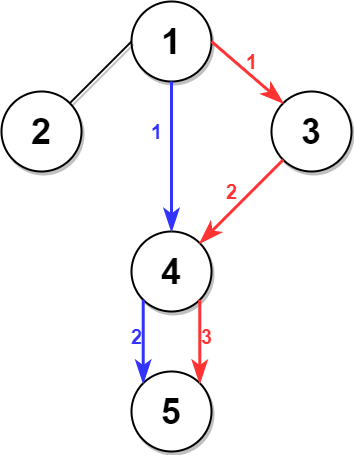
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。      

示例 2：

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

提示：

• 2 <= n <= 10<sup>4</sup>
• n - 1 <= edges.length <= min(2 * 10<sup>4</sup>, n * (n - 1) / 2)
• edges[i].length == 2
• 1 <= u<sub style="display: inline;">i</sub>, v<sub style="display: inline;">i</sub> <= n
• u<sub style="display: inline;">i</sub> != v<sub style="display: inline;">i</sub>
• 不含重复边
• 每个节点都可以从其他节点直接或者间接到达
• 1 <= time, change <= 10<sup>3</sup>

Solution

​func secondMinimum(n int, edges [][]int, time, change int) (ans int) {
    graph := make([][]int, n+1)
    for _, e := range edges {
        x, y := e[0], e[1]
        graph[x] = append(graph[x], y)
        graph[y] = append(graph[y], x)
    }

    // dist[i][0] 表示从 1 到 i 的最短路长度，dist[i][1] 表示从 1 到 i 的严格次短路长度
    dist := make([][2]int, n+1)
    dist[1][1] = math.MaxInt32
    for i := 2; i <= n; i++ {
        dist[i] = [2]int{math.MaxInt32, math.MaxInt32}
    }
    type pair struct{ x, d int }
    q := []pair{{1, 0}}
    for dist[n][1] == math.MaxInt32 {
        p := q[0]
        q = q[1:]
        for _, y := range graph[p.x] {
            d := p.d + 1
            if d < dist[y][0] {
                dist[y][0] = d
                q = append(q, pair{y, d})
            } else if dist[y][0] < d && d < dist[y][1] {
                dist[y][1] = d
                q = append(q, pair{y, d})
            }
        }
    }

    for i := 0; i < dist[n][1]; i++ {
        if ans%(change*2) >= change {
            ans += change*2 - ans%(change*2)
        }
        ans += time
    }
    return
}