集成学习的分类
bagging
从训练集从进行子抽样组成每个基模型所需要的子训练集,对所有基模型预测的结果进行综合产生最终的预测结果。
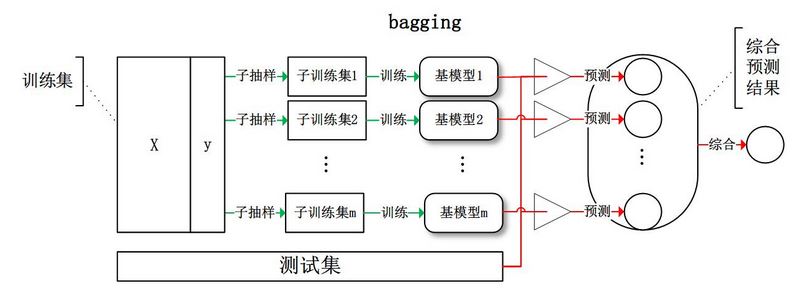
boosting
训练过程为阶梯状,基模型按次序一一进行训练(实现上可以做到并行),基模型的训练集按照某种策略每次都进行一定的转化。对所有基模型预测的结果进行线性综合产生最终的预测结果。
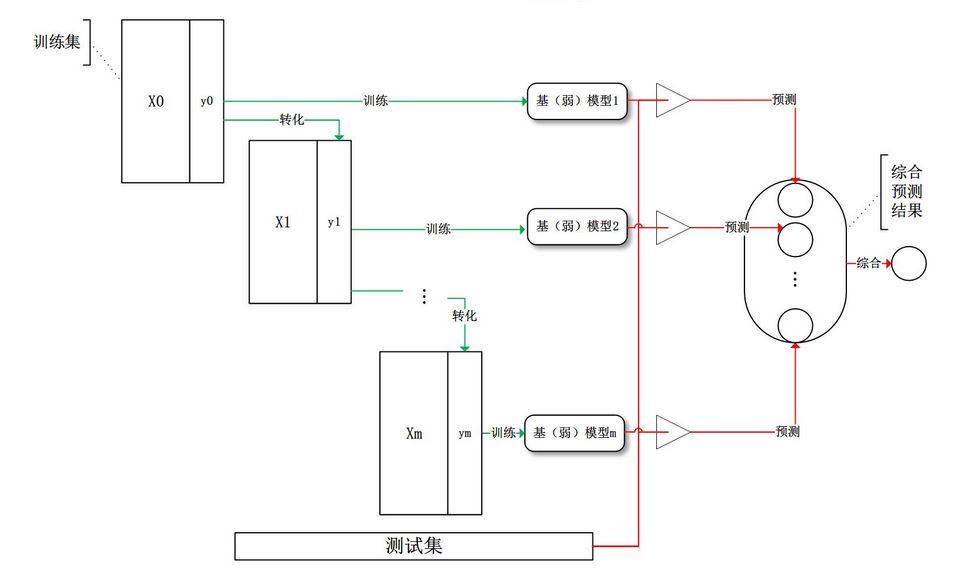
stacking
将训练好的所有基模型对训练基进行预测,第j个基模型对第i个训练样本的预测值将作为新的训练集中第i个样本的第j个特征值,最后基于新的训练集进行训练。同理,预测的过程也要先经过所有基模型的预测形成新的测试集,最后再对测试集进行预测。
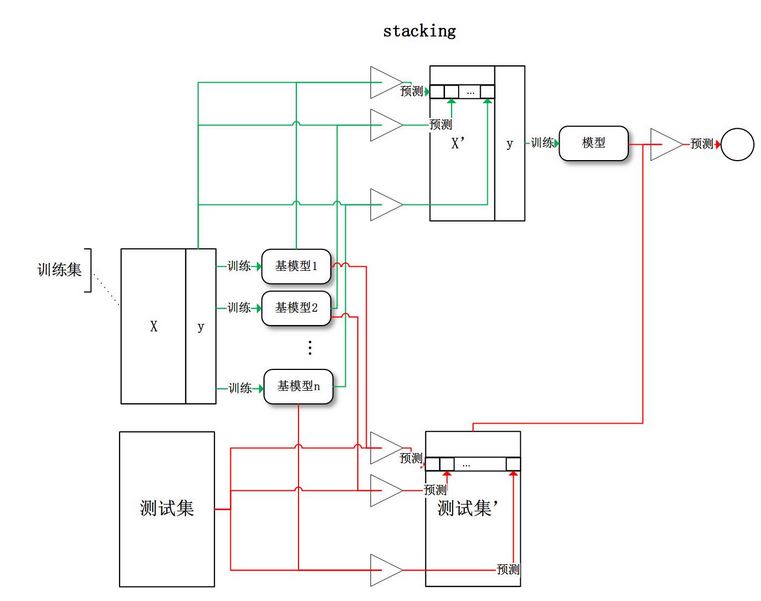
常见的集成模型
- 基于bagging的集成模型:随机森林
- 基于boosting的集成模型:AdaBoost、GBDT、XgBoost、LightGBM
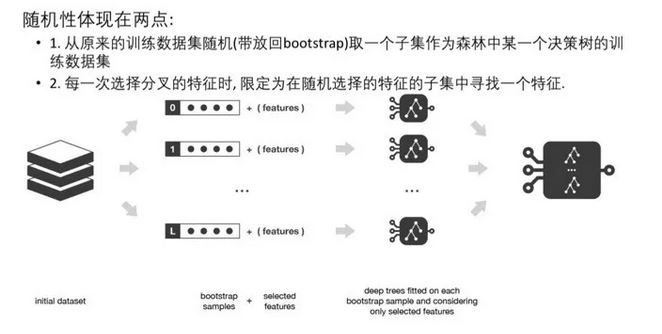
随机森林
随机森林=bagging + 决策树
同时训练多个决策树,预测时综合考虑多个结果进行预测。
优点
- 消除了决策树容易过拟合的缺点
- 减小了预测的方差,预测值不会因训练数据的小变化而剧烈变化。
AdaBoost
AdaBoost的思想是将关注点放在被错误分类的样本上,减小上一轮被正确分类的样本的权值,提高被错误分类的样本的权重。AdaBoost采用加权投票的方法,分类误差小的分类器权重大,分类误差大的分类器权重小。
AdaBoost算法流程
输入:
训练数据:\(T=\left\{ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})\right\}\),弱分类器个数\(M\)。其中\(x_{i} \in R^{n}\),\(y_{i} =+1,-1\)。
step1:
初始化训练样本权重分布:
\[D_{1}=(w_{11},w_{12},...,w_{1i}),w_{1i}=\frac{1}{N}
\]
step2:
对于\(m=1,2,...,M\)
- 使用具有权重分布\(D_{m}\)的训练数据集进行学习,得到弱分类器\(G_{m}(x)\)
- 计算\(G_{m}\)在训练集上的分类误差率:
\[e_{m}=\sum_{i=1}^{N}w_{m,i}I(G_{m}(x_{i})\neq y_{i})
\]
- 计算\(G_{m}\)在强分类器中所占比重:
\[\alpha_{m} =\frac{1}{2}log\frac{1-e_{m}}{e_{m}}
\]
- 更新训练数据集的权重分布:
\[w_{m+1,i}=\frac{w_{m,i}}{z_{m}}exp(-\alpha _{m}y_{i}G_{m}(x_{i})),i=1,2,...,N
\]
\[z_{m}=\sum_{i=1}^{N}w_{m,i}exp(-\alpha _{m}y_{i}G_{m}(x_{i}))
\]
step3:
得到最终分类器:
\[F(x)=sign(\sum_{i=1}^{N}\alpha _{m}G_{m}(x))
\]
GBDT
GBDT的全称为:Gradient Boosting Decision Tree,即梯度提升决策树。利用损失函数的负梯度拟合基学习器。
\[-\left [ \frac{\partial L(y_{i},F(x_{i}))}{\partial F(x_{i})} \right ]_{F(x)=F_{t-1}(x)}
\]
GBDT算法流程(回归)

GBDT算法流程(分类)

- 针对每个类别都先训练一个回归树,如三个类别,训练三棵树。比如对于样本\(x_{i}\)为第二类,则输入三棵树分别为:\((x_{i},0),(x_{i},1),(x_{i},0)\)。每棵树的训练过程就是CART的训练过程。这样对于样本\(x_{i}\)就得到了三棵树的预测值,然后用softmax来得到概率。
- 计算每个类别的残差,如类别1:\(\hat y_{i1} = 0-p_{1}(x_{i})\);类别2:\(\hat y_{i2} = 1-p_{2}(x_{i})\);类别3:\(\hat y_{i3} = 0-p_{3}(x_{i})\)
- 开始第二轮训练,针对第一类的输入\((x_{i},\hat y_{i1})\);第二类的输入\((x_{i},\hat y_{i2})\);第三类的输入\((x_{i},\hat y_{i3})\),继续训练三棵树。
- 重复第三步,直到迭代M轮。



