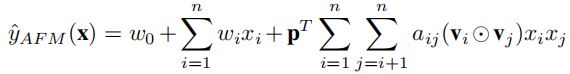
1 Deep Crossing——微软2016
文献来源:https://www.kdd.org/kdd2016/papers/files/adf0975-shanA.pdf
简介
一般机器学习任务需要人工进行特征工程,提取出对任务最有效的特征,在互联网时代,这种方式变的不再可取,越来越多的特征给人工特征工程带来了巨大的麻烦。对于文本或者类别特征而言,最常用的方式是转换为one-hot编码,但这种编码方式很难适用具有于大规模特征的任务,经过one-hot编码的特征想要进行高阶的特征组合,将会产生更高维的特征。Deep Crossing模型能够自动进行特征交叉,而且在进行特征交叉时并不想传统方式那样进行简单的拼接或者是相乘。Deep Crossing模型对dense特征和sparse特征分开处理,下面介绍模型的具体细节。
模型结构
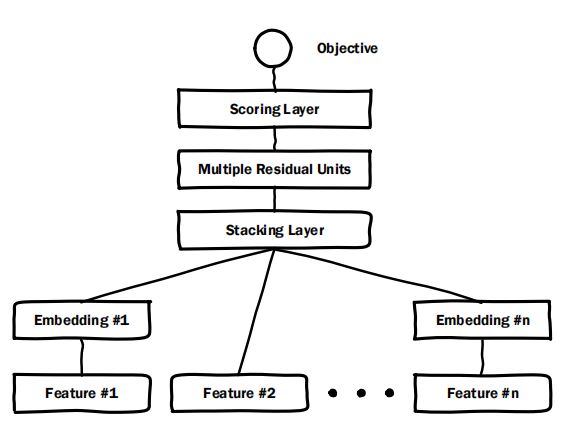
Deep Crossing模型主要包含四个模块,分别是:Embedding Layer、Stacking Layer、Residual Unit和Scoring Layer。
Embedding Layer
该层用于将高维稀疏的特征向量映射到低维稠密的向量,具体的实现是用单层全连接神经网络。
\(max()\)操作可以通过\(ReLU\)激活函数来实现。其中\(X^{I}_{j}\)是第\(j\)个输入特征,可以看出,每个特征都对应一个映射网络,它们之间的参数是独立的。
对于维度低于256的特征不需要进行转换,如图1中的Feature #2。
Stacking Layer
该层将Embedding Layer的输出拼接起来。
\(K\)表示输入特征数量。
Residual Unit
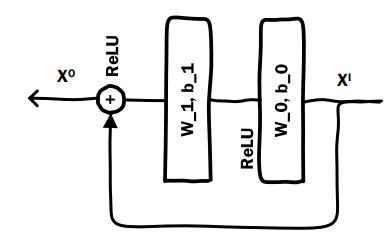
用公式表述为:
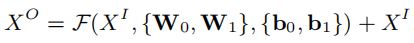
Scoring Layer
作为整个模型的输出,为了设计损失函数优化模型而存在的。
2 Wide&Deep——google2016
文献来源:https://arxiv.org/abs/1606.07792
模型结构
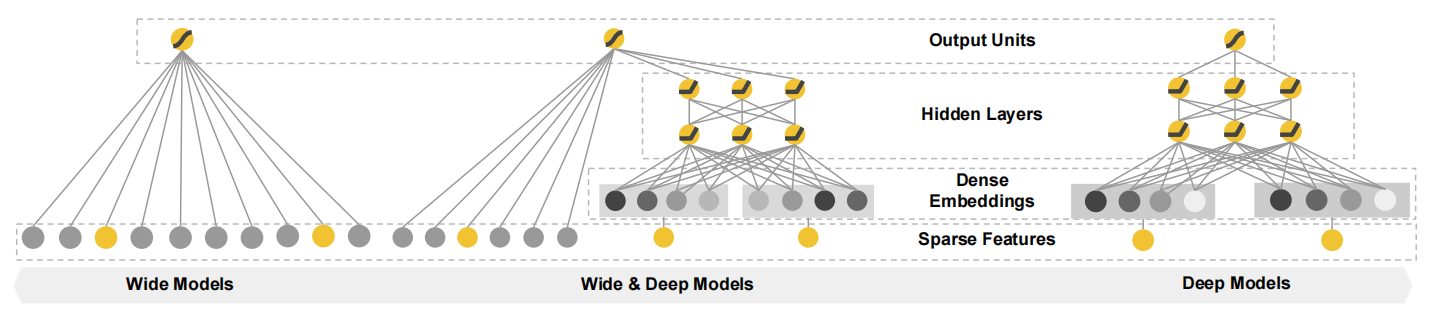
Wide&Deep模型如上图所示:其中左侧部分为Wide模型,最右侧部分为Deep结构,Wide&Deep是二者的结合。下面分别介绍各个不同的部分
Wide
Wide部分是一个线性模型,用数学公式表示为\(y=w^{T} \times x+b\),\(y\)是模型的输出结果,\(x\)是输入特征,是一个向量:\(x=[x_{1},x_{2},...,x_{d}]\)。输入特征包含两部分,一种是原始数据包含的特征,另外一种是经过特征转化之后得到的特征。最重要的一种特征转化方式就是交叉组合,交叉组合可以定义成如下形式:
这里的\(c_{ki}\)是一个bool型的变量,表示的是第\(i\)个特征的第\(k\)种转化函数\(\phi _{k}\)的结果。由于使用的是乘积的形式,只有所有项都为真,最终的结果才是1,否则是0。比如"AND(gender=female,language=en)"这就是一个交叉特征,只有当用户的性别为女,并且使用的语言为英文同时成立,这个特征的结果才会是1;再比如,第二个组合特征为:“AND(user_installed_app=netflix, impression_app=pandora)”,只有当一条记录的user_installed_app为netflix和impression_app为pandora时该组合特征才为1 通过这种方式我们可以捕捉到特征之间的交互,以及为线性模型加入非线性的特征。
Deep
Deep部分的模型细节如下图所示,模型输入是全部特征,对于连续的特征(如用户年龄、安装的APP数量等),直接输入到Deep中;对于类别型的特征需要进行编码之后再输入到Deep中。
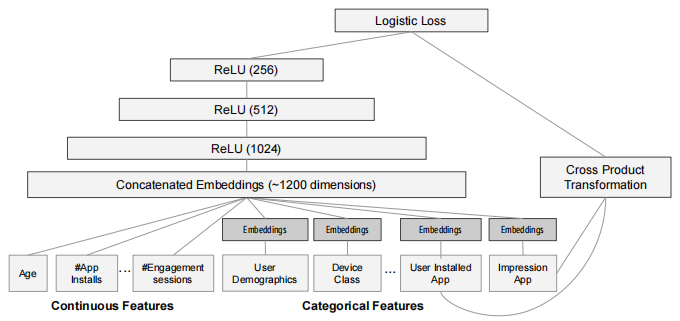
Wide&Deep
将Wide和Deep两部分合并到一起,最终模型输出为1的概率为:
其中\(a_{l_{f}}\)是Deep部分的最后一层输出。
代码实现
代码可直接运行,但本复现没有加入交叉积特征(因为实在不知道哪些特征适合交叉),数据集包含在项目中,与原始论文中不一样,谨慎参考
https://github.com/LUGANGo/Wide-Deep
3 DeepFM
文献来源:https://arxiv.org/abs/1703.04247
简介
简单线性模型,缺乏学习high-order特征的能力,很难从训练样本中学习到从未出现或极少出现的重要特征。FM模型可以通过点积和隐向量的形式学习交叉特征。由于复杂度的约束,FM通常只应用order-2的2重交叉特征。深层模型善于捕捉high-order复杂特征。现有模型用于CTR预估的有很多尝试,如CNN/RNN/FNN/PNN/W&D等,但都有各自的问题。FNN和PNN缺乏low-order特征,W&D需要人工构造Wide部分交叉特征。
本文提出的DeepFM模型是一种可以从原始特征中抽取到各种复杂度特征的端到端模型,没有人工特征工程的困扰。本文贡献如下:
- DeepFM模型包含FM和DNN两部分,FM模型可以抽取low-order特征,DNN可以抽取high-order特征。无需Wide&Deep模型人工特征工程。
- 由于输入仅为原始特征,而且FM和DNN共享输入向量特征,DeepFM模型训练速度很快。
模型结构
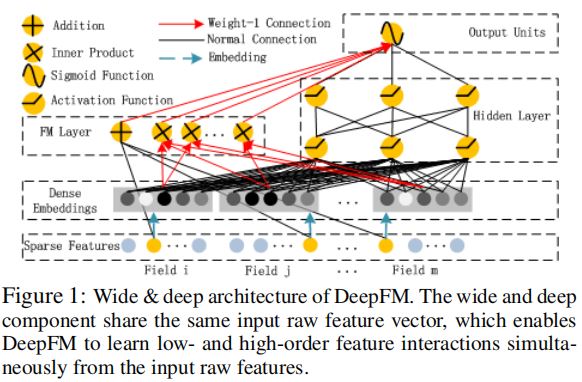
DeepFM模型结构如上图所示,包含因子分解机(FM)和全连接神经网络(Deep)两部分,这两部分的输入数据是共享的,模型采用联合训练的方式:
FM部分
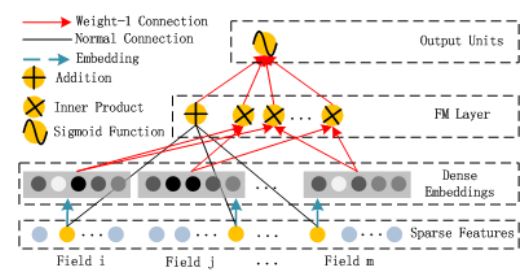
FM模型不但可以建模1阶特征,还可以通过隐向量点积的方法高效的获得2阶特征表示,即使交叉特征在数据集中非常稀疏甚至是从来没出现过。这也是FM的优势所在。模型的输入包含连续特征和离散特征,连续特征直接输入或者经过离散化,离散特征需要进行one-hot编码。
Deep部分
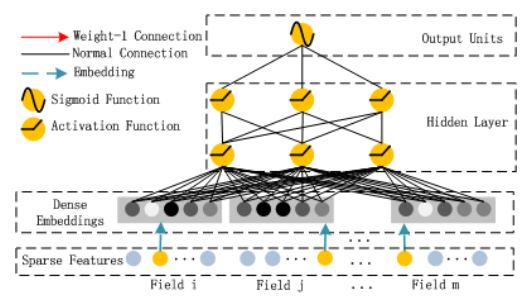
Deep部分是一个前馈神经网络,用于学习高阶特征交互。在输入特征部分,由于原始特征向量多是高纬度、高度稀疏、连续和类别混合的特征,为了更好的发挥DNN模型学习high-order特征的能力,文中设计了一套子网络结构(就是Dense Embeddings层),将原始的稀疏表示特征映射为稠密的特征向量。
子网络结构
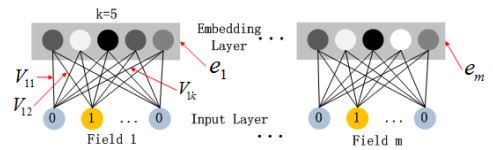
子网络设计时的两个要点:
- 不同field特征长度不同,但是子网络输出的向量需具有相同维度;
- 利用FM模型的隐特征向量V作为网络权重初始化来获得子网络输出向量。所有特征转成的embedding向量拥有相同的维度k。并且和FM模型当中的维度也是一样的,并且这个embedding的初始化也是借用FM当中的二维矩阵V来实现的。我们都知道V是一个d x k的二维矩阵,而模型原始输入是一个d维的01向量,那么和V相乘了之后,自然就转化成了k x 1的embedding了。
这里的第二点可以这么理解,如上图假设k=5,对于输入的一条记录,同一个field只有一个位置是1,那么在由输入得到dense vector的过程中,输入层只有一个神经元起作用,得到的dense vector其实就是输入层到embedding层该神经元相连的五条线的权重,即vi1,vi2,vi3,vi4,vi5。这五个值组合起来就是我们在FM中所提到的Vi。文中将FM的预训练V向量作为网络权重初始化替换为直接将FM和DNN进行整体联合训练,从而实现了一个端到端的模型。
4 Deep&Cross——google2017
文献来源:https://arxiv.org/abs/1708.05123
模型结构
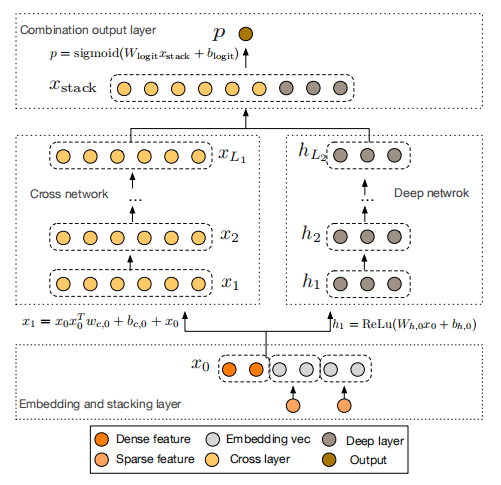
Deep&Cross和Deep&Wide模型的不同之处主要在于Cross部分,其他部分比较相似,模型结构如上图所示,分为Embedding layer、Cross Network、Deep Network和Combination layer四部分。
Embedding layer
该层的主要目的是将稀疏的类别特征进行嵌入,然后和稠密类特征拼接起来,作为后续模块的输入。原文中对dense特征和sparse特征的处理有一些小trick;对于dense类的特征取对数(log)进行归一化;对于sparse类的特征编码方式为:假设某个类别特征的取值个数为\(k\),那么该类别特征将被Embedding成维度为\(6\times k^\frac{1}{4}\)的稠密特征。
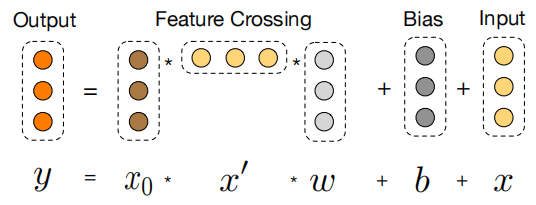
Cross Network
Cross部分引入了残差结构。可以使交叉的层数更深。每一层的计算公式如下:
\(x_{0}\)是Embedding layer得到的嵌入向量。
Deep Network
该部分就是普通的全连接神经网络。
Combination layer
该部分将Cross部分和Deep部分的输出拼接起来,用逻辑回归模型做最终点击率的估计。
5 DIN
文献来源:https://arxiv.org/abs/1706.06978
简介
近年来,基于深度学习的点击率预估技术已经得到了长足的发展,由于特征的稀疏性,为了更好地利用深层神经网络的拟合非线性能力、降低计算开销,目前的方法都是将稀疏、高维的特征进行编码,变成稠密、低维的特征向量,特征编码通常都是利用线性映射来实现的,给定一个用户或者是商品,其特征经过映射后拼接在一起输入到神经网络模型中进行点击率估计。该方法的缺点是,前面所述的嵌入是对特征的编码,只要给定一个特征组合,那么编码后的特征向量是为一个,按照这种编码方式,用户被编码成长度固定的特征向量,无论该用户之前的购买行为是什么。然而实际并不是这样的,对于一个特定商品,用户是否会购买(或点击)取决于其历史购买(或点击)的商品于该商品的相关程度,相关度大的历史购买行为对用户特征的刻画更有利,而相关度小的历史购买行为对用户特征的贡献可以忽略。本文提出的深度兴趣网络(DIN)可以根据用户的历史购买行为序列(其实就是商品)动态地生成该用户的特征向量。在工程实现方面,该文还设计了独特的训练方式,使得DIN模型在大规模数据上能够得以落地。
Base Model
在介绍DIN模型之前,我们先来看看一般的处理方法。我们的目标是估计用户是否会点击某个商品,因此输入包含用户特征、用户的历史购买商品、候选商品,为了结果的准确性,通常还要输入用户的上下文特征。第一步我们需要对特征进行编码,假定某个商品有\(m\)个特征,每个特征有\(k_{i}\)个取值,那么我们需要对\(\sum_{i=1}^{m}k_{i}\)个特征值进行编码。对所有的用户历史购买商品编码之后在进行池化,接着与用户自身的特征编码、候选商品的特征编码等拼接在一起,然后输入到深层神经网络中。
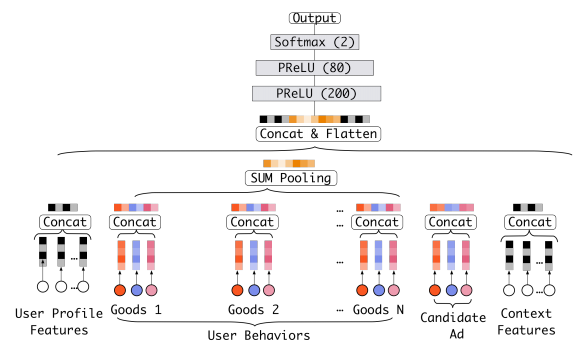
从上面描述的点击率预估过程可以看到,用户的特征并不会随着其历史购买行为的变化而发生改变,但实际上考虑用户的动态变化的兴趣对于估计该用户对某个商品点击与否是很有必要的。因此DIN模型正是在整体架构和计算过程不变的情况下考虑了这一点。
DIN Model
具体地,DIN计算用户的历史购买商品与当前候选商品的相关性得分(可以认为是一种注意力机制),该得分当作历史购买商品的权重。
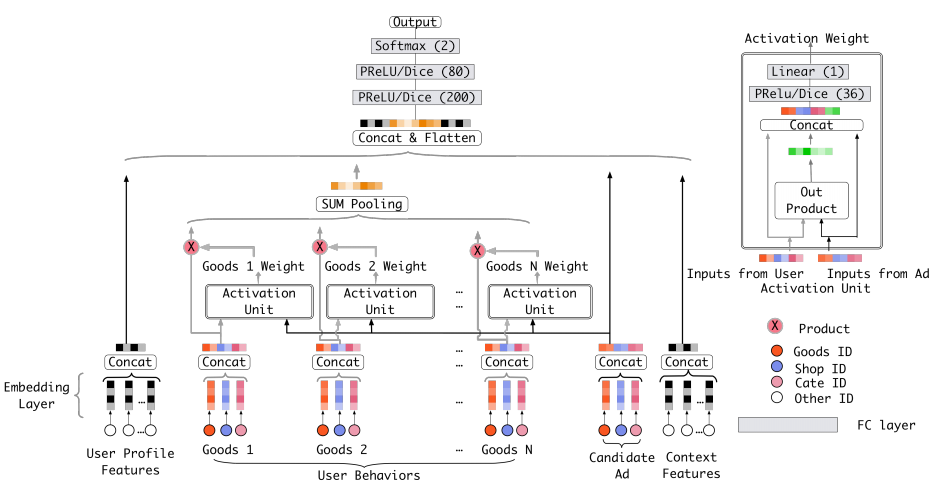
用数学公式描述为:
其中\(\left\{ \textbf{e}_{1},\textbf{e}_{2},...,\textbf{e}_{H}\right\}\)是用户\(U\)的历史购买的\(H\)个商品的嵌入向量;\(\textbf{v}_{A}\)是当前候选商品的嵌入向量;\(a()\)用于计算两个输入向量的相关性,具体结构如上图右边部分所示,较为简单,不做介绍。
6 NFM
文献来源:http://staff.ustc.edu.cn/~hexn/papers/sigir17-nfm.pdf
简介
许多预估任务需要对类别变量(如用户ID、性别职业等人口属性特征)进行建模。为了应用标准的机器学习技术,类别变量总是通过one-hot编码转换为二值化特征的集合,导致特征向量高度稀疏。为了有效的从稀疏数据中学习,解释特征间交互是至关重要的。
FM模型是一种流行的解决方案,它使用二阶特征交互。然而,FM模型的特征交互是一种线性的方式,不能充分的捕获真实数据中的非线性和复杂的固有结构。随着深度神经网络(如Wide&Deep、DeepCross)在工业界逐步用于学习非线性特征交互,网络结构也变得更加难以训练。
NFM将FM模型(用于建模二阶特征交互)的线性和神经网络(用于建模高阶特征交互)的非线性结合在一起。从概念上讲,NFM比FM更具有表达能力,因为FM可看作没有隐藏层的NFM的特例。NFM通过在神经网络建模中设计了一种新的操作:Bilinear Interaction(Bi-Interaction) pooling。通过在Bi-Interaction层上堆砌非线性层,能够加深浅层的线性FM,用来建模更高阶和非线性的特征交互关系,有效的提升FM的表达力。传统的深度学习方法通常在低层次上拼接或求平均嵌入向量,Bi-Interaction pooling的使用可以编码更多的特征交互,极大的促进了“deep layers”学习更有意义的信息。
NFM数学描述
公式的前两部分与矩阵分解模型的线性部分一样,是线性回归模型。关键在于\(f(\textbf{x})\)的设计。
\(f(\textbf{x})\)模型结构
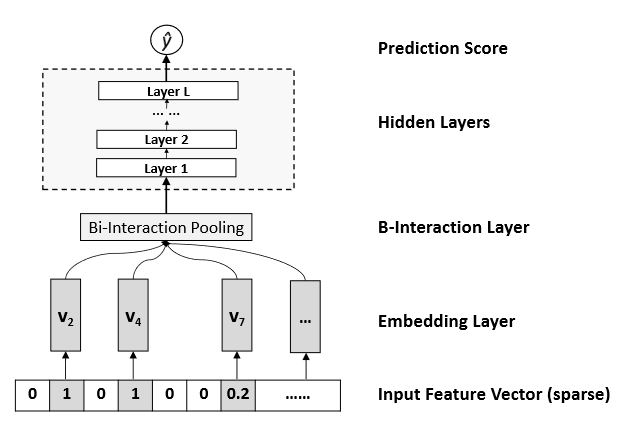
Embedding Layer
该层是一个全连接神经网络,将每个特征映射到一个稠密且低维的向量\(v_{i}\),将原始特输入的征值\(x_{i}\)乘以其对应的\(v_{i}\)便可得到转换后的嵌入向量集合\(\textbf{v}_{x}=\left\{ x_{1}v_{1},x_{2}v_{2},...,x_{n}v_{n}\right\}\)。
Bi-Interaction Layer
该层的主要目的是将Embedding Layer得到的嵌入向量集合\(\textbf{v}_{x}\)变换成一个向量,在这个过程中需要进行两两向量的特征交互。
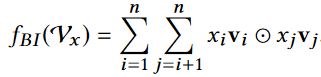
优点:实现特征交互的同时不需要引入额外的需要学习的参数
Hidden Layers和Prediction Score部分比较常规,不做介绍
7 AFM
文献来源:https://arxiv.org/pdf/1708.04617.pdf
简介
因子分解机(FMs)是一种有监督学习方法,通过结合二阶特征交互作用来增强线性回归模型。尽管FM有效,但它平等的看待各种特征交互,这限制了模型的能力,因为并非所有特征交互都同样有用和具有预测性。例如,与无用特性的交互甚至可能引入噪声并对性能产生不利影响。该文利用注意力机制识别有用的特征交互,能有效提升FM模型的性能。
模型结构
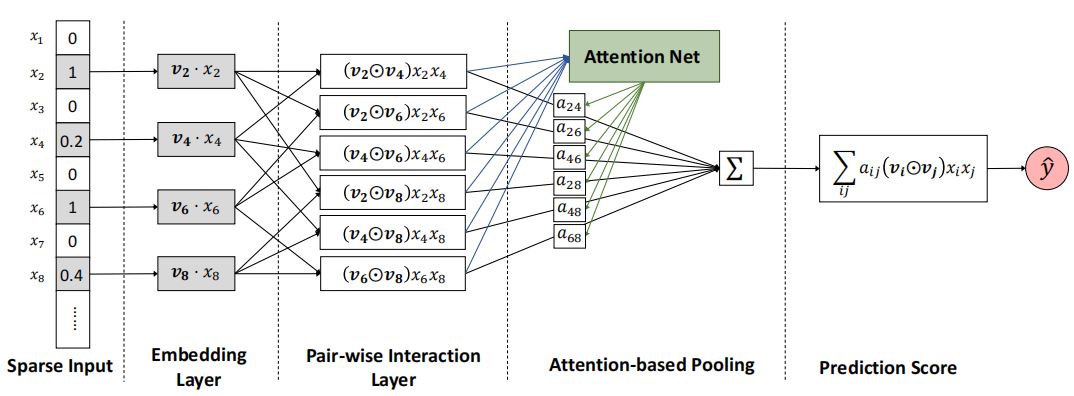
Sparse Input
该部分就是原始的稀疏输入数据。
Embedding Layer
该层对输入数据进行嵌入,每个特征都有一个对应的嵌入向量\(\textbf{v}_{i}x_{i}\)。其中\(\textbf{v}\)是可学习的参数。
Pair-wise Interaction Layer
该层对所有的非零嵌入向量进行两两交互,假设有\(m\)个特征,则共产生\(m(m-1)/2\)个交互向量。

Attention-based Pooling
该层为每一个交互特征向量分配一个注意力分数,使得模型能够有区分地对待各个交互,提升模型的性能。该层的输出可表示如下:
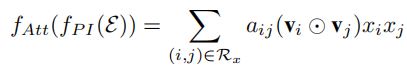
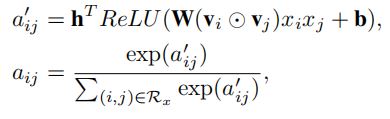
\(\textbf{h}\)、\(\textbf{W}\)和\(\textbf{b}\)是注意力网络的参数。
Prediction Score