DSSM模型——Learning Deep Structured Semantic Models for Web Search using Clickthrough Data

本文是2013年微软发表的论文的简要回顾，文中采用深层神经网络结构来学习查询（query）和文档（document）的隐式特征表示，然后用cosine函数计算两者之间的相似性
全文地址如下：https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/cikm2013_DSSM_fullversion.pdf

论文首先分析了已有的语义分析模型的缺点：

• LSA、PLSA、LDA，但是因为他们采用的都是无监督的学习方法，因此在实际的场景中表现的并不好。
• 通过用户查询和点击序列进行建模的BLTMs和DPMs，BLTMs不仅要求共享主题分布，而且还给每个主题分配相似的词组；DPMs则使用S2Net算法并结合LTR中的piarwise方法。在实验中他们的效果表现要比LSA、PLSA、LDA效果好。然后虽然BLTMs使用了点击数据进行训练，但其使用的是最大似然方法优化目标，该方法对于排序来讲并不是最优的。DPMs则会产生一个巨大的稀疏矩阵，虽然可以通过删除词汇减小维度，但相应的效果也会减弱
• 结合深度自编码的方法，虽然表现较传统的LSA效果好，但由于其采用的是无监督的学习方法，模型参数的优化是基于重建文档，而不是区分相关性，因此基于深度自编码的方法在效果上并没有显著优于关键词匹配。

DSSM模型

模型架构

图1 DSSM模型结构

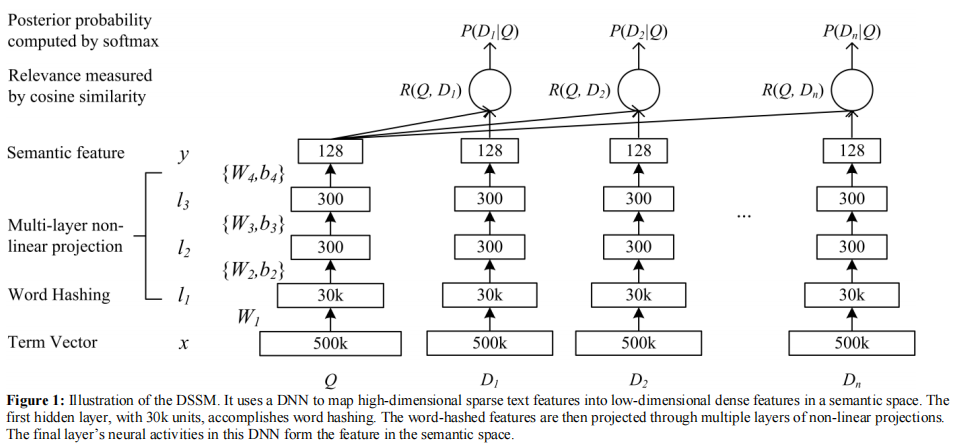
\(\quad\)模型采用的是典型的“双塔模式”——查询（query）塔和文档（document）塔，后来推荐系统领域的很多算法模型采用的也是这种双塔模式。
\(\quad\)对于某个查询（query），通过Bag-Of-Words可以得到其原始特征向量，文中将所有的query和document的特征向量都固定为500k的维度，这个特征向量称为Term Vector。由于原始的Term Vector很长，因此在输入MLP前需要进行维度压缩，与一般降维方法不同的是，文中采用“word hashing”技术，将Term Vector压缩为30k维的向量，然后在输入到MLP中，用于学习该query的最终隐式特征向量。对于某个document，获得其隐式特征向量的方式与query的处理方式一样。

数学描述

用\(x\)代表输入的Term Vector，\(y\)代表模型的输出（query或document的隐式特征表示），\(l_{i},i=1,2...N-1\)表示MLP的第\(i\)个隐藏层，\(W_{i}\)表示第\(i\)层的权重，\(b_{i}\)表示第\(i\)层的偏置。则有：

\[l_{1}=W_{1}x \]

\[l_{i}=f(W_{i}l_{i-1}+b_{i}),i=2,2,...N-1 \]

\[y=f(W_{N}l_{N-1}+b_{N}) \]

式中\(f\)表示激活函数，文中用tanh。
最后某个查询（query）\(Q\)和某个文档（document）\(D\)的相似性按如下公式计算：

\[R(Q,D)=cosine(y_{Q},y_{D})=\frac{y_{Q}^{T}\cdot y_{D}}{\left \| y_{Q} \right \|\left \| y_{D} \right \|} \]

Word Hashing

word hashing基于n-gram模型，其目的是对bag-of-words得到的term vector进行降维。以单词good为例，说明word hashing是怎样操作的。

• 对good的首尾分别添加标志位"#"，得到#good#
• 对#good#进行n-gram分割。当n=3时，得到#go、goo、ood、od#，于是可以用这四个词表示good这个词

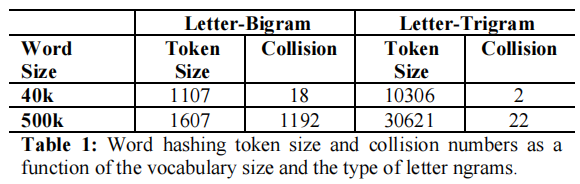
此外，文中还分析了产生冲突的情况，即不同的单词经过word hashing之后会得到相同的结果。由表中的结果可以看到，产生冲的的概率是很小的。

word hashing的代码实现

import itertools
import numpy as np
import re
import collections


def gen_trigrams():
  """
      Generates all trigrams for characters from `trigram_chars`
  """
  trigram_chars="abcdefghijklmnopqrstuvwxyz"
  t3=[''.join(x) for x in itertools.product(trigram_chars,repeat=3)] #len(words)>=3
  t2_start=['#'+''.join(x) for x in itertools.product(trigram_chars,repeat=2)] #len(words)==2
  t2_end=[''.join(x)+'#' for x in itertools.product(trigram_chars,repeat=2)] #len(words)==2

  trigrams=t3+t2_start+t2_end
  vocab_size=len(trigrams)
  trigram_map=dict(zip(trigrams,range(1,vocab_size+1))) # trigram to index mapping, indices starting from 1
  return trigram_map


def sentences_to_bag_of_trigrams(sentences):
  """
      Converts a sentence to bag-of-trigrams
      `sentences`: list of strings
      `trigram_BOW`: return value, (len(sentences),len(trigram_map)) size array
  """
  trigram_map=gen_trigrams()
  trigram_BOW=np.zeros((len(sentences),len(trigram_map))) # one row for each sentence
  filter_pat = r'[\!"#&\(\)\*\+,-\./:;<=>\?\[\\\]\^_`\{\|\}~\t\n]' # characters to filter out from the input
  for j,sent in enumerate(sentences):
      sent=re.sub(filter_pat, '', sent).lower() # filter out special characters from input
      sent=re.sub(r"(\s)\s+", r"\1", sent) # reduce multiple whitespaces to single whitespace
      words=sent.split(' ')
      indices=collections.defaultdict(int)
      for word in words:
          word='#'+word+'#'
          #print(word)
          for k in range(len(word)-2): # generate all trigrams for word `word` and update `indices`
              trig=word[k:k+3]
              idx=trigram_map.get(trig, 0)
              #print(trig,idx)
              indices[idx]=indices[idx]+1     
      for key,val in indices.items(): #covert `indices` dict to np array
          trigram_BOW[j,key]=val
  return trigram_BOW



if __name__ == "__main__":
  sentences = ['my name is degnl', 'I am from abcd']
  trigram_BOW = sentences_to_bag_of_trigrams(sentences)
  print(trigram_BOW[0])
  print(len(trigram_BOW[0]))

模型学习

首先，通过softmax函数从它们之间的语义相关性得分中计算给定查询的文档的后验概率：

\[P(D|Q)=\frac{exp(\gamma R(Q,D))}{\sum _{D^{'}\in D}exp(\gamma R(Q,D^{'}))} \]

其中\(\gamma\)表示平滑因子，和训练集测试集的划分有关。理论上，\(D\)应包含全体文档，但作者进行了近似采样，即\(D=D^{+} \cup D^{-}\) 。其中\(D^{+}\)表示与某个查询相关的文档，\(D^{-}\)表示与某个查询不相关的文档，文中随机采样了4个不相关文档。

在训练中，模型参数应当使得与某个查询相关的文档的可能性最大化。即我们需要最小化以下损失函数：

\[L(\Lambda )=-log\prod_{(Q,D^{+})}^{}P(D^{+}|Q) \]

参考

• 论文｜从DSSM语义匹配到Google的双塔深度模型召回和广告场景中的双塔模型思考
• DSSM (Deep Semantic Similarity Model) - Building in TensorFlow