BPR: Bayesian Personalized Ranking from Implicit Feedback

个性化排序的任务是为用户提供一个项目的排序列表。这也被称为项目推荐。一个例子是一个在线商店，它希望推荐一个用户可能想要购买的个性化商品排名列表。在本文中，我们研究了必须从用户的内隐行为（例如，过去的购买）中推断出排名的场景。关于隐式反馈系统，有趣的是，只有积极的观察结果可用。未观察到的用户项目对，例如用户尚未购买项目，是真正的负面反馈（用户对购买项目不感兴趣）和缺失值（用户可能希望在将来购买项目）的混合物。

问题定义

\(U\)和\(I\)分别是用户和商品的集合，在推荐任务中只有隐式反馈\(S\subseteq U \times I\)可用。推荐系统的任务是为用户提供个性化的总排名\(>_{u} \subset I^{2}\)，其中\(>_{u}\)必须满足如下性质：

• 整体性：\(\forall i,j\in I: i\neq j\Rightarrow i >_{u} j \cup j >_{u} i\)
• 反对称性：\(\forall i,j\in I: i >_{u} j \cap j >_{u} i \Rightarrow i = j\)
• 传递性：\(\forall i,j,k\in I: i >_{u} j \cap j >_{u} k \Rightarrow i >_{u} k\)

方便起见，记：

\[I^{+}_{u} = \left \{ i\in I:(u,i)\in S \right \} \]

\[U^{+}_{i} = \left \{ u\in U:(u,i)\in S \right \} \]

问题分析

现存问题

正如我们之前所指出的，在隐式反馈系统中，只观察到积极的类。其余的数据实际上是负值和缺失值的混合物。解决缺失值问题最常见的方法是忽略所有这些问题，但典型的机器学习模型无法学习任何东西，因为它们不能再区分这两个层次了。

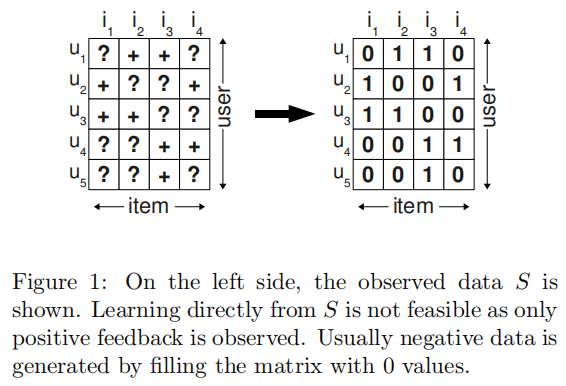
一般机器学习方法将用户和商品的交互矩阵中发生交互的用户-商品对\((u,i)\in S\)作为正样本，\((U×I)\setminus S\)中的所有其他组合作为负样本来创建训练数据（见图1）。然后对该数据进行拟合。这意味着该模型被优化，以预测S中元素的值1和其余元素的值0。这种方法的问题是，模型在未来应该排名的所有元素\((U×I)\setminus S\)在训练过程中作为负反馈呈现给学习算法。这意味着一个具有足够的表达能力（可以精确地匹配训练数据）的模型根本不能进行排名，因为它只能预测出0。这种机器学习方法能够预测排名的唯一原因是防止过拟合的策略，比如正则化。

解决办法

作者采用成对训练的方法，对于一个用户\(u\)而言，模型应该对该用户有交互的商品的预测值大于所有没有交互的商品的预测值。如图2左半部分所示，用户\(u_{1}\)和商品\(i_{2}\)、\(i_{3}\)有交互行为，则：$$pred(u_{1},i_{2}) > pred(u_{1},i_{1}) \wedge pred(u_{1},i_{2}) > pred(u_{1},i_{4})$$

\[pred(u_{1},i_{3}) > pred(u_{1},i_{1}) \wedge pred(u_{1},i_{3}) > pred(u_{1},i_{4}) \]

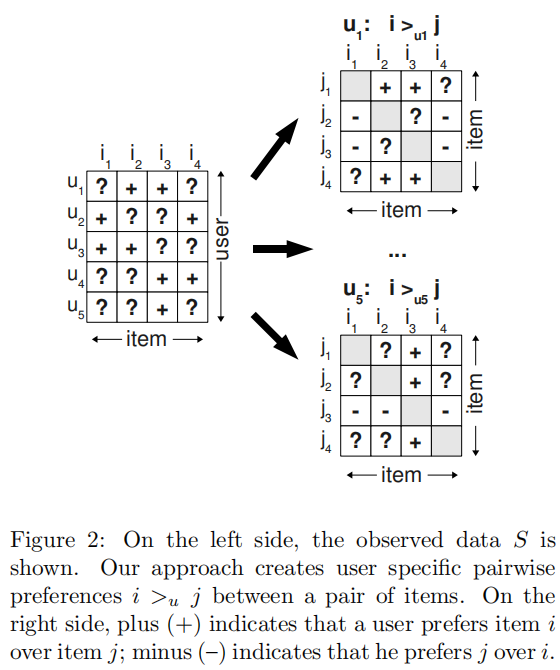
这样可以得到整体训练样本\(D_{S}:U \times I \times I\)。记为：

\[D_{s}=\left \{ (u,i,j) | i\in I^{+}_{u} \wedge j \in I \setminus I^{+}_{u} \right \} \]

\((u,i,j)\)表示相比于商品\(j\)，用户更偏向于商品\(i\)。

贝叶斯个性化排序（BPR）

优化目标

我们的目的在于已知偏序关系\(>_{u}\)的情况下，求得模型参数\(\Theta\)。BPR基于最大后验概率, 对每一个用户\(u\)而言，后验概率正比于似然概率乘上先验概率，即：

\[p(\Theta | >_{u})\propto p(>_{u} | \Theta )p(\Theta ) \]

对于所有的用户\(u \in U\)：

\[\mathop{\prod}_{u \in U} p(>_{u} | \Theta )=\mathop{\prod}_{(u,i,j) \in U \times I \times I} p(i >_{u} j | \Theta )^{\delta ((u,i,j) \in D_{S})} \cdot (1 - p(i >_{u} j | \Theta ))^{\delta ((u,i,j) \notin D_{S})} \]

其中\(\delta(\cdot)\)为指示函数。
根据反对称性，上式可写作：

\[\mathop{\prod}_{u \in U} p(>_{u} | \Theta )=\mathop{\prod}_{(u,i,j) \in D_{S}} p(i >_{u} j | \Theta) \]

令\(p(i >_{u} j | \Theta) = \sigma \left ( \hat x_{uij} \right )\)。其中\(\sigma\)为激活函数，\(\hat x_{uij}\)是模型计算出的用户的偏好值。
作者假设：

\[p(\Theta )\sim N(0,I) \]

最终的优化目标可以表示为：

\[BPR-Opt=lnp(\Theta | >_{u}) \]

\[=lnp(>_{u} | \Theta)p(\Theta) \]

\[=\sum_{(u,i,j) \in D_{S}}^{} ln \sigma (\hat x_{uij}) - \lambda _{\Theta }\left \| \Theta \right \|^{2} \]

其中\(\lambda _{\Theta }\)表示正则化参数。

如何构造负样本

对于一个用户而言，产生交互行为的商品是少量的，没有产生交互行为的商品数量是很庞大的，不可能将所有未交互的商品的当作负样本，这样数据量太大了。作者采用的方法是随机均匀采样出若干未交互商品作为负样本。

进一步分析

BPR是一个通用的框架，用户对某个商品的偏好值需要结合具体的模型（如矩阵分解、kNN）计算出来。我们以矩阵分解模型为例。

\[\hat x_{ui}=<w_{u},h_{i}>=\sum_{f=1}^{k}w_{uf}\cdot h_{if} \]

\[\hat x_{uij} = \hat x_{ui} - \hat x_{uj} \]

其中\(\hat x_{ui}\)表示模型计算出的用户\(u\)对商品\(i\)的偏好得分。易得：

\[\frac{\partial }{\partial \Theta }\hat x_{uij}=\left\{\begin{matrix} (h_{ij}-h_{jf}) & if \quad \Theta =w_{uf}\\ w_{uf} & if \quad \Theta =h_{if}\\ -w_{uf} & if \quad \Theta =h_{jf} \\ 0 & else \end{matrix}\right.\]

BPR类的实现

class BPR(nn.Module):
    def __init__(self, user_num, item_num, factor_num):
        super().__init__()
        
        self.embed_user = nn.Embedding(user_num, factor_num)
        self.embed_item = nn.Embedding(item_num, factor_num)
        
        nn.init.normal_(self.embed_user.weight, std=0.01)
        nn.init.normal_(self.embed_item.weight, std=0.01)
        
    def forward(self, user, item_i, item_j):
        user = self.embed_user(user)
        item_i = self.embed_item(item_i)
        item_j = self.embed_item(item_j)
        
        pred_i = (user * item_i).sum(dim=-1)
        pred_j = (user * item_j).sum(dim=-1)
        
        return pred_i, pred_j