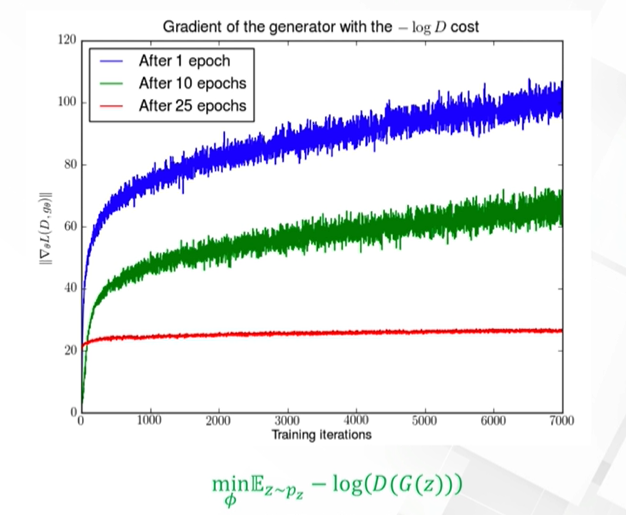
生成网络的优化目标
the -logD alternative
称生成器的目标函数:
\[\mathop{min}_{\theta } \mathbb{E}_{\boldsymbol z \sim p(\boldsymbol z)}\left [ log(1 - D \left (G (\boldsymbol z; \theta ) ;\phi \right )) \right ]
\]
为“the -logD alternative”
将GAN的目标函数写成一个统一的形式:
\[\mathop{min}_{\theta }\mathop{max}_{\phi } \mathbb{E}_{\boldsymbol x \sim p_{r}(\boldsymbol x)}\left [ logD(\boldsymbol x ;\phi ) \right ] + \mathbb{E}_{\boldsymbol z \sim p(\boldsymbol z )}\left [ log\left ( 1 - D(G(\boldsymbol z ;\theta ) ;\phi ) \right ) \right ]
\]
在生成对抗网络中,当判别网络接近最优时,生成网络的优化目标是最小化真实分布和模型分布之间的JS散度。当两个网络的分布相同时,JS散度为0,生成网络对应的损失为-2log2。在实际情况中,真实分布和模型分布有较大的重叠的可能性是微乎其微的,因此我们可以认为真实数据分布和模型的分布是不重叠的,即使重叠,那么重叠的部分也是可以忽略的,在这种情况下,两个分布之间的JS散度恒为常数log2,判别器对所有的生成数据的判定输出都为0,生成网络的损失也为0,导致生成网络无法更新(如图1所示)。
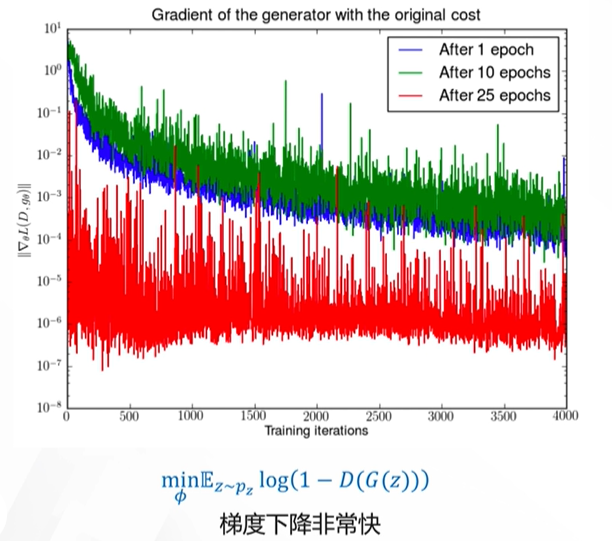

不仅如此,JS散度衡量距离还存在一个问题,从图2可以看到,只要两个分布不重叠,那么两者的JS散度都是一样的,而实际上q和r与p的距离是不一样的,JS散度无法捕捉这种差异。
the -logD trick
针对原始生成网络目标函数存在的问题,GAN之父提出了一种改进的方法,即将生成网络的目标函数修改为:
\[\mathop{min}_{\theta } \mathbb{E}_{\boldsymbol z \sim p(\boldsymbol z)}\left [- logD \left (G (\boldsymbol z; \theta ) ;\phi \right ) \right ]
\]
我们称之为“the -logD trick”。
但是这样的修改仍然存在问题,即会存在梯度不稳定(图3)和模式崩塌问题。