Thomas N.Kipf等人于2017年发表了一篇题为《SEMI_SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》的论文,提出了一种直接在图上进行卷积操作的算法,在引文网络和知识图谱的数据集中取得了state-of-the-art的效果,开启了图神经网络研究的热潮。GCN及其变体已经成功应用在自然语言处理、计算机视觉以及推荐系统中,刷新了各项任务的性能记录,GCN被认为是近几年最具价值的研究方向。本文浅谈GCN的原理,并基于自己的理解,参考了网上相关代码,实现了两层GCN,算是对GCN的一种入门吧。
节点分类问题传统做法
在一个图中(比如引文网络),图中的每个节点代表一篇论文,图中的边代表论文之间的引用关系,此外还有少量的论文有标签,即知道该部分论文所属的研究领域。节点分类任务是对所有的论文进行类别判定。传统的办法基于这样一种假设:在图中具有连边的节点应该有相似的属性,很有可能属于同一个类别。于是很自然的可以提出下面这个损失函数:
其中\(L_{0}\)是有标签部分节点的损失,\(f()\)表示一种映射关系,可以是神经网络。\(\Delta = D - A\),是节点的度矩阵与邻接矩阵的差,称为图的拉普拉斯矩阵。“在图中具有连边的节点应该有相似的属性”这一假设过于严格了,限制了图的表达能力。
GCN的做法
直接用神经网络对整个图建模,记为\(f(X,A)\),用图中有标签的那部分数据训练模型。文中的创新之处在于提出了一种逐层传播的模型,能够很方便地处理高阶邻居关系,相比于传统做法,省略了图正则化部分,使的模型更具灵活性,表达能力更强。在这里直接给出图卷积的公式:
式中:
- \(\tilde A = A + I\),\(A\)表示邻接矩阵,维度为\(N \times N\),\(N\)为节点数量,\(I\)表示和\(A\)维度相同的单位矩阵。
- \(\tilde D = D + I\),\(D\)表示度矩阵,维度为\(N \times N\)。
- \(H^{(l)}\)表示第\(l\)层各节点的特征,\(H^{(0)}\)表示原始节点特征的矩阵。
- \(W^{(l)}\)表示第\(l\)可学习的参数。
- \(\tilde D^{-\frac{1}{2}} \tilde A \tilde D^{-\frac{1}{2}}\)表示对矩阵\(\tilde A\)进行归一化,避免邻居数量越多,卷积后结果越大的情况以及考虑了邻居的度大小对卷积的影响。
- \(\sigma()\)表示激活函数。
半监督学习框架
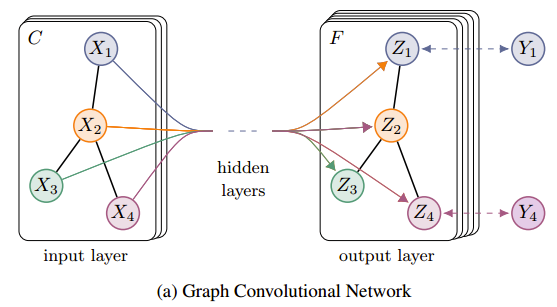
假设输入节点有四个,分别是\(X_{1}\),\(X_{2}\),\(X_{3}\),\(X_{3}\),每个节点的特征向量的维度是\(C\),其中节点\(X_{1}\)和\(X_{4}\)是带标签的,节点\(X_{2}\)和\(X_{3}\)是不带标签的,经过多层的卷积操作之后,四个节点的特征向量维度都变成了\(F\)。利用图中有标签的节点计算损失函数,对GCN中的参数进行训练。
两层GCN示例
第一层图卷积:
第二层图卷积:
参数训练:
图中的所有节点中有一部分节点是带标签的,因此我们可以利用这部分带标签的节点的类别,计算真实类别与预测类别的损失函数,从而优化GCN参数。损失函数定义如下:
其中\(y_{L}\),是有标签的节点集合,\(F\)是节点最终特征向量的维度。
cora数据集介绍
1 下载地址https://linqs.soe.ucsc.edu/data
2 文件构成
cora数据集包含了机器学习相关的论文,论文的类别有七种,分别是:
- Case_Based
- Genetic_Algorithms
- Neural_Networks
- Probabilistic_Methods
- Reinforcement_Learning
- Rule_Learning
- Theory
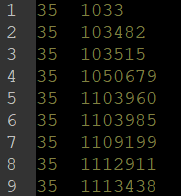
cora数据集共包含两个文件。其中.content文件的每一行代表一篇论文,每行的组织形式是:<paper_id> <word_attributes> <class_label>。word_attributes是维度为1433的one-hot向量,class_label是上述七种类型的一种。
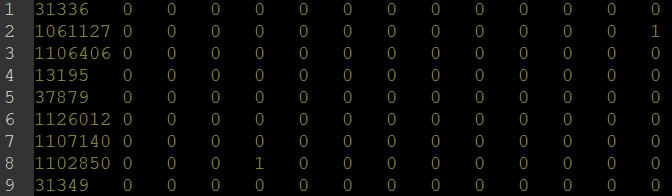
.cites文件记录了论文之间的引用关系。文件的每一行代表
代码
import numpy as np
import scipy.sparse as sp
import torch
import math
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
def encode_onehot(labels):
classes = set(labels)
class_dict = {c: np.identity(len(classes))[i, :] for i, c in enumerate(classes)}
label_onehot = np.array(list(map(class_dict.get, labels)),
dtype=np.int32)
return label_onehot
def normalize(mx):
rowsum = np.array(mx.sum(1))
r_inv = np.power(rowsum, -1).flatten()
r_inv[np.isinf(r_inv)] = 0
r_mat_inv = sp.diags(r_inv)
mx = r_mat_inv.dot(mx)
return mx
def accuracy(output, labels):
pred = output.max(1)[1].type_as(labels)
correct = pred.eq(labels).double()
correct = correct.sum()
return correct / len(labels)
def sparse_mx_to_torch_sparse_tensor(sparse_mx):
sparse_mx = sparse_mx.tocoo().astype(np.float32)
indices = torch.from_numpy(
np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
values = torch.from_numpy(sparse_mx.data)
shape = torch.Size(sparse_mx.shape)
return torch.sparse.FloatTensor(indices, values, shape)
def load_data(path="C:/Users/DZL102/Downloads/cora/", dataset="cora"):
print("Loading data...")
idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
dtype=np.dtype(str))
features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
labels = encode_onehot(idx_features_labels[:, -1])
# build graph
idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
idx_map = {j: i for i, j in enumerate(idx)}
edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
dtype=np.int32)
edges = np.array(list(map(idx_map.get, edges_unordered.flatten())), dtype=np.int32,
).reshape(edges_unordered.shape)
adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
shape=(labels.shape[0], labels.shape[0]),
dtype=np.float32)
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
features = normalize(features)
adj = normalize(adj + sp.eye(adj.shape[0]))
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)
features = torch.FloatTensor(np.array(features.todense()))
labels = torch.LongTensor(np.where(labels)[1])
adj = sparse_mx_to_torch_sparse_tensor(adj)
idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
idx_test = torch.LongTensor(idx_test)
print("数据加载成功...")
return adj, features, labels, idx_train, idx_val, idx_test
class GraphConvolution(nn.Module):
def __init__(self, in_features, out_features, bias=True):
super(GraphConvolution, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = nn.Parameter(torch.FloatTensor(in_features, out_features))
self.use_bias = bias
if self.use_bias:
self.bias = nn.Parameter(torch.FloatTensor(out_features))
self.reset_parameters()
def reset_parameters(self):
nn.init.kaiming_uniform_(self.weight)
if self.use_bias:
nn.init.zeros_(self.bias)
def forward(self, input_features, adj):
support = torch.mm(input_features, self.weight)
output = torch.spmm(adj, support)
if self.use_bias:
return output + self.bias
else:
return output
class GCN(nn.Module):
def __init__(self, input_dim=1433):
super(GCN, self).__init__()
self.gcn1 = GraphConvolution(input_dim, 16)
self.gcn2 = GraphConvolution(16, 7)
pass
def forward(self, X, adj):
X = F.relu(self.gcn1(X, adj))
X = self.gcn2(X, adj)
return F.log_softmax(X, dim=1)
model = GCN(features.shape[1])
optimizer = optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
def train(epochs):
for epoch in range(epochs):
optimizer.zero_grad()
output = model(features, adj)
loss_train = F.nll_loss(output[idx_train], labels[idx_train])
acc_train = accuracy(output[idx_train], labels[idx_train])
loss_train.backward()
optimizer.step()
loss_val = F.nll_loss(output[idx_val], labels[idx_val])
acc_val = accuracy(output[idx_val], labels[idx_val])
if (epoch % 10 == 0):
print("Epoch: {}".format(epoch + 1),
"loss_train: {:.4f}".format(loss_train.item()),
"acc_train: {:.4f}".format(acc_train.item()),
"loss_val: {:.4f}".format(loss_val.item()),
"acc_val: {:.4f}".format(acc_val.item()))
if __name__ == "__main__":
train(200)
运行结果
Epoch: 1 loss_train: 1.9277 acc_train: 0.1429 loss_val: 1.9348 acc_val: 0.1100
Epoch: 11 loss_train: 1.7104 acc_train: 0.4286 loss_val: 1.7408 acc_val: 0.4267
Epoch: 21 loss_train: 1.4866 acc_train: 0.5714 loss_val: 1.5790 acc_val: 0.5267
Epoch: 31 loss_train: 1.2659 acc_train: 0.6071 loss_val: 1.4243 acc_val: 0.5700
Epoch: 41 loss_train: 1.0554 acc_train: 0.7286 loss_val: 1.2715 acc_val: 0.6233
Epoch: 51 loss_train: 0.8724 acc_train: 0.8357 loss_val: 1.1299 acc_val: 0.7000
Epoch: 61 loss_train: 0.7206 acc_train: 0.8786 loss_val: 1.0145 acc_val: 0.7567
Epoch: 71 loss_train: 0.6001 acc_train: 0.9286 loss_val: 0.9232 acc_val: 0.7767
Epoch: 81 loss_train: 0.5080 acc_train: 0.9429 loss_val: 0.8550 acc_val: 0.7933
Epoch: 91 loss_train: 0.4396 acc_train: 0.9643 loss_val: 0.8056 acc_val: 0.8033
Epoch: 101 loss_train: 0.3885 acc_train: 0.9714 loss_val: 0.7692 acc_val: 0.8067
Epoch: 111 loss_train: 0.3500 acc_train: 0.9714 loss_val: 0.7428 acc_val: 0.8100
Epoch: 121 loss_train: 0.3203 acc_train: 0.9714 loss_val: 0.7234 acc_val: 0.8100
Epoch: 131 loss_train: 0.2968 acc_train: 0.9714 loss_val: 0.7085 acc_val: 0.8133
Epoch: 141 loss_train: 0.2778 acc_train: 0.9714 loss_val: 0.6971 acc_val: 0.8033
Epoch: 151 loss_train: 0.2621 acc_train: 0.9786 loss_val: 0.6881 acc_val: 0.8067
Epoch: 161 loss_train: 0.2489 acc_train: 0.9786 loss_val: 0.6808 acc_val: 0.8167
Epoch: 171 loss_train: 0.2376 acc_train: 0.9786 loss_val: 0.6748 acc_val: 0.8133
Epoch: 181 loss_train: 0.2278 acc_train: 0.9857 loss_val: 0.6700 acc_val: 0.8133
Epoch: 191 loss_train: 0.2193 acc_train: 0.9929 loss_val: 0.6659 acc_val: 0.8100


 浙公网安备 33010602011771号
浙公网安备 33010602011771号