机器学习常用损失函数

机器学习三要素——模型、学习准则、优化算法。其中学习准则可以简单理解为损失函数，优化算法就是用来优化损失函数的。根据任务不同，损失函数可以分为回归损失函数和分类损失函数，每种类别的损失函数有很多种，不同的损失函数的形式以及出发点都不同，在实际应用中，根据任务的需要，选取合适的损失函数是非常关键的，它直接决定了最终模型的好坏。本文将损失函数\(L\)与代价函数\(J\)区分开来，损失函数代表一个样本的损失，代价函数代表整体样本的损失，在用梯度下降算法优化时，优化的是代价函数，代价函数是损失函数在整体样本上损失和的平均。

分类问题的损失函数

0-1损失

最直观的损失函数就是0-1损失函数，如果样本被分类正确，则损失为0，否则损失为1。

\[L(y,f(\boldsymbol{x};\theta ))=\left\{\begin{matrix} 0 \quad if \ y=f(\boldsymbol{x};\theta )\\ 1 \quad otherwise \end{matrix}\right.\]

虽然0-1损失函数能够客观刻画模型的好坏，但是它不连续且导数为0，难以优化。

交叉熵损失

假设样本的标签\(y\in \left \{ 1,2,...,C \right \}\)为离散的类别，模型\(f(\boldsymbol{x};\theta ) \in [0,1]^{C}\)的输出为类别标签的条件概率分布，即：

\[p(y=c|\boldsymbol{x}; \theta )=f_{c}(\boldsymbol{x}; \theta) \]

并且满足：

\[f_{c}(\boldsymbol{x}; \theta) \in [0,1], \quad \sum_{c=1}^{C}f_{c}(\boldsymbol{x };\theta)=1 \]

用一个\(C\)维的one-hot向量\(\boldsymbol{y}\)来表示样本标签。假设样本标签为\(k\)，那么\(\boldsymbol{y}\)中有第\(k\)维的值为1，其余元素的值为0。向量\(\boldsymbol{y}\)可以看作样本标签的真实条件概率分布。对于两个概率分布，一般可用交叉熵来衡量它们之间的差异。标签的真实分布\(\boldsymbol{y}\)和模型的预测分布\(f(\boldsymbol{x};\theta )\)之间的交叉熵为：

\[L(\boldsymbol{y},f(\boldsymbol{x};\theta ))=-\boldsymbol{y}^{T}logf(\boldsymbol{x};\theta ) \]

\[=-\sum_{c=1}^{C}y_{c}logf_{c}(\boldsymbol{x};\theta) \]

特别地，当问题是二分类问题，交叉熵损失可写作（如逻辑回归问题）：

\[L(y,f(\boldsymbol{x};\theta ))=-[ylogf(\boldsymbol{x};\theta )+(1-y)log(1-f(\boldsymbol{x};\theta ))] \]

Hinge损失

对于二分类问题，假设\(y\)的取值为\(\left \{ -1,1 \right \}\)，\(f(\boldsymbol{x};\theta )\in \mathbb{R}\)，Hinge损失函数为：

\[L(y,f(\boldsymbol{x};\theta ))=max(0,1-yf(\boldsymbol{x};\theta )) \]

SVM中的损失函数就是Hinge损失。

指数损失

指数损失函数的公式为：

\[L(y,f(\boldsymbol{x};\theta ))=exp(-yf(\boldsymbol{x};\theta )) \]

指数损失与交叉熵损失类似，但它是指数下降的，因此梯度较其它损失来说，更大一些。指数损失一般多用于AdaBoost中。因为使用指数损失能比较方便地利用加法模型推导出AdaBoost算法。该损失函数对异常点较为敏感，相对于其他损失函数鲁棒性较差。

Softmax损失

是softmax和交叉熵损失组合而成的损失函数。先来看看什么是softmax。
假设模型的输出为一个向量：

\[\begin{bmatrix} \hat y_{1}\\ \hat y_{2}\\ \hat y_{3}\\ \vdots \\ \hat y_{C} \end{bmatrix}\]

向量的每一维的值可能是任意的，实际上我们希望向量的每一维都在0~1之间，表示属于某一类的概率。想要达到这一目的，只需要对输出向量做softmax处理：

\[\hat y_{j}=\frac{e^{\hat y_{j}}}{\sum_{i=1}^{C}e^{\hat y_{i}}} \]

softmax损失就是对处理完的向量做交叉熵损失处理：

\[L(\boldsymbol{y}, \boldsymbol{\hat y})=-\sum_{i=1}^{C}\boldsymbol{y}_{i}log\boldsymbol {\hat y}_{i} \]

回归问题的损失函数

均方误差（MSE）

均方误差损失又叫做L2损失，是真实值与预测值差值的平方的总和的平均值。

\[L(y, \hat y)=(y- \hat y)^{2} \]

\[J=\frac{1}{2m} \sum_{i=1}^{m}(y_{i}- \hat y_{i})^2 \]

代价函数一般会再乘以二分之一，这样求导时可以抵消。

均方根误差（RMSE）

就是对MSE开根号：

\[J=\sqrt{\frac{1}{2m} \sum_{i=1}^{m}(y_{i}- \hat y_{i})^2} \]

RMSE与MAE的量纲相同。

平均绝对误差（MAE）

平均绝对误差损失又叫做L1损失，是目标值与预测值之间差的绝对值的总和的平均值。

\[L(y, \hat y)=\left | y_{i} - \hat y_{i} \right | \]

\[J=\frac{1}{m} \sum_{i=1}^{m}\left | y_{i} - \hat y_{i} \right | \]

MSE与MAE的比较

• MSE数学性质更好，更容易优化。但是MAE鲁棒性更强。
• MSE对误差取了平方（令e=真实值-预测值），因此若e>1，则MSE会进一步增大误差。如果数据中存在异常点，那么e值就会很大，而e则会远大于|e|。因此，相对于使用MAE计算损失，使用MSE的模型会赋予异常点更大的权重。用RMSE计算损失的模型会以牺牲了其他样本的误差为代价，朝着减小异常点误差的方向更新。然而这会降低模型的整体性能。如果训练数据被异常点所污染，那么MAE损失就更好（比如，在训练数据中存在大量错误的反例和正例标记，但是在测试集中没有这个问题）。
• 直观上可以这样理解：如果我们最小化MSE来对所有的样本点只给出一个预测值，那么这个值一定是所有目标值的平均值。但如果是最小化MAE，那么这个值，则会是所有样本点目标值的中位数。众所周知，对异常值而言，中位数比均值更加鲁棒，因此MAE对于异常值也比MSE更稳定。
• MAE存在一个严重的问题（特别是对于神经网络）：更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大。这样不利于模型的学习。为了解决这个缺陷，我们可以使用变化的学习率，在损失接近最小值时降低学习率。而MSE在这种情况下的表现就很好，即便使用固定的学习率也可以有效收敛。MSE损失的梯度随损失增大而增大，而损失趋于0时则会减小。这使得在训练结束时，使用MSE模型的结果会更精确。

如何选择

• 如果异常值对业务很重要，我们需要将它识别出来，那么应该使用MSE，另一方面，如果我们认为异常值只是代表无用的数据，那么我们应该选择MAE作为损失函数。

MAE与MSE都存在的问题

• 在某些情况下，两种损失函数都不能给出令人满意的预测。例如，如果我们数据中90%的观测值的目标值时150，其余10%的目标值在0到30之间。然后，一个以MAE作为损失的模型预测所有观测值为150，忽略10%的异常情况，因为该模型的作用接近于中值算法。同样的情况下，使用MSE的模型会给出许多0~30范围内的预测，因为它会向异常值倾斜。在许多业务案例中，这两个结果都是不受欢迎的。

Huber损失，平滑平均绝对误差（Smooth Mean Absolute Error）

Huber损失综合考虑了MAE和MSE的优点，对数据中的异常值不那么敏感，当误差很小时就变成了MSE，当误差很大时就变成了MAE。

\[L_{\delta }(y,\hat y)=\left\{\begin{matrix} \frac{1}{2}(y- \hat y)^{2} \quad for \ \left | y- \hat y \right |\leqslant \delta, \\ \delta \left | y- \hat y \right |-\frac{1}{2}\delta ^{2} \quad otherwise. \end{matrix}\right.\]

\(\theta\)是可调的参数，当\(\delta \rightarrow 0\)时，Huber损失接近MAE；当\(\delta \rightarrow \infty\)时，Huber接近MSE。下图为Huber函数图像，不同颜色的线表示不同的超参数。

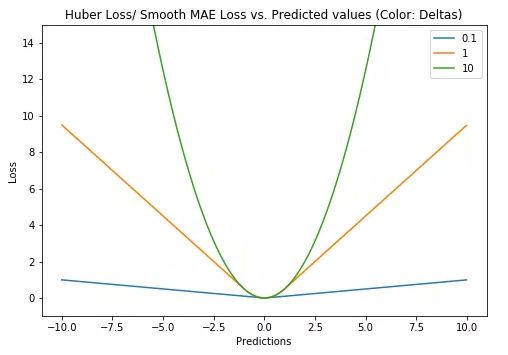
Huber的优点

MAE更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大。这样不利于模型的学习。Huber损失在这种情况下是很有帮助的，因为它在最小值附近减小了梯度，而且比MSE更健壮。因此，Huber损失结合了MSE和MAE的优点。

Huber的缺点

有个超参数\(\delta\)需要调节

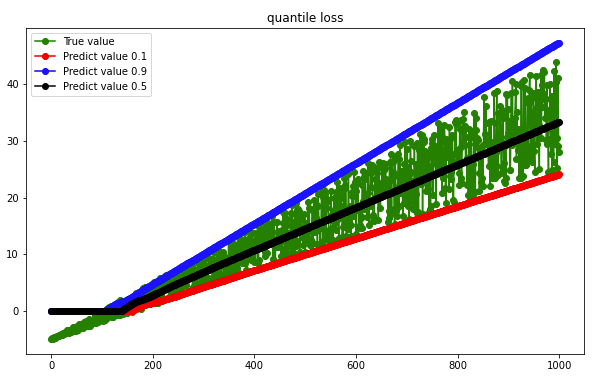
分位数损失（quantile loss）

分位数损失函数控制预测的值偏向哪个区间，当分位数是0.5时，分位数损失就是MAE。公式如下：

\[L_{\gamma }(y,y^{p})=\sum_{i=y_{i}<y_{i}^{p}}^{}(\gamma -1)\cdot \left | y_{i}-y_{i}^{p} \right |+\sum_{i=y_{i}\geq y_{i}^{p}}^{}(\gamma)\cdot \left | y_{i}-y_{i}^{p} \right | \]

蓝色：0.9分位数；黑色：中位数；红色：0.1分位数

参考

1. 如何选择回归损失：MAE还是MSE？
2. 分位数损失函数（quantile loss）