Logistic回归

导读

逻辑回归（LR）是一种分类模型，一般用于解决二分类问题，当然也可以扩展到多分类问题上。为什么要引入逻辑回归来解决分类问题呢？因为线性模型如果用于分类问题会有很大的问题。

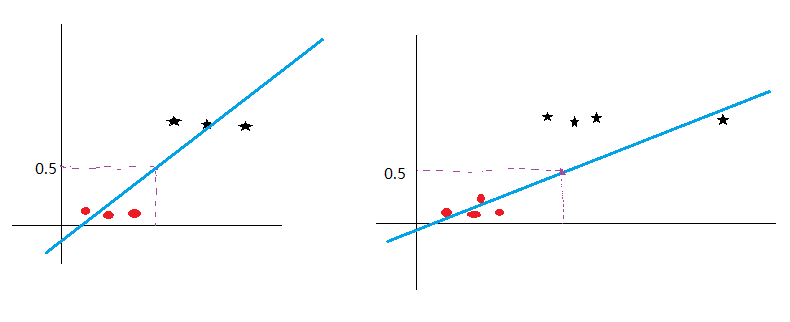
如上图所示，对于左边一幅图，我们用线性模型去拟合，并规定超过阈值0.5的为一类，小于0.5的为另一类，可以很好地将两类区分开来。但是假设有另一个样本，离其他样本的距离很远，但我们明确知道其属于星状的那一刻类，再用线性模型进行拟合的话，将如右图所示，此时再选取0.5作为阈值显然是不合适的。此外对于某些类型的数据，如数据在平面上分布呈长方形/正方形等，由于线性模型损失函数的缘故，有时根本无法将这样的数据分布用一条线区分开来（因为同时要保证点离直线的距离之和要尽可能的小，与感知机区分开来）。二分类问题的样本标签取值一般为0或1，需要找到一种函数，将线性模型的运算结果映射到（0， 1）之间，一种可选的方式是采用跃阶函数，即大于零的判断为正例，小于零的判断为负例。但由于跃阶函数不连续，无法求导，因此常用对数几率函数代替跃阶函数，对数几率函数在形状上与跃阶函数较为相似，但处处可导，优化起来比较方便。

建模

假设线性模型的输出为：

\[z=wx+b \]

将\(z\)带入到对数几率函数中有：

\[y=\frac{1}{1+e^{-y}}=\frac{1}{1+e^{-(wx+b)}} \]

称上式为给定样本\(x\)的条件下，其标签被预测为正例（设正例为1）的概率。

要想优化参数\(w\)和\(b\)，我们需要建立一个损失函数，LR中采用的损失函数是交叉熵损失函数，下面从极大似然估计的角度推导交叉熵损失。对于\(m\)个样本\(\left \{ x_{i},y_{i} \right \}^{m}_{i=1}\)，易知最大似然函数为：

\[C=\prod_{i=1}^{m}p(y_{i}|x_{i};w,b) \]

\[=\prod_{i=1}^{m}p(\hat y_{i}=1|x_{i};w,b)^{y_{i}}p(\hat y_{i}=0|x_{i};w,b)^{1-y_{i}} \]

我们的目标便是最大化上述似然函数，首先对似然函数两边取自然对数：

\[L=lnC=\sum_{i=1}^{m}y_{i}\cdot p(\hat y_{i}=1)+(1-y_{i})\cdot p(\hat y_{i}=0) \]

\[=\sum_{i=1}^{m}y_{i}\cdot log \hat y_{i}+(1-y_{i})\cdot log (1-\hat y_{i}) \]

最大化\(L\)即最小化\(-L\)，于是最终的损失函数转化为：

\[L=-\sum_{i=1}^{m}y_{i}\cdot log \hat y_{i}+(1-y_{i})\cdot log (1-\hat y_{i}) \]

用梯度下降法求解即可。

与其他模型的对比

与线性回归模型的对比

逻辑回归是对线性回归模型的结果加了一个sigmoid映射，使得结果都在0~1之间，使模型更加适应于分类问题。线性回归模型解决的是回归预测问题。

与最大熵模型

逻辑回归的损失函数可以用最大似然推导出来，因此可以说逻辑回归是最大熵模型解决二分类问题的一个特例。

与SVM

（1）相同点

• 都是分类算法
• 都是判别式模型

（2）不同点

• SVM 的处理方法是只考虑 Support Vectors，也就是和分类最相关的少数点去学习分类器。而逻辑回归通过非线性映射减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。
• 损失函数不同：LR 的损失函数是交叉熵，SVM 的损失函数是 HingeLoss，这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。对
  HingeLoss 来说，其零区域对应的正是非支持向量的普通样本，从而所有的普通样本都不参与最终超平面的决定，这是支持向量机最大的优势所在，对训练样本数目的依赖大减少，而且提高了训练效率。
• LR 是参数模型，SVM 是非参数模型，参数模型的前提是假设数据服从某一分布，该分布由一些参数确定（比如正太分布由均值和方差确定），在此基础上构建的模型称为参数模型；
  非参数模型对于总体的分布不做任何假设，只是知道总体是一个随机变量，其分布是存在的（分布中也可能存在参数），但是无法知道其分布的形式，更不知道分布的相关参数，只有在给定一些样本的条件下，能够依据非参数统计的方法进行推断。所以 LR 受数据分布影响，尤其是样本不均衡时影响很大，需要先做平衡，而 SVM 不直接依赖于分布；
• LR 相对来说模型更简单好理解，特别是大规模线性分类时并行计算比较方便。而 SVM 的理解和优化相对来说复杂一些，SVM 转化为对偶问题后，分类只需要计算与少数几个支持向
  量的距离，这个在进行复杂核函数计算时优势很明显，能够大大简化模型和计算。
• LR 不依赖样本之间的距离，SVM 是基于距离的。

补充

用LR建模为什么要对特征离散化

在工业界，很少直接将连续值作为特征喂给逻辑回归模型，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：

• 稀疏向量内积乘法运算速度快，计算结果方便存储，容易scalable（扩展）。
• 离散化后的特征对异常数据有很强的鲁棒性：（1）特征敏感性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰。（2）：大小比较不一致性：从10增加到20和从20增加到30对模型的影响不一定一样。
• 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合。
• 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力。
• 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问。李沐少帅指出，模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以n个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。

怎么进行离散化

（1）手动分组：统计每个组的情况
（2）自动分组：GBDT+LR
先来看看如何进行特征组合：
我们可以根据人对业务的理解，手动进行特征组合，产生二阶、三阶甚至更高阶的特征。但当特征数目比较大时，很难进行人工特征组合，且不确定组合出的特征是否对模型有帮助。因此需要用模型帮助我们进行特征组合。

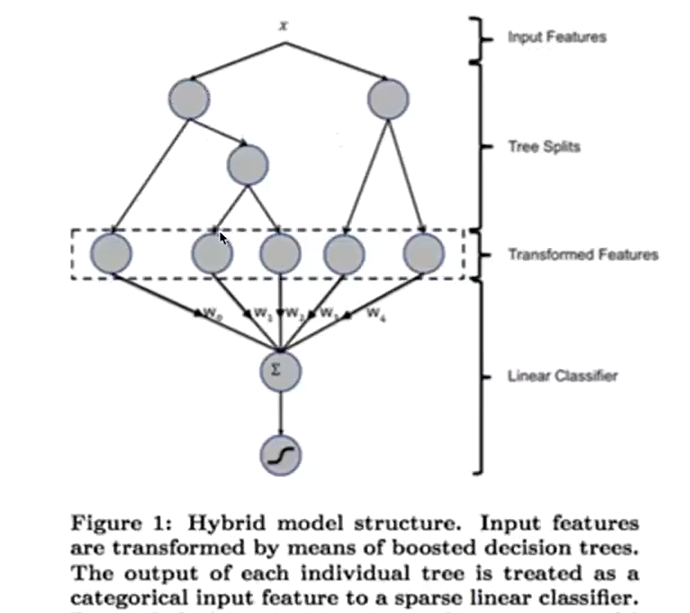
损失函数为什么不用平方损失

（1）从参数更新的角度

\[z_{i}=wx_{i}+b \]

\[\hat y_{i}=\sigma(z_{i})，\sigma 为sigmoid函数 \]

考虑平方损失：

\[L=\frac{1}{m}\sum_{i=1}^{m}(\hat y_{i}-y_{i})^{2} \]

对参数\(w\)和\(b\)求导得：

\[w^{'}=\frac{2}{m} \sum_{i=1}^{m}(\hat y_{i}-y_{i})\sigma ^{'}(z_{i})x_{i} \]

\[b^{'}=\frac{2}{m} \sum_{i=1}^{m}(\hat y_{i}-y_{i})\sigma ^{'}(z_{i}) \]

可以看出当\(z\)过大或者过小的时候\(\sigma ^{'}(z_{i})\)趋近于0，从而导致参数更新太慢。

考虑交叉熵损失：

\[w^{'}=\frac{1}{m} \sum_{i=1}^{m}(\hat y_{i}-y_{i})x_{i} \]

\[b^{'}=\frac{1}{m} \sum_{i=1}^{m}(\hat y_{i}-y_{i}) \]

可以看出，采用交叉熵损失函数，参数梯度不包含\(\sigma ^{'}(z_{i})\)项，与\(\hat y_{i}-y_{i}\)有关，当误差小的时候参数更新幅度小，当误差大的时候参数更新幅度大，符合梯度下降法的要求。

（2）从损失函数特性的角度
我们用梯度下降法优化目标函数时，如果目标函数是非凸的，则有可能陷入局部极小值点。如果一个函数的二阶导数是恒不小于0的，则称此函数为凸函数，很明显平方损失函数的二阶导数不恒不小于0，是个非凸函数。相反，交叉熵损失函数是凸函数。

参考

1. 【机器学习】逻辑回归（非常详细）
2. LR为什么要对特征进行离散化处理