FM（因子分解机）原理与实战

0 概述

因子分解机（Factorization Machine，FM）于2010年被首次提出，其目的是解决数据稀疏问题以及特征组合爆炸问题，是曾经火爆学术界的推荐模型，虽然近几年基于深度学习的推荐算法是众多学者的研究热点，但因FM实现简单，效果强大，其思想仍值得我们深入研究。此外FM与深度学习技术的结合，使推荐效果得到了更好地提升。首先了解一下POLY2模型，其公式如下：

\[\varnothing POLY2(\boldsymbol{w},\boldsymbol{x})=\sum_{j_{1}=1}^{n-1}\sum_{j_{2}=j_{1}+1}^{n}w_{h(j_{1},j_{2})}x_{j_{1}}x_{j_{2}} \]

式中\(w_{h(j_{1},j_{2})}\)是特征\(x_{j_{1}}\)和特征\(x_{j_{2}}\)的交叉的权重，是待学习的参数。在推荐系统领域中，特征通常是one-hot编码，维度非常大且十分稀疏，POLY2模型有两个缺点：一是需要考虑所有特征的两两组合的情况，参数的数量达到\(O(n^{2})\)级；二是只有当\(x_{j_{1}}\)和\(x_{j_{2}}\)都不为0时\(w_{h(j_{1},j_{2})}\)才能的到更新，但在数据稀疏的情况下很难得到满足。为了解决上述两种问题，FM的解决方式是用两个向量的内积\(<v_{j_{1}},v_{j_{2}}>\)代替单一的权重系数。也就是说FM模型为每个特征都学习一个向量表示（向量的维度是超参数，可自定义），两个特征的交叉的权重就是这两个特征对应的向量表示的内积。FM模型可用数学公式述为：

\[\varnothing FM(\boldsymbol{w},\boldsymbol{x})=w_{0}+\sum_{i=1}^{n}w_{i}x_{i}+\sum_{j_{1}=1}^{n-1}\sum_{j_{2}=j_{1}+1}^{n}<v_{j_{1}},v_{j_{2}}>x_{j_{1}}x_{j_{2}} \]

1 进一步推导

FM模型的前半部分是线性模型，比较简单，因此本节着重对后半部分二阶特征交叉项作进一步推导，最后给出矩阵实现。不妨假设特征维度为\(n\)，样本数量为\(m\)，因子数量（每个特征对应的向量维度）为\(k\)。用\(X\)代表样本，用\(V\)代表需要学习的因子。其中：

\[X=\begin{bmatrix} \boldsymbol{x^{1}} & \boldsymbol{x^{2}} & \cdots & \boldsymbol{x^{m}} \end{bmatrix} =\begin{bmatrix} x^{1}_{1} & x^{2}_{1} & \cdots & x^{m}_{1}\\ x^{1}_{2} & x^{2}_{2} & \cdots & x^{m}_{2}\\ \vdots & \vdots & \vdots & \vdots \\ x^{1}_{n} & x^{2}_{n} & \cdots & x^{m}_{n} \end{bmatrix}\]

\[V=\begin{bmatrix} \boldsymbol{v^{1}}\\ \boldsymbol{v^{2}}\\ \vdots \\ \boldsymbol{v^{n}} \end{bmatrix} =\begin{bmatrix} v^{1}_{1} & v^{1}_{2} & \cdots & v^{1}_{k}\\ v^{2}_{1} & v^{2}_{2} & \cdots & v^{2}_{k}\\ \vdots & \vdots & \vdots & \vdots \\ v^{n}_{1} & v^{n}_{2} & \cdots & v^{n}_{k} \end{bmatrix}\]

于是：

\[\sum_{j_{1}=1}^{n-1}\sum_{j_{2}=j_{1}+1}^{n}<v_{j_{1}},v_{j_{2}}>x_{j_{1}}x_{j_{2}} \]

\[=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}<v_{i},v_{j}>x_{i}x_{j}-\frac{1}{2}\sum_{i=1}^{n}<v_{i},v_{i}>x_{i}x_{i} \]

\[=\frac{1}{2}(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k}v_{i,f}*v_{j,f}*x_{i}x_{j}-\sum_{i=1}^{n}\sum_{f=1}^{k}v_{i,f}*v_{i,f}*x_{i}x_{i}) \]

\[=\frac{1}{2}\sum_{f=1}^{k}(\sum_{i=1}^{n}\sum_{j=1}^{n}v_{i,f}*v_{j,f}*x_{i}x_{j}-\sum_{i=1}^{n}v_{i,f}*v_{i,f}*x_{i}x_{i}) \]

\[=\frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}v_{i,f}*x_{i})(\sum_{j=1}^{n}v_{j,f}*x_{j})-\sum_{i=1}^{n}v_{i,f}^{2}*x_{i}^{2}) \]

\[=\frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}v_{i,f}*x_{i})^{2}-\sum_{i=1}^{n}v_{i,f}^{2}*x_{i}^{2})) \]

写成矩阵的形式：

\[\varnothing FM(\boldsymbol{W},\boldsymbol{V},\boldsymbol{X})=W^{'}\cdot X^{'}\cdot \boldsymbol{I}_{m\times 1}+\boldsymbol{I}_{1\times k}\cdot [(V^{T}\cdot X)^{2}-(V^{T})^{2}\cdot X^{2}]\cdot \boldsymbol{I}_{m\times 1} \]

其中加号左边为线性部分\(X^{'}\)是\(X\)的增广形式，加号的后半部分为二阶特征交叉部分

2 基于pytorch实现

本节将利用深度学习框架pytorch实现FM算法，数据集选用MovieLens-1M。

2.1 文件结构

从上到下文件的含义为：

• data_process.py 数据预处理文件，原始数据集包含三种文件（分别是user、movie、rating文件）需要以rating文件为依据，将rating文件的每一行拼接上用户的特征、电影的特征。在处理类别型数据时采用one-hot编码，对模型训练没有帮助的特征（如邮政编码、时间戳等）直接删除。
• fm.py 矩阵分解模型实现的代码包含在此文件中。
• movies.dat 存储了所有的电影信息
• orig_data.csv 数据如处理后产生的最终用于训练模型的数据，先存在一个文件中，方便后续使用
• rating.dat 存储了用户对电影的评分
• test_data.csv 用于测试的数据集
• train_data.csv 用于训练的数据集
• user.dat 存储了用户相关信息

2.2 主要代码段

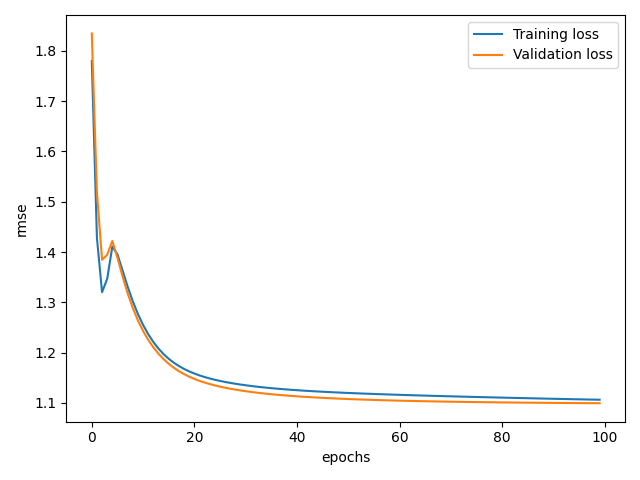
完整代码已上传到github，请点击点击这里下载。训练100个epoch，训练集和测试集误差如下图所示：

FM模型的实现如下：

class FM(nn.Module):
    def __init__(self, n, k):
        super(FM, self).__init__()
        self.n = n  # 特征数
        self.k = k  # 因子数
        self.linear_part = nn.Linear(self.n, 1, bias=True)
        self.v = nn.Parameter(torch.rand(self.k, self.n))

    def fm(self, x):
        linear_part = self.linear_part(x)
        cross_part1 = torch.mm(x, self.v.t())
        cross_part2 = torch.mm(torch.pow(x, 2), torch.pow(self.v, 2).t())
        cross_part = torch.sum(torch.sub(torch.pow(cross_part1, 2), cross_part2), dim=1)
        output = linear_part.transpose(1, 0) + 0.5 * cross_part

        return output

    def forward(self, x):
        output = self.fm(x)
        return output

3 FM为什么能缓解数据稀疏性问题

这里引用《深度学习推荐系统》————王喆著里面的解释
假设在某推荐场景下，样本有两个特征，分别是频道（channel）和品牌（brand），某训练样本的特征组合是(ESPN, Adidas)。在POLY2中，只有当ESPN和Adidas同时出现在一个样本中时，模型才能学到这两个特征组合对应的权重；而在FM模型中，ESPN的隐向量可以通过(ESPN, Gucci)来更新，Adidas的隐向量也可以通过(NBC, Adidas)来更新，这大幅降低了模型对数据稀疏性的要求。